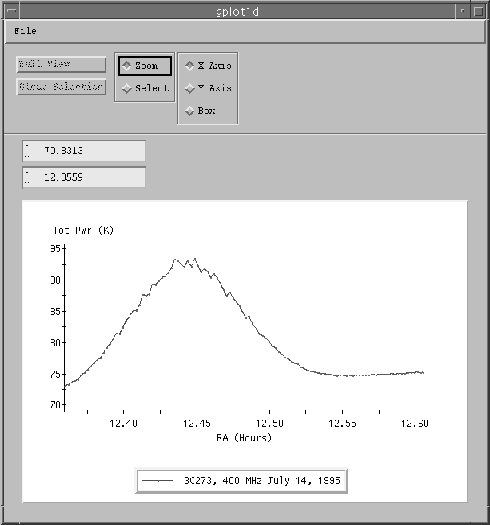
We start with the first source scan obtained. This was taken at 1:30 UT on July 14, 1995 using the 140-ft under GBT Monitor & Control, the new GBT Digital Continuum Receiver, and AIPS++. There was no fudging on the plot except to tell Glish the value of cal temperature and doing the data operations line by line in Glish.
Next we describe some of the data and show how Glish is used to manipulate the data and produce plots. The names ending in .fits are FITS format data files written by the M&C system. The commands like PlotTPcCE1 are Glish commands written specially (for a description of Glish capabilities, see the Glish manual). The plots are screen-dumps of the output from the Glish plotting client (gplot1d), in postscript format. Rick Fisher gives the following commentary:
Tipping scan from Elev = 15 to 90 degrees, az = 0 (south) 1995_07_19_13:16:09_Dcr.fits plotTPwCEl(1.6, table, 8, 1|2) or plotTPwCSecZ(1.6, table, 8, 1|2) One normally solves for the slope and intercept of a straight line fit to the T vs sec(z) data with obvious bumps and data at (sec(z) < 1.05) edited out. The curve is not a straight line, so a more sophisticated analysis would remove known spillover effects from the data before fitting and possibly use a non-planar atmosphere model. See the fitTipping() function in rfUtils.g
R.A. scan map of 3c273. Nine scans at 10' intervals from +40' to -40' around the source declination. Each scan was 90'/cos(dec) wide. 1995_07_19_00:17:23_Dcr.fits 1995_07_19_00:19:23_Dcr.fits 1995_07_19_00:21:21_Dcr.fits 1995_07_19_00:23:25_Dcr.fits 1995_07_19_00:25:21_Dcr.fits 1995_07_19_00:27:16_Dcr.fits 1995_07_19_00:29:19_Dcr.fits 1995_07_19_00:31:16_Dcr.fits 1995_07_19_00:33:14_Dcr.fits To show the R.A.-Dec. tracks do plotRaDec(table, 65) plotRaDec(table, 66) plotRaDec(table, 67) plotRaDec(table, 68) plotRaDec(table, 69) plotRaDec(table, 70) plotRaDec(table, 71) plotRaDec(table, 72) plotRaDec(table, 73) reverseX() After the plot is reversed with reverseX() to make it as seen on the sky, the scanning direction was right to left. To get a plot of R.A. or Dec. as a function of time for one of the scans run plotRA(table, 65) or plotDec(table, 65)
Any number of the scans may be used to plot raw data counts from individual receivers and phases. For example, 1995_07_18_14:36:30_Dcr.fits can used with plotPhase(table, 0, 1|2, 1|2) Plots data counts vs UTC in hrs plotPhaseRA(table, 0, 1|2, 1|2) Plots data counts vs R.A. in hrs To plot a declination scan of data counts vs declination use 1995_07_18_14:38:33_Dcr.fits with plotPhaseDec(table, 1, 1|2, 1|2)
The same two scans in item 3 above may be used to plot calibrated scans. Use 1995_07_18_14:36:30_Dcr.fits with plotTPwCRA(1.6, table, 0, 1|2) Where 1.6 is the cal value in K plotTPwCTime(1.6, table, 0, 1|2) Use 1995_07_18_14:38:33_Dcr.fits with plotTPwCDec(1.6, table, 1, 1|2)
The receiver gain in units of counts per Kelvin may be plotted as a function of UTC. Again, use 1995_07_18_14:36:30_Dcr.fits this time with plotGainTime(1.6, table, 1, 1|2) In this can you can see the effect of using an unsymmetric cal switching cycle which has a tendency to differentiate the intensity-vs-time function, positive when going onto the source and negative when moving off. This is not a real receiver gain variation.
The effect of the data/position timing error that we are tracking down can be seen by overplotting R.A. or Dec. scans taken with opposite scanning directions. For example, use 1995_07_18_14:38:33_Dcr.fits and 1995_07_18_14:40:24_Dcr.fits with plotTPwCDec(1.6, table, 1, 1|2) and plotTPwCDec(1.6, table, 2, 1|2) without clear() between plots
The scan numbers in an aips_table containing more than one scan may be printed with scanNumbers(table)
At the beginning of the July test session we recorded DCR data with the counters connected to the internal test 5 MHz test oscillator to check the internal timing and counter operation of the DCR. A quick comparison between expected and measured counter values may be printed from any of the scans 1995_07_17_17:28:21_Dcr.fits 1995_07_17_17:49:46_Dcr.fits 1995_07_17_17:55:15_Dcr.fits 1995_07_17_17:59:54_Dcr.fits using testDataCheck(table, 0|1|2|3) where the scan numbers, 0|1|2|3, refer to the four data scans, respectively. The output should look something like Rx 1 ph 1 ( 0.24999 s ), expect 1.24995e+06 measured 1.24995e+06 Rx 1 ph 2 ( 0.24999 s ), expect 1.24995e+06 measured 1.24995e+06 Rx 1 ph 3 ( 0.24999 s ), expect 1.24995e+06 measured 1.24995e+06 Rx 1 ph 4 ( 0.24999 s ), expect 1.24995e+06 measured 1.24995e+06 Rx 2 ph 1 ( 0.24999 s ), expect 1.24995e+06 measured 1.24995e+06 Rx 2 ph 2 ( 0.24999 s ), expect 1.24995e+06 measured 1.24995e+06 Rx 2 ph 3 ( 0.24999 s ), expect 1.24995e+06 measured 1.24995e+06 Rx 2 ph 4 ( 0.24999 s ), expect 1.24995e+06 measured 1.24995e+06
We also ran tests on the DCR with its V/F inputs connected to a sine wave oscillator. The following scan shows that the two channels track in gain to about 0.04%. More tests of this sort are planned for the August run when we will us an accurate voltage source to check the absolute gain and linearity of the V/F convertors. 1995_07_17_21:11:18_Dcr.fits To overplot the data from the two channels use plotPhase(table, 11, 1, 1|2) [Bob Garwood adds: I thought I'd take the difference from the two vectors plotted in test.9.a but since I didn't have them available in glish, I relied on the plotting tool to get the values. x0 := getX(0); x1 := getX(1); y0 := getY(0); y1 := getY(1); I verified that x0 is idential to x1 and then displayed the difference ydiff := y0 - y1; plotxy(x0, ydiff, "Rx1 Phase1 - Rx2 Phase1"); ]
We ended up with a puzzling result when trying to use 3C273 to evaluate the tracking accuracy of the 140-ft by putting the source on the beam half-power point. The intensity variation was much greater than could be explained with the position errors as seen on the encoders. We ended up tracking 3C273 at the beam peak, and we found that the source intensity appeared to be varying on time scales of tens of seconds for reasons we still don't understand. The data on and off the source are in 1995_07_19_02:24:27_Dcr.fits 3C273 at beam peak 1995_07_19_02:43:03_Dcr.fits blank sky The plot can be obtained with plotTPwCTime(1.6, table, 3, 1) 3C273 plotTPwCTime(1.6, table, 4, 1) blank sky The overplot of the two scans without clear() between the shows the approximate source antenna temperature and the difference in fluctuation in the two scans. The source and blank sky were at elevations around 20 degrees, which explains the rising antenna temperature with time as the elevation decreased with time. The receiver gain can be plotted on the 3C273 scan with plotGainTime(1.6, tbl4, 3, 2) However, the noise on the gain is too large to rule out the possibility of receiver gain being the cause of the apparent variation (blank sky test aside). A better test is to look for a correlation between source temperature and gain with the following commands: plotTPwCTime(1.6, tbl4, 3, 2) clear() plotGainTime(1.6, tbl4, 3, 2) clear() plotxy(cal_data, cts_per_K, "", style_="points") which shows that there is no obvious correlation between gain an antenna temperature. Note that 'cal_data' and 'cts_per_K' are global variables in the first two plot functions, so they are available to the last 'plotxy()'. A more sensitive test is to look at the cross-correlation between the gain and receiver temperature with the following commands: avg_gain := sum(cts_per_K) / len(cts_per_K) gain := 50.0 * (cts_per_K - avg_gain) / avg_gain avg_data := sum(cal_data) / len(cal_data) data := 50.0 * (cal_data - avg_data) / avg_data cc := crossCor(data, gain) clear() ploty(cc[1:100], "") which shows no significant cross correlation at zero delay when compared with the data autocorrelation function: ccd := crossCor(data, data) ploty(ccd[1:100], "") The small negative peak in the data-gain cross-correlation at a delay of 5 may be due to the differentiation effect mentioned above, which induces a correlation between apparent gain and large slopes in the antenna temperature as a function of time. This conjecture needs to be verified, but it's fascinating what various plots like this turn up.
A typical scan to try fitting a gaussian to is 1995_07_18_01:54:19_Dcr.fits plotTPwCRA(1.6, table, 16, 1) Select the baseline areas to be fitted near the ends of the scan on the plot, then fitTipping() Fit result: Intercept = 29.0987 K, Slope = -0.600722 K/atmos. coeff[1] := 29.0987; coeff[2] := -0.600722 # from fit result y := evalPoly(ra, coeff) y := cal_data - y # remove baseline clear() plotxy(ra, y, "") Select the data range to be fit with the gaussian on the plot. fitOneGaussian(4.76, 13.48, 0.02) # guesses from plot Result: converged = 1 niter = 4 height = 4.88249 center = 13.4806 width = 0.0174697 herr = 0.00867067 cerr = 2.53294e-05 werr = 3.58148e-05 All of our source scans were in strong sources so I don't have any noisey data to try on the fitting routine.
We did two mapping runs which can be run through the contour routine. One was run with 10' spacing (HPBW = 21') and one with 5' spacing. Unfortunately, the 5' spacing map was done during the day and is badly contaminated by the sun. The 10' spacing map of 3C273 is in 1995_07_19_00:17:23_Dcr.fits 1995_07_19_00:19:23_Dcr.fits 1995_07_19_00:21:21_Dcr.fits 1995_07_19_00:23:25_Dcr.fits 1995_07_19_00:25:21_Dcr.fits 1995_07_19_00:27:16_Dcr.fits 1995_07_19_00:29:19_Dcr.fits 1995_07_19_00:31:16_Dcr.fits 1995_07_19_00:33:14_Dcr.fits Run scans := [65:73] mapContour(table, scans) The mapContour() routine is lashed together for these particular data. It works only for west-to-east scanning and north-to-south scan steps. No baselines have been subtracted. Since only three of the nine scans had much flux in them, the inner contours are a bit football shaped. I think I have the coordinates right, but I may be off by a pixel in R.A. It's hard to tell.
Copyright © 1995 Associated Universities Inc., Washington, D.C.