A Multi-dimensional Gaussian functional. More...

#include <GaussianND.h>

Inheritance diagram for casa::GaussianND< T >:

Public Member Functions
	GaussianND ()
	Makes a Gaussian using the indicated height, mean, variance & covariance.
	GaussianND (uInt ndim)
	GaussianND (uInt ndim, const T &height)
	GaussianND (uInt ndim, const T &height, const Vector< T > &mean)
	GaussianND (uInt ndim, const T &height, const Vector< T > &mean, const Vector< T > &variance)
	GaussianND (uInt ndim, const T &height, const Vector< T > &mean, const Matrix< T > &covar)
	GaussianND (const GaussianND &other)
	Copy constructor (deep copy)
GaussianND< T > &	operator= (const GaussianND< T > &other)
	Copy assignment (deep copy)
virtual	~GaussianND ()
	Destructor.
virtual T	eval (typename Function< T >::FunctionArg x) const
	Evaluate the Gaussian at `x`.
virtual Function< T > *	clone () const
	Return a copy of this object from the heap.

Detailed Description

template<class T>
class casa::GaussianND< T >

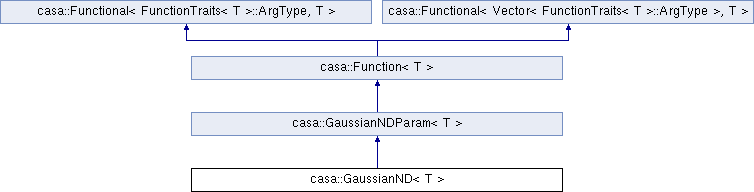
A Multi-dimensional Gaussian functional.

Intended use:

Public interface

 <h3>Review Status</h3><dl><dt>Reviewed By:<dd>UNKNOWN<dt>Date Reviewed:<dd>before2004/08/25<dt>Test programs:<dd>tGaussianND<dt>Demo programs:<dd>dGaussianND</dl>

Prerequisite

Synopsis

A GaussianND is used to calculate Gaussian functions of any dimension. A Gaussian1D class exists which is more appropriate for one dimensional Gaussian functions, and a Gaussian2D class exists for two dimensional functions.

A statistical description of the multi-dimensional Gaussian is used (see Kendall & Stuart "The Advanced Theory of Statistics"). A Gaussian is defined in terms of its height, mean (which is the location of the peak value), variance, (a measure of the width of the Gaussian), and covariance which skews the distribution with respect to the Axes.

In the general description the variance and covariance are specified using a covariance matrix. This is defined as (for a 4 dimensional Gaussian):

     V = |     s1*s1 r12*s1*s2 r13*s1*s3 r14*s1*s4 | 
         | r12*s1*s2     s2*s2 r23*s2*s3 r24*s2*s4 |
         | r13*s1*s3 r23*s2*s3     s3*s3 r34*s3*s4 |
         | r14*s1*s4 r24*s2*s4 r34*s3*s4     s4*s4 |

where s1 (sigma1) is the standard deviation of the Gaussian with respect to the first axis, and r12 (rho12) is the correlation between the the first and second axis. The correlation MUST be between -1 and 1, and this class checks this as well as ensuring that the diagonal is positive.

Warning: It is possible to have symmetric matrices that are of the above described form (ie; symmetric with -1 <= rho(ij) <=1) that do not generate a Gaussian function; This is because the Matrix is NOT positive definite (The limits on rho(ij) are upper limits); This class does check that the covariance Matrix is positive definite and will throw an exception (AipsError) if it is not;

The covariance Matrix can be specified by only its upper or lower triangular regions (ie. with zeros in the other triangle), otherwise it MUST be symmetric.

The Gaussian that is constructed from this covariance Matrix (V), along with mean (u) and height (h) is:

     f(x) = h*exp( -1/2 * (x-u) * V^(-1) * (x-u))

where x, and u are vectors whose length is the dimensionality of the Gaussian and V^(-1) is the inverse of the covariance Matrix defined above. For a two dimensional Gaussian with zero mean this expression reduces to:

    f(x) = h*exp(-1/(2*(1-r12^2))*(x1^2/s1^2 - 2*r12*x1*x2/(s1*s2) + x2^2/s2^2))

The amplitude of the Gaussian can be defined in two ways, either using the peak height (as is done in the constructors, and the setHeight function) or using the setFlux function. The flux in this context is the analytic integral of the Gaussian over all dimensions. Using the setFlux function does not modify the shape of the Gaussian just its height.

All the parameters of the Gaussian except its dimensionality can be modified using the set/get functions.

The parameter interface (see FunctionParam class), is used to provide an interface to the Fitting classes. There are always 4 parameter sets. The parameters are, in order:

height (1 term). No assumptions on what quantity the height represents, and it can be negative
mean (ndim terms).
variance (ndim terms). The variance is always positive, and an exception (AipsError) will be thrown if you try to set a negative value.
covariance (ndim*(ndim-1)/2 terms) The order is (assuming ndim=5) v12,v13,v14,v15,v23,v24,v25,v34,v35,v45. The restrictions described above for the covariance (ie. -1 < r12 < +1) are enforced.

Example

Construct a two dimensional Gaussian with mean=(0,1), variance=(.1,7) and height = 1;

    uInt ndim = 2;
    Float height = 1;
    Vector<Float> mean(ndim); mean(0) = 0, mean(1) = 1;
    Vector<Float> variance(ndim); variance(0) = .1, variance(1) = 7;
    GaussianND<Float> g(ndim, height, mean, variance); 
    Vector<Float> x(ndim); x = 0;
    cout << "g("<< x <<") = " << g(x) <<endl; // g([0,0])=1*exp(-1/2*1/7);
    x(1)++;
    cout << "g("<< x <<") = " <<g(x) <<endl;  // g([0,1])= 1
    cout << "Height: " << g.height() <<endl;    // Height: 1
    cout << "Flux: " << g.flux() << endl;       // Flux: 2*Pi*Sqrt(.1*7)
    cout << "Mean: " << g.mean() << endl;  // Mean: [0, -1]
    cout << "Variance: " << g.variance() <<endl;  // Variance: [.1, 7]
    cout << "Covariance: "<< g.covariance()<<endl;// Covariance: [.1, 0]
                                                          //             [0,  7]
    g.setFlux(1);
    cout << "g("<< x <<") = " <<g(x) <<endl;  //g([0,1])=1/(2*Pi*Sqrt(.7))
    cout << "Height: " << g.height() <<endl;    // Height: 1/(2*Pi*Sqrt(.7))
    cout << "Flux: " << g.flux() << endl;       // Flux: 1
    cout << "Mean: " << g.mean() << endl;  // Mean: [0, -1]
    cout << "Variance: " << g.variance() <<endl;  // Variance: [.1, 7]
    cout << "Covariance: "<< g.covariance()<<endl;// Covariance: [.1, 0]
                                                          //             [0,  7]

Motivation

A Gaussian Functional was needed for modeling the sky with a series of components. It was later realised that it was too general and Gaussian2D was written.

Template Type Argument Requirements (T)

T should have standard numerical operators and exp() function. Current implementation only tested for real types.

To Do

Nothing I know off, apart from possible optimization

Definition at line 178 of file GaussianND.h.

Constructor & Destructor Documentation

template<class T>

casa::GaussianND< T >::GaussianND ( ) [inline]

Makes a Gaussian using the indicated height, mean, variance & covariance.

ndim defaults to 2, mean defaults to 0, height to Pi^(-ndim/2) (the flux is unity) variance defaults to 1.0, covariance defaults to 0.0,

Definition at line 190 of file GaussianND.h.

template<class T>

casa::GaussianND< T >::GaussianND ( uInt ndim ) [inline, explicit]

Definition at line 191 of file GaussianND.h.

template<class T>

casa::GaussianND< T >::GaussianND	(	uInt	ndim,
		const T &	height
	)		`[inline]`

Definition at line 193 of file GaussianND.h.

template<class T>

casa::GaussianND< T >::GaussianND	(	uInt	ndim,
		const T &	height,
		const Vector< T > &	mean
	)		`[inline]`

Definition at line 195 of file GaussianND.h.

template<class T>

casa::GaussianND< T >::GaussianND	(	uInt	ndim,
		const T &	height,
		const Vector< T > &	mean,
		const Vector< T > &	variance
	)		`[inline]`

Definition at line 197 of file GaussianND.h.

template<class T>

casa::GaussianND< T >::GaussianND	(	uInt	ndim,
		const T &	height,
		const Vector< T > &	mean,
		const Matrix< T > &	covar
	)		`[inline]`

Definition at line 200 of file GaussianND.h.

template<class T>

casa::GaussianND< T >::GaussianND ( const GaussianND< T > & other ) [inline]

Copy constructor (deep copy)

Definition at line 207 of file GaussianND.h.

template<class T>

virtual casa::GaussianND< T >::~GaussianND ( ) [inline, virtual]

Destructor.

Definition at line 215 of file GaussianND.h.

Member Function Documentation

template<class T>

virtual Function<T>* casa::GaussianND< T >::clone ( ) const [inline, virtual]

Return a copy of this object from the heap.

The caller is responsible for deleting this pointer.

Implements casa::Function< T >.

Definition at line 227 of file GaussianND.h.

template<class T>

virtual T casa::GaussianND< T >::eval ( typename Function< T >::FunctionArg x ) const [virtual]

Evaluate the Gaussian at x.

template<class T>

GaussianND<T>& casa::GaussianND< T >::operator= ( const GaussianND< T > & other ) [inline]

Copy assignment (deep copy)

Definition at line 211 of file GaussianND.h.

The documentation for this class was generated from the following file:

casacore/scimath/Functionals/GaussianND.h

Public Member Functions

Detailed Description

template<class T> class casa::GaussianND< T >

Intended use:

Prerequisite

Synopsis

Example

Motivation

Template Type Argument Requirements (T)

To Do

Constructor & Destructor Documentation

Member Function Documentation

template<class T>
class casa::GaussianND< T >