Class that computes partial derivatives by automatic differentiation. More...

#include <SparseDiff.h>

Inheritance diagram for casa::SparseDiff< T >:

Public Types
typedef T	value_type
typedef value_type &	reference
typedef const value_type &	const_reference
typedef value_type *	iterator
typedef const value_type *	const_iterator
Public Member Functions
	SparseDiff ()
	Construct a constant with a value of zero.
	SparseDiff (const T &v)
	Construct a constant with a value of v.
	SparseDiff (const T &v, const uInt n)
	A function f(x0,x1,...,xn,...) with a value of v.
	SparseDiff (const T &v, const uInt n, const T &der)
	A function f(x0,x1,...,xn,...) with a value of v.
	SparseDiff (const AutoDiff< T > &other)
	Construct from an AutoDiff.
	SparseDiff (const SparseDiff< T > &other)
	Construct one from another (deep copy)
	~SparseDiff ()
	Destructor.
SparseDiff< T > &	operator= (const T &v)
	Assignment operator.
SparseDiff< T > &	operator= (const pair< uInt, T > &der)
	Assignment operator.
SparseDiff< T > &	operator= (const vector< pair< uInt, T > > &der)
	Assignment operator.
SparseDiff< T > &	operator= (const AutoDiff< T > &other)
	Assign from an Autodiff.
SparseDiff< T > &	operator= (const SparseDiff< T > &other)
	Assign one to another (deep copy)
void	operator*= (const SparseDiff< T > &other)
	Assignment operators.
void	operator/= (const SparseDiff< T > &other)
void	operator+= (const SparseDiff< T > &other)
void	operator-= (const SparseDiff< T > &other)
void	operator*= (const T other)
void	operator/= (const T other)
void	operator+= (const T other)
void	operator-= (const T other)
AutoDiff< T >	toAutoDiff (uInt n) const
	Convert to an AutoDiff of length n
SparseDiffRep< T > *	theRep ()
	Returns the pointer to the structure of value and derivatives.
const SparseDiffRep< T > *	theRep () const
T &	value ()
	Returns the value of the function.
const T &	value () const
vector< pair< uInt, T > > &	derivatives () const
	Returns a vector of the derivatives of a SparseDiff.
void	derivatives (vector< pair< uInt, T > > &res) const
const vector< pair< uInt, T > > &	grad () const
vector< pair< uInt, T > > &	grad ()
pair< uInt, T > &	derivative (uInt which)
	Returns a specific derivative.
const pair< uInt, T > &	derivative (uInt which) const
uInt	nDerivatives () const
	Return total number of derivatives.
Bool	isConstant () const
	Is it a constant, i.e., with zero derivatives?
void	sort ()
	Sort derivative list; cater for doubles and zeroes.
Static Public Member Functions
static Bool	ltSort (pair< uInt, T > &lhs, pair< uInt, T > &rhs)
	Sort criterium.
Private Attributes
SparseDiffRep< T > *	rep_p
	Value representation.

Detailed Description

template<class T>
class casa::SparseDiff< T >

Class that computes partial derivatives by automatic differentiation.

Intended use:

Public interface

Review Status

Reviewed By:: UNKNOWN
Test programs:: tSparseDiff
Demo programs:: dSparseDiff

Prerequisite

AutoDiff class

Etymology

Class that computes partial derivatives for some parameters by automatic differentiation, thus SparseDiff.

Synopsis

Class that computes partial derivatives by automatic differentiation. It does this by storing the value of a function and the values of its first derivatives with respect to some of its independent parameters. When a mathematical operation is applied to a SparseDiff object, the derivative values of the resulting new object are computed according to the chain rules of differentiation. SparseDiff operates like the AutoDiff class, but only determines the derivatives with respect to the actual dependent variables.

Suppose we have a function f(x0,x1,...,xn) and its differential is

      df = (df/dx0)*dx0 + (df/dx1)*dx1 + ... + (df/dxn)*dxn

We can build a class that has the value of the function, f(x0,x1,...,xn), and the values of the derivatives, (df/dx0), (df/dx1), ..., (df/dxn) at (x0,x1,...,xn), as class members.

Now if we have another function, g(x0,x1,...,xn) and its differential is dg = (dg/dx0)*dx0 + (dg/dx1)*dx1 + ... + (dg/dxn)*dxn, since

      d(f+g) = df + dg, 
      d(f*g) = g*df + f*dg, 
      d(f/g) = df/g - fdg/g^2,
      dsin(f) = cos(f)df, 
      ...,

we can calculate

      d(f+g), d(f*g), ...,

based on our information on

      df/dx0, df/dx1, ..., dg/dx0, dg/dx1, ..., dg/dxn.

All we need to do is to define the operators and derivatives of common mathematical functions.

To be able to use the class as an automatic differentiator of a function object, we need a templated function object, i.e. an object with:

a template <class T> T operator()(const T)
or multiple variable input like: template <class T> T operator()(const Vector<T> &)
all dependent variables used in the calculation of the function value should have been typed with T.

A simple example of such a function object could be:

        template <class T> f {
        public:
          T operator()(const T &x, const T &a, const T &b) {
                return a*b*x; }
        };
           // Instantiate the following versions:
        template class f<Double>;
        template class f<SparseDiff<Double> >;

A call with values will produce the function value:

        cout << f(7.0, 2.0, 3.0) << endl;
        // will produce the value at x=7 for a=2; b=3:
        42
        // But a call indicating that we want derivatives to a and b:
        cout << f(SparseDiff<Double>(7.0), SparseDiff<Double>(2.0, 0),
                  SparseDiff<Double>(3.0, 1)) << endl;
        // will produce the value at x=7 for a=2; b=3:
        // and the partial derivatives wrt a and b at x=7:
        (42, [21, 14])
        // The following will calculate the derivate wrt x:
        cout << f(SparseDiff<Double>(7.0, 0), SparseDiff<Double>(2.0),
                  SparseDiff<Double>(3.0)) << endl;
        (42,[6])

Note that in practice constants may be given as Double constants. In actual practice, there are a few rules to obey for the structure of the function object if you want to use the function object and its derivatives in least squares fitting procedures in the Fitting module. The major one is to view the function object having 'fixed' and 'variable' parameters. I.e., rather than viewing the function as depending on parameters a, b, x (f(a,b,x)), the function is considered to be f(x; a,b), where a, b are 'fixed' parameters, and x a variable parameter. Fixed parameters should be contained in a FunctionParam container object; while the variable parameter(s) are given in the function operator(). See Function class for details.

A Gaussian spectral profile would in general have the center frequency, the width and the amplitude as fixed parameters, and the frequency as a variable. Given a spectrum, you would solve for the fixed parameters, given spectrum values. However, in other cases the role of the parameters could be reversed. An example could be a whole stack of observed (in the laboratory) spectra at different temperatures at one frequency. In that case the width would be the variable parameter, and the frequency one of the fixed (and to be solved for)parameters.

Since the calculation of the derivatives is done with simple overloading, the calculation of second (and higher) derivatives is easy. It should be noted that higher deivatives are inefficient in the current incarnation (there is no knowledge e.g. about symmetry in the Jacobian). However, it is a very good way to get the correct answers of the derivatives. In practice actual production code will be better off with specialization of the f<SparseDiff<> > implementation.

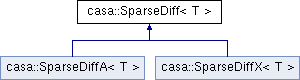
The SparseDiff class is the class the user communicates with. Alias classes ( SparseDiffA and SparseDiffX ) exist to make it possible to have different incarnations of a templated method (e.g. a generic one and a specialized one). See the dSparseDiff demo for an example of its use.

All operators and functions are declared in (see (file=SparseDiffMath.h)) SparseDiffMath . The output operator in (see (file=SparseDiffIO.h))SparseDiffIO . The actual structure of the data block used by SparseDiff is described in SparseDiffRep .

A SparseDiff can be constructed from an AutoDiff. toAutoDiff(n) can convert it to an AutoDiff.

Example

      // First a simple example.
      // We have a function of the form f(x,y,z); and want to know the
      // value of the function for x=10; y=20; z=30; and for
      // the derivatives at those points.
      // Specify the values; and indicate the parameter dependence:
        SparseDiff<Double> x(10.0, 0); 
        SparseDiff<Double> y(20.0, 1); 
        SparseDiff<Double> z(30.0, 2);
      // The result will be:
        SparseDiff<Double> result = x*y + sin(z);
        cout << result.value() << endl;
      // 199.012
        cout << result.derivatives() << endl;
      // [20, 10, 0.154251]
      // Note: sin(30) = -0.988; cos(30) =  0.154251;

See for an extensive example the demo program dSparseDiff. It is based on the example given above, and shows also the use of second derivatives (which is just using SparseDiff<SparseDiff<Double> > as template argument).

        // The function, with fixed parameters a,b:
        template <class T> class f {
        public:
          T operator()(const T& x) { return a_p*a_p*a_p*b_p*b_p*x; }
          void set(const T& a, const T& b) { a_p = a; b_p = b; }
        private:
          T a_p;
          T b_p;
        };
        // Call it with different template arguments:
          Double a0(2), b0(3), x0(7);
          f<Double> f0; f0.set(a0, b0);
          cout << "Value:     " << f0(x0) << endl;
        
          SparseDiff<Double> a1(2,0), b1(3,1), x1(7);
          f<SparseDiff<Double> > f1; f1.set(a1, b1);
          cout << "Diff a,b:   " << f1(x1) << endl;
        
          SparseDiff<Double> a2(2), b2(3), x2(7,0);
          f<SparseDiff<Double> > f2; f2.set(a2, b2);
          cout << "Diff x:     " << f2(x2) << endl;
        
          SparseDiff<SparseDiff<Double> > a3(SparseDiff<Double>(2,0),0),
            b3(SparseDiff<Double>(3,1),1), x3(SparseDiff<Double>(7));
          f<SparseDiff<SparseDiff<Double> > > f3; f3.set(a3, b3);
          cout << "Diff2 a,b:  " << f3(x3) << endl;
        
          SparseDiff<SparseDiff<Double> > a4(SparseDiff<Double>(2)),
            b4(SparseDiff<Double>(3)),
            x4(SparseDiff<Double>(7,0),0);
          f<SparseDiff<SparseDiff<Double> > > f4; f4.set(a4, b4);
          cout << "Diff2 x:    " << f4(x4) << endl;
     
         // Result will be:
         // Value:     504
         // Diff a,b:  (504, [756, 336])
         // Diff x:    (504, [72])
         // Diff2 a,b: ((504, [756, 336]), [(756, [756, 504]), (336, [504, 112])])
         // Diff2 x:   ((504, [72]), [(72, [0])])
     
         // It needed the template instantiations definitions:
        template class f<Double>;
        template class f<SparseDiff<Double> >;
        template class f<SparseDiff<SparseDiff<Double> > >;

Motivation

The creation of the class was motivated by least-squares non-linear fits in cases where each individual condition equation depends only on a fraction of the fixed parameters (e.g. self-calibration where only pairs of antennas are present per equation), and hence only a few partial derivatives of a fitted function are needed. It would be tedious to create functionals for all partial derivatives of a function.

Template Type Argument Requirements (T)

any class that has the standard mathematical and comparison operators and functions defined.

To Do

Nothing I know of.

Definition at line 279 of file SparseDiff.h.

Member Typedef Documentation

template<class T>

typedef const value_type* casa::SparseDiff< T >::const_iterator

Definition at line 286 of file SparseDiff.h.

template<class T>

typedef const value_type& casa::SparseDiff< T >::const_reference

Definition at line 284 of file SparseDiff.h.

template<class T>

typedef value_type* casa::SparseDiff< T >::iterator

Definition at line 285 of file SparseDiff.h.

template<class T>

typedef value_type& casa::SparseDiff< T >::reference

Definition at line 283 of file SparseDiff.h.

template<class T>

typedef T casa::SparseDiff< T >::value_type

Definition at line 282 of file SparseDiff.h.

Constructor & Destructor Documentation

template<class T>

casa::SparseDiff< T >::SparseDiff ( )

Construct a constant with a value of zero.

Zero derivatives.

template<class T>

casa::SparseDiff< T >::SparseDiff ( const T & v )

Construct a constant with a value of v.

Zero derivatives.

template<class T>

casa::SparseDiff< T >::SparseDiff	(	const T &	v,
		const uInt	n
	)

A function f(x0,x1,...,xn,...) with a value of v.

The nth derivative is one, and all other derivatives are zero.

template<class T>

casa::SparseDiff< T >::SparseDiff	(	const T &	v,
		const uInt	n,
		const T &	der
	)

A function f(x0,x1,...,xn,...) with a value of v.

The nth derivative is der, and all other derivatives are zero.

template<class T>

casa::SparseDiff< T >::SparseDiff ( const AutoDiff< T > & other )

Construct from an AutoDiff.

template<class T>

casa::SparseDiff< T >::SparseDiff ( const SparseDiff< T > & other )

Construct one from another (deep copy)

template<class T>

casa::SparseDiff< T >::~SparseDiff ( )

Destructor.

Member Function Documentation

template<class T>

pair<uInt, T>& casa::SparseDiff< T >::derivative ( uInt which ) [inline]

Returns a specific derivative.

No check for a valid which.

Definition at line 366 of file SparseDiff.h.

References casa::SparseDiff< T >::rep_p.

template<class T>

const pair<uInt, T>& casa::SparseDiff< T >::derivative ( uInt which ) const [inline]

Definition at line 367 of file SparseDiff.h.

References casa::SparseDiff< T >::rep_p.

template<class T>

vector<pair<uInt, T> >& casa::SparseDiff< T >::derivatives ( ) const

Returns a vector of the derivatives of a SparseDiff.

template<class T>

void casa::SparseDiff< T >::derivatives ( vector< pair< uInt, T > > & res ) const

template<class T>

const vector<pair<uInt, T> >& casa::SparseDiff< T >::grad ( ) const [inline]

Definition at line 360 of file SparseDiff.h.

References casa::SparseDiff< T >::rep_p.

template<class T>

vector<pair<uInt, T> >& casa::SparseDiff< T >::grad ( ) [inline]

Definition at line 361 of file SparseDiff.h.

References casa::SparseDiff< T >::rep_p.

template<class T>

Bool casa::SparseDiff< T >::isConstant ( ) const [inline]

Is it a constant, i.e., with zero derivatives?

Definition at line 375 of file SparseDiff.h.

References casa::SparseDiff< T >::rep_p.

template<class T>

static Bool casa::SparseDiff< T >::ltSort	(	pair< uInt, T > &	lhs,
		pair< uInt, T > &	rhs
	)		`[static]`

Sort criterium.

template<class T>

uInt casa::SparseDiff< T >::nDerivatives ( ) const [inline]

Return total number of derivatives.

Definition at line 372 of file SparseDiff.h.

References casa::SparseDiff< T >::rep_p.

template<class T>

void casa::SparseDiff< T >::operator*= ( const SparseDiff< T > & other )

Assignment operators.

template<class T>

void casa::SparseDiff< T >::operator*= ( const T other ) [inline]

Definition at line 333 of file SparseDiff.h.

References casa::SparseDiff< T >::rep_p, and casa::SparseDiff< T >::value().

template<class T>

void casa::SparseDiff< T >::operator+= ( const SparseDiff< T > & other )

template<class T>

void casa::SparseDiff< T >::operator+= ( const T other ) [inline]

Definition at line 337 of file SparseDiff.h.

References casa::SparseDiff< T >::value().

template<class T>

void casa::SparseDiff< T >::operator-= ( const SparseDiff< T > & other )

template<class T>

void casa::SparseDiff< T >::operator-= ( const T other ) [inline]

Definition at line 338 of file SparseDiff.h.

References casa::SparseDiff< T >::value().

template<class T>

void casa::SparseDiff< T >::operator/= ( const SparseDiff< T > & other )

template<class T>

void casa::SparseDiff< T >::operator/= ( const T other ) [inline]

Definition at line 335 of file SparseDiff.h.

References casa::SparseDiff< T >::rep_p, and casa::SparseDiff< T >::value().

template<class T>

SparseDiff<T>& casa::SparseDiff< T >::operator= ( const T & v )

Assignment operator.

Assign a constant to variable.

Reimplemented in casa::SparseDiffA< T >, and casa::SparseDiffX< T >.

template<class T>

SparseDiff<T>& casa::SparseDiff< T >::operator= ( const pair< uInt, T > & der )

Assignment operator.

Add a gradient to variable.

Reimplemented in casa::SparseDiffA< T >, and casa::SparseDiffX< T >.

template<class T>

SparseDiff<T>& casa::SparseDiff< T >::operator= ( const vector< pair< uInt, T > > & der )

Assignment operator.

Assign gradients to variable.

Reimplemented in casa::SparseDiffA< T >, and casa::SparseDiffX< T >.

template<class T>

SparseDiff<T>& casa::SparseDiff< T >::operator= ( const AutoDiff< T > & other )

Assign from an Autodiff.

template<class T>

SparseDiff<T>& casa::SparseDiff< T >::operator= ( const SparseDiff< T > & other )

Assign one to another (deep copy)

Reimplemented in casa::SparseDiffX< T >, and casa::SparseDiffA< T >.

template<class T>

void casa::SparseDiff< T >::sort ( )

Sort derivative list; cater for doubles and zeroes.

template<class T>

SparseDiffRep<T>* casa::SparseDiff< T >::theRep ( ) [inline]

Returns the pointer to the structure of value and derivatives.

Definition at line 346 of file SparseDiff.h.

References casa::SparseDiff< T >::rep_p.

template<class T>

const SparseDiffRep<T>* casa::SparseDiff< T >::theRep ( ) const [inline]

Definition at line 347 of file SparseDiff.h.

References casa::SparseDiff< T >::rep_p.

template<class T>

AutoDiff<T> casa::SparseDiff< T >::toAutoDiff ( uInt n ) const

Convert to an AutoDiff of length n

template<class T>

T& casa::SparseDiff< T >::value ( ) [inline]

Returns the value of the function.

Definition at line 352 of file SparseDiff.h.

References casa::SparseDiff< T >::rep_p.

Referenced by casa::SparseDiff< T >::operator*=(), casa::SparseDiff< T >::operator+=(), casa::SparseDiff< T >::operator-=(), and casa::SparseDiff< T >::operator/=().

template<class T>

const T& casa::SparseDiff< T >::value ( ) const [inline]

Definition at line 353 of file SparseDiff.h.

References casa::SparseDiff< T >::rep_p.

Member Data Documentation

template<class T>

SparseDiffRep<T>* casa::SparseDiff< T >::rep_p [private]

Value representation.

Definition at line 386 of file SparseDiff.h.

Referenced by casa::SparseDiff< T >::derivative(), casa::SparseDiff< T >::grad(), casa::SparseDiff< T >::isConstant(), casa::SparseDiff< T >::nDerivatives(), casa::SparseDiff< T >::operator*=(), casa::SparseDiff< T >::operator/=(), casa::SparseDiff< T >::theRep(), and casa::SparseDiff< T >::value().

The documentation for this class was generated from the following file:

casacore/scimath/Mathematics/SparseDiff.h

Public Types

Public Member Functions

Static Public Member Functions

Private Attributes

Detailed Description

template<class T> class casa::SparseDiff< T >

Intended use:

Review Status

Prerequisite

Etymology

Synopsis

Example

Motivation

Template Type Argument Requirements (T)

To Do

Member Typedef Documentation

Constructor & Destructor Documentation

Member Function Documentation

Member Data Documentation

template<class T>
class casa::SparseDiff< T >