casa::Gaussian3D< T > Class Template Reference

A three dimensional Gaussian class. More...

#include <Gaussian3D.h>

Inheritance diagram for casa::Gaussian3D< T >:

List of all members.

Public Member Functions
	Gaussian3D ()
	A functional for a rotated, 3D Gaussian.
	Gaussian3D (T height, const Vector< T > &center, const Vector< T > &width, T theta, T phi)
	Gaussian3D (T &height, T &xCenter, T &yCenter, T &zCenter, T &xWidth, T &yWidth, T &zWidth, T &theta, T &phi)
	Gaussian3D (const Gaussian3D< T > &other)
	Copy constructor.
template<class W >
	Gaussian3D (const Gaussian3D< W > &other)
virtual	~Gaussian3D ()
	Destructor.
Gaussian3D< T > &	operator= (const Gaussian3D< T > &other)
	Assignment operator.
virtual T	eval (typename Function< T >::FunctionArg x) const
	Evaluate the Gaussian at x.
virtual Function< T > *	clone () const
	Return a copy of this object from the heap.
virtual Function< typename FunctionTraits< T >::DiffType > *	cloneAD () const
virtual Function< typename FunctionTraits< T >::BaseType > *	cloneNonAD () const
Private Member Functions
T	sq (T v) const

---

Detailed Description

template<class T>
class casa::Gaussian3D< T >

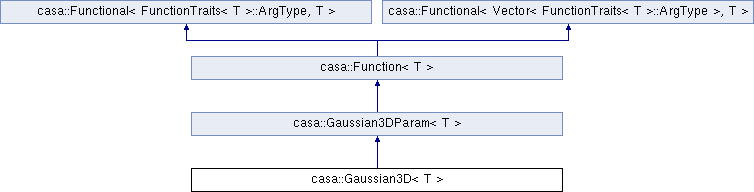
A three dimensional Gaussian class.

Intended use:

Public interface

Review Status

Test programs:

tGaussian3D

Prerequisite

• Gaussian3DParam
• Function

Etymology

A Gaussian3D functional is designed exclusively for calculating a Gaussian (or Normal) distribution in three dimensions. Other classes exist for calculating these functions in one ( Gaussian1D ), two ( Gaussian2D ), and N ( GaussianND ) dimensions.

Synopsis

A Gaussian3D is described by a height, center, and width, and position angles. Its fundamental operation is evaluating itself at some (x,y,z) coordinate. Its parameters (height, center and width, position angles) may be changed at run time.

The width of the Gaussian is now specified in terms of the full width at half maximum (FWHM), like the 2D and 1D Gaussian functional classes.

The three axis values refer to the x, y, and z axes, and unlike with the 2D Gaussian any of the three axes may be the longest; instead, the position angles are restricted. The first position angle, theta, is the longitudinal angle, referring to the rotation (counterclockwise) around the z-axis. The second, phi, is the latidudinal angle, referring to the rotation around the theta-rotated y axis. The domain of both angles is -pi/4 < A < pi/4, although the angles are not constrained when fitting and can be set outside the domain by setting the parameters directly using Functional operator[]. (Note that the use of theta and phi corresponds to the mathematics convention for these angles, not the physics convention.)

The parameter interface (see Gaussian3DParam class), is used to provide an interface to the Fitting classes.

There are 9 parameters that are used to describe the Gaussian:

1. The height of the Gaussian. This is identical to the value returned using the height member function.
2. The center of the Gaussian in the x direction. This is identical to the value returned using the xCenter member function.
3. The center of the Gaussian in the y direction. This is identical to the value returned using the yCenter member function.
4. The center of the Gaussian in the z direction. This is identical to the value returned using the zCenter member function.
5. The width of the Gaussian along the x-axis.
6. The width of the Gaussian along the y-axis.
7. The width of the Gaussian along the z-axis.
8. The longitudinal position angle, theta (in radians)
9. The latitudinal position angle, phi (also in radians).

An enumeration for the parameter index is provided, enabling the setting and reading of parameters with the [] operator. The mask() methods can be used to check and set the parameter masks.

Example

    Gaussian3D<Double> g(9.0, 0.0, 0.0, 0.0, 1.0, 1.0, 1.0, 0.0, 0.0);
    Vector<Double> x(3);
    x(0) = 1.0; x(1) = 0.5; x(2) = 0.0
    cout << "g(" << x(0) << "," << x(1) << "," << x(2) << ")=" << g(x) << endl;

Motivation

The GaussianND class does not contain explicit derivatives and was insufficient for fitting 3D Gaussians to data.

Template Type Argument Requirements (T)

• T should have standard numerical operators and exp() function. Current implementation only tested for real types.
• To obtain derivatives, the derivatives should be defined.

Thrown Exceptions

• Assertion in debug mode if attempt is made to set a negative width
• AipsError if incorrect parameter number specified.
• Assertion in debug mode if operator(Vector<>) with empty Vector

To Do

• Optimize derivative calculations for faster fitting?

Definition at line 145 of file Gaussian3D.h.

---

Constructor & Destructor Documentation

template<class T>

casa::Gaussian3D< T >::Gaussian3D

(

)

A functional for a rotated, 3D Gaussian.

Similar to Gaussian2D, but the xWidth, yWidth, and zWidth parameters are not adjusted for FWHM; they are identical to the parameters used in the function.

Constructs the three-dimensional Gaussians. Defaults: height = 1, center = {0,0,0}, width = {1,1,1}, theta = phi = 0. The center and width vectors must have three elements.

template<class T>

casa::Gaussian3D< T >::Gaussian3D	(	T	height,
		const Vector< T > &	center,
		const Vector< T > &	width,
		T	theta,
		T	phi
	)

template<class T>

casa::Gaussian3D< T >::Gaussian3D	(	T &	height,
		T &	xCenter,
		T &	yCenter,
		T &	zCenter,
		T &	xWidth,
		T &	yWidth,
		T &	zWidth,
		T &	theta,
		T &	phi
	)

template<class T>

casa::Gaussian3D< T >::Gaussian3D

(

const Gaussian3D< T > &

other

)

Copy constructor.

template<class T>

template<class W >

casa::Gaussian3D< T >::Gaussian3D

(

const Gaussian3D< W > &

other

)

[inline]

Definition at line 167 of file Gaussian3D.h.

template<class T>

virtual casa::Gaussian3D< T >::~Gaussian3D

(

)

[virtual]

Destructor.

---

Member Function Documentation

template<class T>

virtual Function<T>* casa::Gaussian3D< T >::clone

(

)

const [virtual]

Return a copy of this object from the heap.

The caller is responsible for deleting this pointer.

Implements casa::Function< T >.

template<class T>

virtual Function<typename FunctionTraits<T>::DiffType>* casa::Gaussian3D< T >::cloneAD

(

)

const [inline, virtual]

Reimplemented from casa::Function< T >.

Definition at line 183 of file Gaussian3D.h.

template<class T>

virtual Function<typename FunctionTraits<T>::BaseType>* casa::Gaussian3D< T >::cloneNonAD

(

)

const [inline, virtual]

Reimplemented from casa::Function< T >.

Definition at line 185 of file Gaussian3D.h.

template<class T>

virtual T casa::Gaussian3D< T >::eval

(

typename Function< T >::FunctionArg

x

)

const [virtual]

Evaluate the Gaussian at x.

template<class T>

Gaussian3D<T>& casa::Gaussian3D< T >::operator=

(

const Gaussian3D< T > &

other

)

Assignment operator.

template<class T>

T casa::Gaussian3D< T >::sq

(

T

v

)

const [private]

AutoDiff does not have a square() function, so one is provided here.

---

The documentation for this class was generated from the following file:

• casacore/scimath/Functionals/Gaussian3D.h