Generic base class for least-squares fit. More...

#include <GenericL2Fit.h>

Inheritance diagram for casa::GenericL2Fit< T >:

Public Member Functions
	GenericL2Fit ()
	Create a fitter: the normal way to generate a fitter object.
	GenericL2Fit (const GenericL2Fit &other)
	Copy constructor (deep copy)
GenericL2Fit &	operator= (const GenericL2Fit &other)
	Assignment (deep copy)
virtual	~GenericL2Fit ()
	Destructor.
template<class U >
void	setFunction (const Function< U, U > &function)
	Sets the function to be fitted.
template<class U >
Bool	setConstraint (const uInt n, const Function< U, U > &function, const Vector< typename FunctionTraits< T >::BaseType > &x, const typename FunctionTraits< T >::BaseType y=typename FunctionTraits< T >::BaseType(0))
	Set the possible constraint functions.
Bool	setConstraint (const uInt n, const Vector< typename FunctionTraits< T >::BaseType > &x, const typename FunctionTraits< T >::BaseType y=typename FunctionTraits< T >::BaseType(0))
Bool	setConstraint (const uInt n, const typename FunctionTraits< T >::BaseType y=typename FunctionTraits< T >::BaseType(0))
Bool	addConstraint (const Function< typename FunctionTraits< T >::DiffType, typename FunctionTraits< T >::DiffType > &function, const Vector< typename FunctionTraits< T >::BaseType > &x, const typename FunctionTraits< T >::BaseType y=typename FunctionTraits< T >::BaseType(0))
Bool	addConstraint (const Vector< typename FunctionTraits< T >::BaseType > &x, const typename FunctionTraits< T >::BaseType y=typename FunctionTraits< T >::BaseType(0))
Bool	addConstraint (const typename FunctionTraits< T >::BaseType y=typename FunctionTraits< T >::BaseType(0))
void	setCollinearity (const Double cln)
	Set the collinearity factor as the square of the sine of the minimum angle allowed between input vectors (default zero for non-SVD, 1e-8 for SVD)
void	asWeight (const Bool aswgt)
	Set sigma values to be interpreted as weight (i.e.
void	asSVD (const Bool svd)
	Set the use of SVD or not (default).
Function< typename FunctionTraits< T >::DiffType, typename FunctionTraits< T > ::DiffType > *	fittedFunction ()
	Return a pointer to the function being fitted.
const Function< typename FunctionTraits< T >::DiffType, typename FunctionTraits< T > ::DiffType > *	fittedFunction () const
uInt	fittedNumber () const
	Return the number of fitted parameters.
uInt	NConstraints ()
	Return the number of constraints, and pointers to constraint functions.
Function< typename FunctionTraits< T >::DiffType, typename FunctionTraits< T > ::DiffType > *	getConstraint (const uInt n)
Vector< typename LSQTraits < typename FunctionTraits< T > ::BaseType >::base >	getSVDConstraint (uInt n)
	Return the nth constraint equation derived from SVD Note that the number present will be given by `getDeficiency()`
void	setParameterValues (const Vector< typename FunctionTraits< T >::BaseType > &parms)
	Set the parameter values.
void	setMaskedParameterValues (const Vector< typename FunctionTraits< T >::BaseType > &parms)
Vector< typename FunctionTraits< T >::BaseType >	fit (const Vector< typename FunctionTraits< T >::BaseType > &x, const Vector< typename FunctionTraits< T >::BaseType > &y, const Vector< typename FunctionTraits< T >::BaseType > &sigma, const Vector< Bool > *const mask=0)
	Fit the function to the data.
Vector< typename FunctionTraits< T >::BaseType >	fit (const Matrix< typename FunctionTraits< T >::BaseType > &x, const Vector< typename FunctionTraits< T >::BaseType > &y, const Vector< typename FunctionTraits< T >::BaseType > &sigma, const Vector< Bool > *const mask=0)
Vector< typename FunctionTraits< T >::BaseType >	fit (const Vector< typename FunctionTraits< T >::BaseType > &x, const Vector< typename FunctionTraits< T >::BaseType > &y, const Vector< Bool > *const mask=0)
Vector< typename FunctionTraits< T >::BaseType >	fit (const Matrix< typename FunctionTraits< T >::BaseType > &x, const Vector< typename FunctionTraits< T >::BaseType > &y, const Vector< Bool > *const mask=0)
Vector< typename FunctionTraits< T >::BaseType >	fit (const Vector< Bool > *const mask=0)
Bool	fit (Vector< typename FunctionTraits< T >::BaseType > &sol, const Vector< typename FunctionTraits< T >::BaseType > &x, const Vector< typename FunctionTraits< T >::BaseType > &y, const Vector< typename FunctionTraits< T >::BaseType > &sigma, const Vector< Bool > *const mask=0)
Bool	fit (Vector< typename FunctionTraits< T >::BaseType > &sol, const Matrix< typename FunctionTraits< T >::BaseType > &x, const Vector< typename FunctionTraits< T >::BaseType > &y, const Vector< typename FunctionTraits< T >::BaseType > &sigma, const Vector< Bool > *const mask=0)
Bool	fit (Vector< typename FunctionTraits< T >::BaseType > &sol, const Vector< typename FunctionTraits< T >::BaseType > &x, const Vector< typename FunctionTraits< T >::BaseType > &y, const typename FunctionTraits< T >::BaseType &sigma, const Vector< Bool > *const mask=0)
Bool	fit (Vector< typename FunctionTraits< T >::BaseType > &sol, const Matrix< typename FunctionTraits< T >::BaseType > &x, const Vector< typename FunctionTraits< T >::BaseType > &y, const typename FunctionTraits< T >::BaseType &sigma, const Vector< Bool > *const mask=0)
Bool	fit (Vector< typename FunctionTraits< T >::BaseType > &sol, const Vector< Bool > *const mask=0)
Double	chiSquare () const
	Obtain the chi squared.
const Vector< typename FunctionTraits< T >::BaseType > &	errors () const
	Get the errors on the solved values.
Bool	errors (Vector< typename FunctionTraits< T >::BaseType > &err) const
Matrix< Double >	compuCovariance ()
	Get covariance matrix.
void	compuCovariance (Matrix< Double > &cov)
void	buildNormalMatrix (const Vector< typename FunctionTraits< T >::BaseType > &x, const Vector< typename FunctionTraits< T >::BaseType > &y, const Vector< typename FunctionTraits< T >::BaseType > &sigma, const Vector< Bool > *const mask=0)
	Generate the normal equations by one or more calls to the buildNormalMatrix(), before calling a fit() without arguments.
void	buildNormalMatrix (const Matrix< typename FunctionTraits< T >::BaseType > &x, const Vector< typename FunctionTraits< T >::BaseType > &y, const Vector< typename FunctionTraits< T >::BaseType > &sigma, const Vector< Bool > *const mask=0)
void	buildNormalMatrix (const Vector< typename FunctionTraits< T >::BaseType > &x, const Vector< typename FunctionTraits< T >::BaseType > &y, const Vector< Bool > *const mask=0)
void	buildNormalMatrix (const Matrix< typename FunctionTraits< T >::BaseType > &x, const Vector< typename FunctionTraits< T >::BaseType > &y, const Vector< Bool > *const mask=0)
Bool	residual (Vector< typename FunctionTraits< T >::BaseType > &y, const Array< typename FunctionTraits< T >::BaseType > &x, const Vector< typename FunctionTraits< T >::BaseType > &sol, const Bool model=False)
	Return the residual after a fit in y.
Bool	residual (Vector< typename FunctionTraits< T >::BaseType > &y, const Array< typename FunctionTraits< T >::BaseType > &x, const Bool model=False)
uInt	getRank () const
	Get the rank of the solution (or zero of no fit() done yet).
Public Attributes
const Double	COLLINEARITY
	Default collinearity test for SVD.
Protected Member Functions
virtual Bool	fitIt (Vector< typename FunctionTraits< T >::BaseType > &sol, const Array< typename FunctionTraits< T >::BaseType > &x, const Vector< typename FunctionTraits< T >::BaseType > &y, const Vector< typename FunctionTraits< T >::BaseType > const sigma, const Vector< Bool > const mask=0)=0
	Generalised fitter.
void	buildMatrix (const Array< typename FunctionTraits< T >::BaseType > &x, const Vector< typename FunctionTraits< T >::BaseType > &y, const Vector< typename FunctionTraits< T >::BaseType > const sigma, const Vector< Bool > const mask=0)
	Build the normal matrix.
void	buildConstraint ()
	Build the constraint equations.
void	fillSVDConstraints ()
	Get the SVD constraints.
Bool	buildResidual (Vector< typename FunctionTraits< T >::BaseType > &y, const Array< typename FunctionTraits< T >::BaseType > &x, const Vector< typename FunctionTraits< T >::BaseType > *const sol, const Bool model=False)
	Calculate residuals.
FunctionTraits< T >::BaseType	getVal_p (const Array< typename FunctionTraits< T >::BaseType > &x, uInt j, uInt i) const
	Function to get evaluated functional value.
void	initfit_p (uInt parcnt)
	Initialise the fitter with number of solvable parameters.
uInt	testInput_p (const Array< typename FunctionTraits< T >::BaseType > &x, const Vector< typename FunctionTraits< T >::BaseType > &y, const Vector< typename FunctionTraits< T >::BaseType > *const sigma)
	Return number of condition equations and check sizes x, y, sigma.
void	resetFunction ()
	Reset all the input.
Protected Attributes
uInt	aCount_ai
	Adjustable.
Bool	svd_p
	SVD indicator.
Function< typename FunctionTraits< T >::DiffType, typename FunctionTraits< T > ::DiffType > *	ptr_derive_p
	Function to use in evaluating condition equation.
PtrBlock< Function< typename FunctionTraits< T >::DiffType, typename FunctionTraits< T > ::DiffType > * >	constrFun_p
	List of functions describing the possible constraint equations e.g.
PtrBlock< Vector< typename FunctionTraits< T >::BaseType > * >	constrArg_p
	List of vectors describing the constraint equations' arguments.
PtrBlock< typename FunctionTraits< T >::BaseType * >	constrVal_p
	List of values describing the constraint equations' value.
uInt	pCount_p
	Number of available parameters.
uInt	ndim_p
	Number of dimensions of input data.
Bool	needInit_p
	No normal equations yet.
Bool	solved_p
	Have solution.
Bool	errors_p
	Have errors.
Bool	ferrors_p
Bool	asweight_p
	Interpret as weights rather than as sigma the given values.
uInt	nr_p
	The rank of the solution.
Vector< typename FunctionTraits< T >::BaseType >	condEq_p
	Condition equation parameters (for number of adjustable parameters)
Vector< typename FunctionTraits< T >::BaseType >	fullEq_p
	Equation for all available parameters.
Vector< typename FunctionTraits< T >::ArgType >	arg_p
	Contiguous argument areas.
Vector< typename FunctionTraits< T >::ArgType >	carg_p
Vector< typename FunctionTraits< T >::BaseType >	sol_p
	Local solution area.
Vector< typename FunctionTraits< T >::BaseType >	fsol_p
Vector< typename FunctionTraits< T >::BaseType >	err_p
	Local error area.
Vector< typename FunctionTraits< T >::BaseType >	ferr_p
FunctionTraits< T >::DiffType	valder_p
	Local value and derivatives.
Vector< Vector< typename LSQTraits< typename FunctionTraits< T >::BaseType > ::base > >	consvd_p
	Local SVD constraints.
Private Member Functions
void	setFunctionEx ()
	Set function properties.
Bool	setConstraintEx (const uInt n, const Vector< typename FunctionTraits< T >::BaseType > &x, const typename FunctionTraits< T >::BaseType y)
	Set Constraint properties.

Detailed Description

template<class T>
class casa::GenericL2Fit< T >

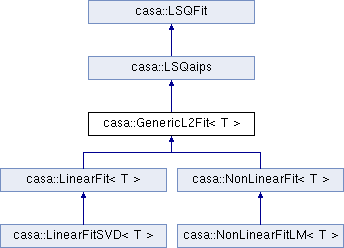
Generic base class for least-squares fit.

Review Status

Reviewed By:: wbrouw
Date Reviewed:: 2004/06/14
Test programs:: tLinearFitSVD

Prerequisite

Function
Fitting

Etymology

A set of data point is fit with some functional equation. The class acts as a generic base class for L2 type fits.

Synopsis

NOTE: Constraints added. Documentation out of date at moment, check the tLinearFitSVD and tNonLinearFitLM programs for examples.

The class acts as a base class for L2-type (least-squares) fitting. Actual classes (se e.g. LinearFit and NonLinearFit .

The following is a brief summary of the linear least-squares fit problem. See module header, Fitting , for a more complete description.

Given a set of N data points (measurements), (x(i), y(i)) i = 0,...,N-1, along with a set of standard deviations, sigma(i), for the data points, and M specified functions, f(j)(x) j = 0,...,M-1, we form a linear combination of the functions:

    z(i) = a(0)f(0)(x(i)) + a(1)f(1)(x(i)) + ... + a(M-1)f(M-1)(x(i)),

where a(j) j = 0,...,M-1 are a set of parameters to be determined. The linear least-squares fit tries to minimize

    chi-square = [(y(0)-z(0))/sigma(0)]^2 + [(y(1)-z(1))/sigma(1)]^2 + ..\.
                 + [(y(N-1)-z(N-1))/sigma(N-1)]^2.

by adjusting {a(j)} in the equation.

For complex numbers, [(y(i)-z(i))/sigma(i)]^2 in chi-square is replaced by [(y(i)-z(i))/sigma(i)]*conjugate([(y(i)-z(i))/sigma(i)])

For multidimensional functions, x(i) is a vector, and

    f(j)(x(i)) = f(j)(x(i,0), x(i,1), x(i,2), ...)

Normally, it is necessary that N > M for the solutions to be valid, since there must be more data points than model parameters to be solved.

If the measurement errors (standard deviation sigma) are not known at all, they can all be set to one initially. In this case, we assume all measurements have the same standard deviation, after minimizing chi-square, we recompute

    sigma^2 = {(y(0)-z(0))^2 + (y(1)-z(1))^2 + ..\.
              + (y(N-1)-z(N-1))^2}/(N-M) = chi-square/(N-M).

A statistic weight can also be assigned to each measurement if the standard deviation is not available. sigma can be calculated from

    sigma = 1/ sqrt(weight)

Alternatively a 'weight' switch can be set with asWeight(). For best arithmetic performance, weight should be normalized to a maximum value of one. Having a large weight value can sometimes lead to overflow problems.

The function to be fitted to the data can be given as an instance of the Function class. One can also form a sum of functions using the CompoundFunction .

For small datasets the usage of the calls is:

Create a functional description of the parameters
Create a fitter: GenericL2Fit<T> fitter();
Set the functional representation: fitter.setFunction()
Do the fit to the data: fitter.fit(x, data, sigma) (or do a number of calls to buildNormalMatrix(x, data, sigma) and finish of with fitter.fit() or fitter.sol())
if needed the covariance; residuals; chiSquared, parameter errors can all be obtained

Note that the fitter is reusable. An example is given in the following.

The solution of a fit always produces the total number of parameters given to the fitter. I.e. including any parameters that were fixed. In the latter case the solution returned will be the fixed value.

Template Type Argument Requirements (T)

The following data types can be used to instantiate the GenericL2Fit templated class: Known classes for FunctionTraits. I.e simple numerical like Float, Double, Complex, DComplex; and the AutoDiff<> versions.

If there are a large number of unknowns or a large number of data points machine memory limits (or timing reasons) may not allow a complete in-core fitting to be performed. In this case one can incrementally build the normal equation (see buildNormalMatrix()).

The normal operation of the class tests for real inversion problems only. If tests are needed for almost collinear columns in the solution matrix, the collinearity can be set as the square of the sine of the minimum angle allowed.

Singular Value Decomposition is supported by the asSVD() (which will also set the default collinearity to 1e-8).

Other information (see a.o. LSQFit ) can be set and obtained as well.

Motivation

The creation of this class was driven by the need to write code to perform baseline fitting or continuum subtraction.

Example

In the following a polynomial is fitted through the first 20 prime numbers. The data is given in the x vector (1 to 20) and in the primesTable (2, 3, ..., 71) (see tLinearFitSVD test program). In the following all four methods to calculate a polynomial through the data is used

        // The list of coordinate x-values
        Vector<Double> x(nPrimes);
        indgen(x, 1.0);  // 1, 2, ..\.
        Vector<Double> primesTable(nPrimes);
        for (uInt i=1; i < nPrimes; i++) {
           primesTable(i) =
           Primes::nextLargerPrimeThan(Int(primesTable(i-1)+0.01));
         }   
        Vector<Double> sigma(nPrimes);
        sigma = 1.0;
        // The fitter
        LinearFit<Double> fitter;
        // Linear combination of functions describing 1 + x + x*x
        combination.setCoefficient(0, 1.0);   // 1
        combination.setCoefficient(1, 1.0);     // x
        combination.setCoefficient(2, 1.0);     // x^2
        // Get the solution
        fitter.setFunction(combination);
        Vector<Double> solution = fitter.fit(x, primesTable, sigma);
        // Try with a function with automatic derivatives (note that default 
        // polynomial has zero first guess)
        LinearFit<AutoDiffA<Double> > fitad;
        Polynomial<AutoDiffA<Double> > sqre(2);
        fitad.setFunction(sqre);
        solution = fitad.fit(x, primesTable, sigma);

In the test program examples are given on how to get the other information, and other examples.

Definition at line 214 of file GenericL2Fit.h.

Constructor & Destructor Documentation

template<class T>

casa::GenericL2Fit< T >::GenericL2Fit ( )

Create a fitter: the normal way to generate a fitter object.

Necessary data will be deduced from the Functional provided with setFunction()

template<class T>

casa::GenericL2Fit< T >::GenericL2Fit ( const GenericL2Fit< T > & other )

Copy constructor (deep copy)

template<class T>

virtual casa::GenericL2Fit< T >::~GenericL2Fit ( ) [virtual]

Destructor.

Member Function Documentation

template<class T>

Bool casa::GenericL2Fit< T >::addConstraint	(	const Function< typename FunctionTraits< T >::DiffType, typename FunctionTraits< T >::DiffType > &	function,
		const Vector< typename FunctionTraits< T >::BaseType > &	x,
		const typename FunctionTraits< T >::BaseType	y = `typename FunctionTraits< T >::BaseType(0)`
	)

template<class T>

Bool casa::GenericL2Fit< T >::addConstraint	(	const Vector< typename FunctionTraits< T >::BaseType > &	x,
		const typename FunctionTraits< T >::BaseType	y = `typename FunctionTraits< T >::BaseType(0)`
	)

template<class T>

Bool casa::GenericL2Fit< T >::addConstraint ( const typename FunctionTraits< T >::BaseType y = typename FunctionTraits< T >::BaseType(0) )

template<class T>

void casa::GenericL2Fit< T >::asSVD ( const Bool svd )

Set the use of SVD or not (default).

When set the default collinearity is set as well.

template<class T>

void casa::GenericL2Fit< T >::asWeight ( const Bool aswgt ) [inline]

Set sigma values to be interpreted as weight (i.e.

1/sigma/sigma). A value of zero or -1 will be skipped. The switch will stay in effect until set False again explicitly. Default is False.

Definition at line 289 of file GenericL2Fit.h.

template<class T>

void casa::GenericL2Fit< T >::buildConstraint ( ) [protected]

Build the constraint equations.

template<class T>

void casa::GenericL2Fit< T >::buildMatrix	(	const Array< typename FunctionTraits< T >::BaseType > &	x,
		const Vector< typename FunctionTraits< T >::BaseType > &	y,
		const Vector< typename FunctionTraits< T >::BaseType > *const	sigma,
		const Vector< Bool > *const	mask = `0`
	)		`[protected]`

Build the normal matrix.

template<class T>

void casa::GenericL2Fit< T >::buildNormalMatrix	(	const Vector< typename FunctionTraits< T >::BaseType > &	x,
		const Vector< typename FunctionTraits< T >::BaseType > &	y,
		const Vector< typename FunctionTraits< T >::BaseType > &	sigma,
		const Vector< Bool > *const	mask = `0`
	)

Generate the normal equations by one or more calls to the buildNormalMatrix(), before calling a fit() without arguments.

The arguments are the same as for the fit(arguments) function. A False is returned if the Array sizes are unmatched.

template<class T>

void casa::GenericL2Fit< T >::buildNormalMatrix	(	const Matrix< typename FunctionTraits< T >::BaseType > &	x,
		const Vector< typename FunctionTraits< T >::BaseType > &	y,
		const Vector< typename FunctionTraits< T >::BaseType > &	sigma,
		const Vector< Bool > *const	mask = `0`
	)

template<class T>

void casa::GenericL2Fit< T >::buildNormalMatrix	(	const Vector< typename FunctionTraits< T >::BaseType > &	x,
		const Vector< typename FunctionTraits< T >::BaseType > &	y,
		const Vector< Bool > *const	mask = `0`
	)

template<class T>

void casa::GenericL2Fit< T >::buildNormalMatrix	(	const Matrix< typename FunctionTraits< T >::BaseType > &	x,
		const Vector< typename FunctionTraits< T >::BaseType > &	y,
		const Vector< Bool > *const	mask = `0`
	)

template<class T>

Bool casa::GenericL2Fit< T >::buildResidual	(	Vector< typename FunctionTraits< T >::BaseType > &	y,
		const Array< typename FunctionTraits< T >::BaseType > &	x,
		const Vector< typename FunctionTraits< T >::BaseType > *const	sol,
		const Bool	model = `False`
	)		`[protected]`

Calculate residuals.

template<class T>

Double casa::GenericL2Fit< T >::chiSquare ( ) const [inline]

Obtain the chi squared.

It has already been calculated during the fitting process.

Definition at line 389 of file GenericL2Fit.h.

template<class T>

Matrix<Double> casa::GenericL2Fit< T >::compuCovariance ( )

Get covariance matrix.

template<class T>

void casa::GenericL2Fit< T >::compuCovariance ( Matrix< Double > & cov )

template<class T>

const Vector<typename FunctionTraits<T>::BaseType>& casa::GenericL2Fit< T >::errors ( ) const

Get the errors on the solved values.

Thrown Exceptions

AipsError if none present (or Bool returned)

template<class T>

Bool casa::GenericL2Fit< T >::errors ( Vector< typename FunctionTraits< T >::BaseType > & err ) const

template<class T>

void casa::GenericL2Fit< T >::fillSVDConstraints ( ) [protected]

Get the SVD constraints.

template<class T>

Vector<typename FunctionTraits<T>::BaseType> casa::GenericL2Fit< T >::fit	(	const Vector< typename FunctionTraits< T >::BaseType > &	x,
		const Vector< typename FunctionTraits< T >::BaseType > &	y,
		const Vector< typename FunctionTraits< T >::BaseType > &	sigma,
		const Vector< Bool > *const	mask = `0`
	)

Fit the function to the data.

If no sigma provided, all ones assumed. In the case of no x,y,sigma the fitting equations are supposed to be generated by previous calls to buildNormalMatrix. Note that the ones with a scalar sigma will assume sigma=1 (overloading problem). The mask assumes that if present, points with False will be skipped.

Thrown Exceptions

AipsError if unmatched array sizes given
AipsError if equations cannot be inverted (not in SVD case and in the case of the Bool versions.)

template<class T>

Vector<typename FunctionTraits<T>::BaseType> casa::GenericL2Fit< T >::fit	(	const Matrix< typename FunctionTraits< T >::BaseType > &	x,
		const Vector< typename FunctionTraits< T >::BaseType > &	y,
		const Vector< typename FunctionTraits< T >::BaseType > &	sigma,
		const Vector< Bool > *const	mask = `0`
	)

template<class T>

Vector<typename FunctionTraits<T>::BaseType> casa::GenericL2Fit< T >::fit	(	const Vector< typename FunctionTraits< T >::BaseType > &	x,
		const Vector< typename FunctionTraits< T >::BaseType > &	y,
		const Vector< Bool > *const	mask = `0`
	)

template<class T>

Vector<typename FunctionTraits<T>::BaseType> casa::GenericL2Fit< T >::fit	(	const Matrix< typename FunctionTraits< T >::BaseType > &	x,
		const Vector< typename FunctionTraits< T >::BaseType > &	y,
		const Vector< Bool > *const	mask = `0`
	)

template<class T>

Vector<typename FunctionTraits<T>::BaseType> casa::GenericL2Fit< T >::fit ( const Vector< Bool > *const mask = 0 )

template<class T>

Bool casa::GenericL2Fit< T >::fit	(	Vector< typename FunctionTraits< T >::BaseType > &	sol,
		const Vector< typename FunctionTraits< T >::BaseType > &	x,
		const Vector< typename FunctionTraits< T >::BaseType > &	y,
		const Vector< typename FunctionTraits< T >::BaseType > &	sigma,
		const Vector< Bool > *const	mask = `0`
	)

template<class T>

Bool casa::GenericL2Fit< T >::fit	(	Vector< typename FunctionTraits< T >::BaseType > &	sol,
		const Matrix< typename FunctionTraits< T >::BaseType > &	x,
		const Vector< typename FunctionTraits< T >::BaseType > &	y,
		const Vector< typename FunctionTraits< T >::BaseType > &	sigma,
		const Vector< Bool > *const	mask = `0`
	)

template<class T>

Bool casa::GenericL2Fit< T >::fit	(	Vector< typename FunctionTraits< T >::BaseType > &	sol,
		const Vector< typename FunctionTraits< T >::BaseType > &	x,
		const Vector< typename FunctionTraits< T >::BaseType > &	y,
		const typename FunctionTraits< T >::BaseType &	sigma,
		const Vector< Bool > *const	mask = `0`
	)

template<class T>

Bool casa::GenericL2Fit< T >::fit	(	Vector< typename FunctionTraits< T >::BaseType > &	sol,
		const Matrix< typename FunctionTraits< T >::BaseType > &	x,
		const Vector< typename FunctionTraits< T >::BaseType > &	y,
		const typename FunctionTraits< T >::BaseType &	sigma,
		const Vector< Bool > *const	mask = `0`
	)

template<class T>

Bool casa::GenericL2Fit< T >::fit	(	Vector< typename FunctionTraits< T >::BaseType > &	sol,
		const Vector< Bool > *const	mask = `0`
	)

template<class T>

virtual Bool casa::GenericL2Fit< T >::fitIt	(	Vector< typename FunctionTraits< T >::BaseType > &	sol,
		const Array< typename FunctionTraits< T >::BaseType > &	x,
		const Vector< typename FunctionTraits< T >::BaseType > &	y,
		const Vector< typename FunctionTraits< T >::BaseType > *const	sigma,
		const Vector< Bool > *const	mask = `0`
	)		`[protected, pure virtual]`

Generalised fitter.

Implemented in casa::LinearFit< T >, casa::LinearFit< Float >, casa::NonLinearFit< T >, casa::NonLinearFit< Double >, casa::NonLinearFitLM< T >, and casa::NonLinearFitLM< Double >.

template<class T>

Function<typename FunctionTraits<T>::DiffType, typename FunctionTraits<T>::DiffType>* casa::GenericL2Fit< T >::fittedFunction ( ) [inline]

Return a pointer to the function being fitted.

Should never delete this pointer.

Definition at line 299 of file GenericL2Fit.h.

template<class T>

const Function<typename FunctionTraits<T>::DiffType, typename FunctionTraits<T>::DiffType>* casa::GenericL2Fit< T >::fittedFunction ( ) const [inline]

Definition at line 303 of file GenericL2Fit.h.

template<class T>

uInt casa::GenericL2Fit< T >::fittedNumber ( ) const [inline]

Return the number of fitted parameters.

Definition at line 306 of file GenericL2Fit.h.

template<class T>

Function<typename FunctionTraits<T>::DiffType, typename FunctionTraits<T>::DiffType>* casa::GenericL2Fit< T >::getConstraint ( const uInt n ) [inline]

Definition at line 314 of file GenericL2Fit.h.

template<class T>

uInt casa::GenericL2Fit< T >::getRank ( ) const [inline]

Get the rank of the solution (or zero of no fit() done yet).

A valid solution will have the same rank as the number of unknowns (or double that number in the complex case). For SVD solutions the rank could be less.

Definition at line 455 of file GenericL2Fit.h.

template<class T>

Vector<typename LSQTraits<typename FunctionTraits<T>:: BaseType>::base> casa::GenericL2Fit< T >::getSVDConstraint ( uInt n )

Return the nth constraint equation derived from SVD Note that the number present will be given by getDeficiency()

template<class T>

FunctionTraits<T>::BaseType casa::GenericL2Fit< T >::getVal_p	(	const Array< typename FunctionTraits< T >::BaseType > &	x,
		uInt	j,
		uInt	i
	)		const `[protected]`

Function to get evaluated functional value.

template<class T>

void casa::GenericL2Fit< T >::initfit_p ( uInt parcnt ) [protected]

Initialise the fitter with number of solvable parameters.

template<class T>

uInt casa::GenericL2Fit< T >::NConstraints ( ) [inline]

Return the number of constraints, and pointers to constraint functions.

A 0-pointer will be returned if no such constraint present. This pointer should never be destroyed.

Definition at line 312 of file GenericL2Fit.h.

template<class T>

GenericL2Fit& casa::GenericL2Fit< T >::operator= ( const GenericL2Fit< T > & other )

Assignment (deep copy)

template<class T>

void casa::GenericL2Fit< T >::resetFunction ( ) [protected]

Reset all the input.

Referenced by casa::GenericL2Fit< DComplex >::setFunction().

template<class T>

Bool casa::GenericL2Fit< T >::residual	(	Vector< typename FunctionTraits< T >::BaseType > &	y,
		const Array< typename FunctionTraits< T >::BaseType > &	x,
		const Vector< typename FunctionTraits< T >::BaseType > &	sol,
		const Bool	model = `False`
	)

Return the residual after a fit in y.

x can be a vector (if 1D function) or a matrix (ND functional), as in the fit() methods. If sol is given, it is the solution derived from a fit and its value will be used; otherwise only the parameters in the fitted functional will be used. If model is given as True, the model, rather the residual <data>-<model> will be returned in y. False is returned if residuals cannot be calculated.

Thrown Exceptions

Aipserror if illegal array sizes

template<class T>

Bool casa::GenericL2Fit< T >::residual	(	Vector< typename FunctionTraits< T >::BaseType > &	y,
		const Array< typename FunctionTraits< T >::BaseType > &	x,
		const Bool	model = `False`
	)

template<class T>

void casa::GenericL2Fit< T >::setCollinearity ( const Double cln )

Set the collinearity factor as the square of the sine of the minimum angle allowed between input vectors (default zero for non-SVD, 1e-8 for SVD)

template<class T>

template<class U >

Bool casa::GenericL2Fit< T >::setConstraint	(	const uInt	n,
		const Function< U, U > &	function,
		const Vector< typename FunctionTraits< T >::BaseType > &	x,
		const typename FunctionTraits< T >::BaseType	y = `typename FunctionTraits<T>::BaseType(0)`
	)		`[inline]`

Set the possible constraint functions.

The addConstraint will add one; the setConstraint will [re-]set the nth constraint. If unsucessful, False returned.
Constraint functional can only be set when the function to be fitted has been set. It should have the same number of parameters as the function to be fitted. The x should have the correct dimension.

Definition at line 252 of file GenericL2Fit.h.

template<class T>

Bool casa::GenericL2Fit< T >::setConstraint	(	const uInt	n,
		const Vector< typename FunctionTraits< T >::BaseType > &	x,
		const typename FunctionTraits< T >::BaseType	y = `typename FunctionTraits< T >::BaseType(0)`
	)

template<class T>

Bool casa::GenericL2Fit< T >::setConstraint	(	const uInt	n,
		const typename FunctionTraits< T >::BaseType	y = `typename FunctionTraits< T >::BaseType(0)`
	)

template<class T>

Bool casa::GenericL2Fit< T >::setConstraintEx	(	const uInt	n,
		const Vector< typename FunctionTraits< T >::BaseType > &	x,
		const typename FunctionTraits< T >::BaseType	y
	)		`[private]`

Set Constraint properties.

Referenced by casa::GenericL2Fit< DComplex >::setConstraint().

template<class T>

template<class U >

void casa::GenericL2Fit< T >::setFunction ( const Function< U, U > & function ) [inline]

Sets the function to be fitted.

Upon entry, the argument function object is cloned. The cloned copy is used in the later fitting process. A valid function should be an instance of the Function class, so that derivatives with respect to the adjustable parameters can be calculated. The current values of the "available" parameters of the function are taken as the initial guess for the non-linear fitting.

Definition at line 241 of file GenericL2Fit.h.

template<class T>

void casa::GenericL2Fit< T >::setFunctionEx ( ) [private]

Set function properties.

Referenced by casa::GenericL2Fit< DComplex >::setFunction().

template<class T>

void casa::GenericL2Fit< T >::setMaskedParameterValues ( const Vector< typename FunctionTraits< T >::BaseType > & parms )

template<class T>

void casa::GenericL2Fit< T >::setParameterValues ( const Vector< typename FunctionTraits< T >::BaseType > & parms )

Set the parameter values.

The input is a vector of parameters; all or only the masked ones' values will be set, using the input values

template<class T>

uInt casa::GenericL2Fit< T >::testInput_p	(	const Array< typename FunctionTraits< T >::BaseType > &	x,
		const Vector< typename FunctionTraits< T >::BaseType > &	y,
		const Vector< typename FunctionTraits< T >::BaseType > *const	sigma
	)		`[protected]`

Return number of condition equations and check sizes x, y, sigma.

Thrown Exceptions

Aipserror if size inconsistencies

Member Data Documentation

template<class T>

uInt casa::GenericL2Fit< T >::aCount_ai [protected]

Adjustable.

Definition at line 461 of file GenericL2Fit.h.

Referenced by casa::GenericL2Fit< DComplex >::fittedNumber().

template<class T>

Vector<typename FunctionTraits<T>::ArgType> casa::GenericL2Fit< T >::arg_p [mutable, protected]

Contiguous argument areas.

Definition at line 501 of file GenericL2Fit.h.

template<class T>

Bool casa::GenericL2Fit< T >::asweight_p [protected]

Interpret as weights rather than as sigma the given values.

Definition at line 492 of file GenericL2Fit.h.

Referenced by casa::GenericL2Fit< DComplex >::asWeight().

template<class T>

Vector<typename FunctionTraits<T>::ArgType> casa::GenericL2Fit< T >::carg_p [mutable, protected]

Definition at line 502 of file GenericL2Fit.h.

template<class T>

const Double casa::GenericL2Fit< T >::COLLINEARITY

Default collinearity test for SVD.

Definition at line 218 of file GenericL2Fit.h.

template<class T>

Vector<typename FunctionTraits<T>::BaseType> casa::GenericL2Fit< T >::condEq_p [mutable, protected]

Condition equation parameters (for number of adjustable parameters)

Definition at line 496 of file GenericL2Fit.h.

template<class T>

PtrBlock<Vector<typename FunctionTraits<T>::BaseType>*> casa::GenericL2Fit< T >::constrArg_p [protected]

List of vectors describing the constraint equations' arguments.

Definition at line 476 of file GenericL2Fit.h.

template<class T>

PtrBlock<Function<typename FunctionTraits<T>::DiffType, typename FunctionTraits<T>::DiffType>*> casa::GenericL2Fit< T >::constrFun_p [protected]

List of functions describing the possible constraint equations e.g.

The sum of 3 angles w`could be described by a HyperPlane(3) function with [1,1,1] as parameters; giving [1,1,1] as argument vector and 3.1415 as value.

Definition at line 474 of file GenericL2Fit.h.

Referenced by casa::GenericL2Fit< DComplex >::getConstraint(), casa::GenericL2Fit< DComplex >::NConstraints(), and casa::GenericL2Fit< DComplex >::setConstraint().

template<class T>

PtrBlock<typename FunctionTraits<T>::BaseType *> casa::GenericL2Fit< T >::constrVal_p [protected]

List of values describing the constraint equations' value.

Definition at line 478 of file GenericL2Fit.h.

template<class T>

Vector<Vector<typename LSQTraits<typename FunctionTraits<T>:: BaseType>::base> > casa::GenericL2Fit< T >::consvd_p [mutable, protected]

Local SVD constraints.

Definition at line 518 of file GenericL2Fit.h.

template<class T>

Vector<typename FunctionTraits<T>::BaseType> casa::GenericL2Fit< T >::err_p [mutable, protected]

Local error area.

Definition at line 511 of file GenericL2Fit.h.

template<class T>

Bool casa::GenericL2Fit< T >::errors_p [protected]

Have errors.

Definition at line 489 of file GenericL2Fit.h.

template<class T>

Vector<typename FunctionTraits<T>::BaseType> casa::GenericL2Fit< T >::ferr_p [mutable, protected]

Definition at line 512 of file GenericL2Fit.h.

template<class T>

Bool casa::GenericL2Fit< T >::ferrors_p [mutable, protected]

Definition at line 490 of file GenericL2Fit.h.

template<class T>

Vector<typename FunctionTraits<T>::BaseType> casa::GenericL2Fit< T >::fsol_p [mutable, protected]

Definition at line 507 of file GenericL2Fit.h.

template<class T>

Vector<typename FunctionTraits<T>::BaseType> casa::GenericL2Fit< T >::fullEq_p [mutable, protected]

Equation for all available parameters.

Definition at line 498 of file GenericL2Fit.h.

template<class T>

uInt casa::GenericL2Fit< T >::ndim_p [protected]

Number of dimensions of input data.

Definition at line 483 of file GenericL2Fit.h.

template<class T>

Bool casa::GenericL2Fit< T >::needInit_p [protected]

No normal equations yet.

Definition at line 485 of file GenericL2Fit.h.

template<class T>

uInt casa::GenericL2Fit< T >::nr_p [protected]

The rank of the solution.

Definition at line 494 of file GenericL2Fit.h.

template<class T>

uInt casa::GenericL2Fit< T >::pCount_p [protected]

Number of available parameters.

Definition at line 481 of file GenericL2Fit.h.

template<class T>

Function<typename FunctionTraits<T>::DiffType, typename FunctionTraits<T>::DiffType>* casa::GenericL2Fit< T >::ptr_derive_p [protected]

Function to use in evaluating condition equation.

Definition at line 466 of file GenericL2Fit.h.

Referenced by casa::GenericL2Fit< DComplex >::fittedFunction(), casa::GenericL2Fit< DComplex >::setConstraint(), and casa::GenericL2Fit< DComplex >::setFunction().

template<class T>

Vector<typename FunctionTraits<T>::BaseType> casa::GenericL2Fit< T >::sol_p [mutable, protected]

Local solution area.

Reimplemented from casa::LSQFit.

Definition at line 506 of file GenericL2Fit.h.

template<class T>

Bool casa::GenericL2Fit< T >::solved_p [protected]

Have solution.

Definition at line 487 of file GenericL2Fit.h.

Referenced by casa::GenericL2Fit< DComplex >::getRank().

template<class T>

Bool casa::GenericL2Fit< T >::svd_p [protected]

SVD indicator.

Definition at line 463 of file GenericL2Fit.h.

template<class T>

FunctionTraits<T>::DiffType casa::GenericL2Fit< T >::valder_p [mutable, protected]

Local value and derivatives.

Definition at line 515 of file GenericL2Fit.h.

The documentation for this class was generated from the following file:

casacore/scimath/Fitting/GenericL2Fit.h

Public Member Functions

Public Attributes

Protected Member Functions

Protected Attributes

Private Member Functions

Detailed Description

template<class T> class casa::GenericL2Fit< T >

Review Status

Prerequisite

Etymology

Synopsis

Template Type Argument Requirements (T)

Motivation

Example

Constructor & Destructor Documentation

Member Function Documentation

Thrown Exceptions

Thrown Exceptions

Thrown Exceptions

Thrown Exceptions

Member Data Documentation

template<class T>
class casa::GenericL2Fit< T >