Getting Started

Documentation

Glish

Learn More

Programming

Contact Us

Version 1.9 Build 1367

News	FAQ
Search	Home

The Imaging Model

We have seen how the relation AI = D can describe the measurement equation of a telescope. This suggests that we think of AI = D as the Imaging Model. How is the Imaging Model to be used in a deconvolution algorithm? Many algorithms perform a least squares fit of a model to the data. For example, CLEAN does least squares fitting of sinusoids to the visibility data, while MEM does least squares fitting augmented by an entropy term. The $\chi^{2}_{}$ term can be written as:

$$\chi^{2}_{}$$ (8)

where w is inverse of the covariance matrix of errors. Often the errors are independent between data points, in which case w is diagonal with elements:

$${1\over \sigma^2_i}$$ (9)

There are two closely related approachs to using $\chi^{2}_{}$. First, we consider an approach based upon the idea of optimization: many iterative algorithms update an estimate of I based upon $\chi^{2}_{}$ and its gradient with respect to I:

$${\partial \chi^2\over\partial I}$$ (10)

We can define the services of the Imaging Model which are required evaluate this term:

1.

Use a service predict to find AI,

2.

Subtract D to get AI - D,

3.

Use a service invert to get 2A^Tw(AI - D)

The second approach is based on the normal equation. At the optimum solution I, the gradient of $\chi^{2}_{}$ must be zero and so we have that:

A^TwAI = A^TwD (11)

Note that in imaging, the normal equation sometimes becomes the convolution equation.

Only in rare cases can the normal equation be solved exactly and only in even rarer cases is it a good idea to do so (see Press et al., 1989). Often a better strategy is to make corrections to a trial image based upon the residual in this equation A^TwAI - A^TwD.

The normal equation probably warrants a service: residual, returning $\chi^{2}_{}$ and A^TwAI - A^TwD (which is also, conveniently, ${1\over 2}$${\partial \chi^2\over\partial I}$).

Some readers may feel that the distinction between these two approaches is subtle to the point of vanishing. Perhaps the best reason to make such a distinction is that the literature does. Both views are seen in published papers. The normal equation approach looks a bit simpler and avoids the worrying connotations of optimization theory. The optimization approach is more easily improved: for example, one could use conjugate gradients or variable metric algorithms for the optimization. In the rest of this document I will retain the distinction, principally to respect the original derivation of each algorithm.

Following Holdaway and Bhatnagar (1992), I will use the term Imager to denote any algorithm which estimates I from A and D and any extra information. Many existing Imagers fit one of these two approaches:

UVMAP

raises up a couple of interesting points. First, it does nothing to estimate vectors in the null space, and in fact, these are usually absent altogether. Second, the image produced by uvmap actually corresponds to A^TwD normalized by the diagonal element of A^TwA. It is obvious that this is a more satisfactory estimate of I than A^TwD alone. If A^TwA is diagonal then this is inverse of A. This estimate is probably worth making generally available as a service of the Imaging Model. This suggests that we extend the definition of solve: returns A^TwD for given D, optionally normalized by the diagonal elements of A^TwT. Also residual could be augmented in a similar way. We would also benefit from a service Hdiagonal which returns the diagonal elements of the Hessian matrix A^TwA.

Hogbom CLEAN

is appropriate for the interferometric Convolution Imaging Model. It operates on the normal equation residual by selecting the peak as an estimate of the strength and location of a point source increment to the current image. In this case, A is the full dirty beam and is therefore Toeplitz. We use the normalized solve to get the dirty image, and a new service, the normalized observe which returns A^TwAI, to get one row of the PSF where I^P is an appropriately centered point source.

Clark CLEAN

is also appropriate for the interferometric Convolution Imaging Model. The algorithm proceeds in minor and major cycles. In a minor cycle, a non-Toeplitz subsection of the dirty beam is used in a tightly written inner loop to clean only the high points of the residual image. In the major loop, the full Toeplitz dirty beam is used via zero-padding and an FFT-convolution. As mentioned above, one can regard this algorithm as the logical result of alternately using a sparse and then a circulant approximation for A.

MX

uses both the interferometric Convolution and the Interferometric Imaging Models. In the minor cycle, a sparse approximation for the Convolution A is used, while in the major cycle, multiplication by the Interferometric A is mimiced by using degridding and gridding together with an FFT.

Projection on Convex Sets

uses a projection operator $\cal {T}$ to project the normal equation residual into the space of feasible solutions. The update formula can be written as follows:

$$\cal {T} \left(\vphantom{ A^T w (D-AI^{(n)})}\right. \left.\vphantom{ A^T w (D-AI^{(n)})}\right)$$ (12)

where $\cal {T}$ is the projection operator. In some cases, it pays to apply the inverse of the diagonal terms of the Hessian:

$$\cal {T} \left(\vphantom{\left[{\rm diag}(A^T w A)\right]^{-1} A^T w (D-AI^{(n)})}\right. \left[\vphantom{{\rm diag}(A^T w A)}\right. \left.\vphantom{{\rm diag}(A^T w A)}\right]^{-1}_{} \left.\vphantom{\left[{\rm diag}(A^T w A)\right]^{-1} A^T w (D-AI^{(n)})}\right)$$ (13)

A simple example would be to increment the current estimate of I by the positive parts of the normal equation residual. The operator $\cal {T}$ then just passes the positive parts of the image. CLEAN is a POCS algorithm in which the projection operator just passes the maximum pixel. You may think that POCS is a fancy term for something quite obvious but there is a convergence proof and other mathematical machinery which is quite useful: see Youla (1974).

MEM

can be applied to any of the Imaging Models described above. It is usually implemented via an optimization algorithm. The algorithm in AIPS uses ${\partial \chi^2\over\partial I}$ together with the entropy gradient lnI^M - lnI to find the deconvolved image using an iterative scheme (see Cornwell and Evans, 1985), stopping when $\chi^{2}_{}$ reaches a set limit. The algorithm also requires the diagonal elements of A^TwA provided by Hdiagonal. The update formula is:

$$\gamma \left[\vphantom{{1\over I}+\alpha{\rm diag}(A^T w A)}\right. {1\over I} \alpha \left.\vphantom{{1\over I}+\alpha{\rm diag}(A^T w A)}\right]^{-1}_{} \left(\vphantom{\ln{I^M}-\ln{I^{(n)}} + \alpha A^T w (D-AI^{(n)})}\right. \alpha \left.\vphantom{\ln{I^M}-\ln{I^{(n)}} + \alpha A^T w (D-AI^{(n)})}\right)$$ (14)

where $\gamma$ and $\alpha$ are carefully chosen constants.

VTESS

applies to the Mosaic Imaging Model. It uses the sum of ${\partial \chi^2\over\partial I}$ for all pointings together with the entropy gradient lnI^M - lnI to find the mosaic image (see Cornwell 1988).

LTESS

(also known as linear mosaic) is an interesting case where the normalized solve service produces the solution to the normal equation. For the Primary Beam Tapering Imaging Model described above, the normalized solve returns:

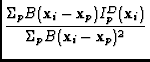
$$\bf x_{i}^{} {\Sigma_p B({\bf x}_i-{\bf x}_p) I^D_{p}({\bf x}_i) \over \Sigma_p B({\bf x}_i-{\bf x}_p)^2}$$ (15)

where I^D_p is the dirty image for pointing position $\bf x_{p}^{}$ and the summation is over all pointing centers. This algorithm has two uses, first for low SNR images where the sidelobes of the synthesized beam are unimportant, and second for adding residuals back to the result of non-linear mosaic.

In all these Imagers, the Imaging Model is separated out in a very clean way. For example, MEM needs only to call two services of the Imaging Model: residual and Hdiagonal. An interesting question is whether all Imagers call Imaging Models directly. The only possible exception is the Högbom CLEAN where the point spread function A^TwAI^P is cached and used in an inner loop. This split is really a semantic one only since one could envisage a program which took a visibility dataset and made the dirty image A^TwD and the dirty beam A^TwAI^P directly and then proceeded to the CLEAN step without writing either to disk. We therefore conclude that in essence all Imagers call upon services of Imaging Models. In some case, many different Imaging Models can be invoked. For example, the non-linear mosaic algorithm can potentially call the residual service of many different Imaging Models: Interferometric, Total Power, Beam-Switched Total Power, etc.

Note that as well as being able to compute the effect of A, we also need to be able to compute the effect of the transpose of A. This is usually quite straightforward and computationally efficient.

Convolution

A^T represents convolution by a shift-invariant spread function after inversion through the origin:

$$\bf x_{j}^{}$$ (16)

Interferometer

A^T is a matrix performing a Fourier sum:

$$\pi \bf u_{i} \bf x_{j}$$ (17)

Total Power

$$\bf x_{j}^{} \bf x_{i}^{}$$ (18)

Beam Switched Total Power

$$\bf x_{j}^{} \bf x_{i}^{} \bf x_{j}^{} \bf x_{i}^{} \Delta \bf x$$ (19)

Mosaic

A^T is a matrix representing Fourier transformation followed by multiplication by a primary beam centered at a specific fixed pointing position $\bf x^{p}_{}$:

$$\bf x_{j}^{} \bf x^{p}_{} \pi \bf u_{i} \bf x_{j}$$ (20)

Mosaic with variable pointing

A^T is a matrix representing Fourier transformation followed by multiplication by a primary beam centered at a variable pointing position $\bf x^{p}_{}$:

$$\bf x_{j}^{} \bf x^{p}_{i} \pi \bf u_{i} \bf x_{j}$$ (21)

Wide field transform

A^T is a matrix like that for the interferometer but including the w phase term.