
 News News |
 FAQ FAQ
|
 Search Search
|
 Home Home
|
| Getting Started | Documentation | Glish | Learn More | Programming | Contact Us |

| Version 1.9 Build 1367 |
|
My discussion of Imaging Model could be applied to any linear system of equations. Is calibration linear? I can think of three levels of difficulty in calibration:
| gigj* = Xij | (1) |
Hence my conclusion is that calibration can range from cases where linear algebra works, to cases where full non-linear optimization is required.
Extending the linear equations used in Imaging, we could say that the
observed data D is a function of a set of unknown parameters P and
some ``correct'' data
![]() . We then have that:
. We then have that:
|
D = C( |
(2) |
where C is now a general non-linear function. Given the
parameters P, we can predict the data perfectly. The two interesting
problems are, first, the inverse problem of deriving P from
knowledge of the functional form of C, measurements of the
data vector D and a prediction of
![]() perhaps from the
Imaging Model
perhaps from the
Imaging Model
![]() = AI, and, second, deriving
= AI, and, second, deriving
![]() for real
observations.
for real
observations.
Note that we could introduce the Imaging Model explicitly by writing, instead, a relation involving the image I and the matrix A:
| D = C(AI, P) | (3) |
However, I think that this is not worthwhile at this point and so for
the moment I will continue with writing
![]() for AI. I will
return to this point later when I discuss algorithms in more detail.
for AI. I will
return to this point later when I discuss algorithms in more detail.
Turning to the issue of how to solve equations of this type,
we can define a ![]() term to be minimized in order to derive P:
term to be minimized in order to derive P:
|
|
(4) |
where w is inverse of the covariance matrix of errors. If the errors are independent between data points, then w is diagonal with elements:
|
wi, i = |
(5) |
We consider an approach to solving for the P parameters based upon
the idea of optimization: many iterative algorithms update an estimate
of P based upon ![]() and its gradient with respect to P:
and its gradient with respect to P:
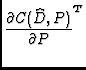 w(C( w(C( |
(6) |
As before, we can require the services of the Telescope model to calculate this term:
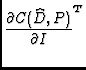 w(C( w(C( |
(7) |
So far, this is all quite obvious but is it helpful? One could imagine feeding this Telescope Model to a non-linear least-squares Solver in the same way that Imaging Model was fed to an Imager. I can think of several objections to this scheme.
The overwhelming conclusion is that the scheme I proposed for the Imaging Model cannot be easily extended to non-linear functions such as that found in calibration. The answer to the first question (``can we abstract the calibration of Telescopes into an equation part and a solver part?'') is No.