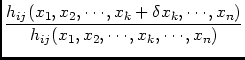Version 1.9 Build 1556

News	FAQ
Search	Home

Next: Bibliography Up: Some practical aspects of the matrix-based MEASUREMENT EQUATION Previous: IMPLEMENTATION IN AIPS++

A GENERALISED SOLVER

The elegance of the matrix formalism opens the way for a generalised non-linear complex Solver for the parameters of the Measurement Model (MM) and the Sky Model (SM). Such a solver can be used for any telescope that can be described with the formalism.

The full Measurement Equation expressed by 18 and 19 can be written as:

$\displaystyle \left(\vphantom{\begin{array}{c} v_{\rm pp}\\ v_{\rm pq}\\ v_{\rm qp}\\ v_{\rm qq} \end{array}}\right.$ $\displaystyle \begin{array}{c} v_{\rm pp}\\ v_{\rm pq}\\ v_{\rm qp}\\ v_{\rm qq} \end{array}$ $\displaystyle \left.\vphantom{\begin{array}{c} v_{\rm pp}\\ v_{\rm pq}\\ v_{\rm qp}\\ v_{\rm qq} \end{array}}\right)$ = $\displaystyle \vec{H}\,$ $\displaystyle \left(\vphantom{\begin{array}{c} I\\ Q\\ U\\ V \end{array}}\right.$ $\displaystyle \begin{array}{c} I\\ Q\\ U\\ V \end{array}$ $\displaystyle \left.\vphantom{\begin{array}{c} I\\ Q\\ U\\ V \end{array}}\right)$

(21)

The matrix coefficients h_ij of the `system matrix' $\vec{H}\,$ are functions h_ij(x₁, x₂, x₃,..., x_n) of the (complex) variables x_k. In general, these functions will be non-linear. For small variations $\Delta$ x_k:

$\displaystyle \Delta$ h_ij = $\displaystyle \sum_{k=1}^{n}$ $\displaystyle {\frac{\partial h_{ij}}{\partial x_{k}}}$ $\displaystyle \Delta$ x_k

(22)

Assuming that our Sky Model is correct, the uv-data are the result of multiplication with the true values of the h_ij:

v_pp^dat = h₁₁^true I^mod + h₁₂^true Q^mod + h₁₃^true U^mod + h₁₄^true V^mod

(23)

The uv-model values have been calculated from the Sky Model by multiplying them with the current values of the h_ij, i.e. the values that are obtained by using the best available values of the variables x_k:

v_pp^mod = h₁₁^curr I^mod + h₁₂^curr Q^mod + h₁₃^curr U^mod + h₁₄^curr V^mod

(24)

So, a `Selfcal equation' can be written in terms of a linear combination of the increments 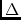$\Delta$ x_k, which would move the current values of the variables x_k closer to the true values:

v_pp^dat - v_pp^mod = (h₁₁^true - h₁₁^curr) I^mod + 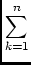^... = $\displaystyle \sum_{k=1}^{n}$ c_k $\displaystyle \Delta$ x_k

(25)

in which,

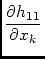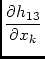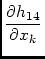c_k = $\displaystyle {\frac{\partial h_{11}}{\partial x_{k}}}$ I^mod + $\displaystyle {\frac{\partial h_{12}}{\partial x_{k}}}$ Q^mod + $\displaystyle {\frac{\partial h_{13}}{\partial x_{k}}}$ U^mod + $\displaystyle {\frac{\partial h_{14}}{\partial x_{k}}}$ V^mod

(26)

The `sensitivity' of h_ij for a variation in a variable x_k can be approximated by calculating the change in h_ij as result of a small `trial' variation 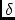$\delta$ x_k:

$\displaystyle {\frac{\partial h_{ij}}{\partial x_{k}}}$ $\displaystyle \approx$ $\displaystyle {\frac{h_{ij}(x_{1},x_{2},\cdots,x_{k}+\delta x_{k},\cdots,x_{n})}{h_{ij}(x_{1},x_{2},\cdots,x_{k}, \cdots,x_{n})}}$

(27)

These sensitivities will be different for different telescopes, due to the different values of the elements of the instrumental matrices etc. But given these matrices, they can be readily calculated.

The procedure can be further generalised to the case where better values have to be estimated for the parameters of the Sky Model.

The solving procedure would be as follows:

1.: Make sure that the parametrised instrumental matrices G,D,C,B,P,F and a parametrised Sky Model (SM) are available.
2.: Choose which of the parameters are variables to be solved, and which are assumed to be known values. The latter may also be expressions, like the parallactic angle.
3.: Supply extra constraints on the variables, in the form of extra equations. Example: solve for phase gradients over the array, rather than individual antenna phases.
4.: Feed it all to a symbolic processor which sets up the solution in an efficient way. It is important that most of the overhead that is caused by the generality goes into setting up the solver, and is not repeated for each MS row.
5.: Solve for the specified variables x_k, or rather their increments 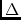$\Delta$ x_k. NB: The Solver should utilise a least-squares method (like SVD) that can deal automatically with situations in which there are too few constraints for a solution.
6.: After each solution, the estimated values 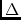$\Delta$ x_k are added to the values of the x_k in the relevant Correctors. These are used to create the starting point of new solutions.
7.: Iterate until some criterion is met. Iteration can also mean that one the Solver alternates between two sets of variables, or that an improved Sky Model is obtained inside the loop.

Next: Bibliography Up: Some practical aspects of the matrix-based MEASUREMENT EQUATION Previous: IMPLEMENTATION IN AIPS++ Contents