
| Version 1.9 Build 1367
|
|



Next: Calibration of the visibility
Up: The Generic Interferometer: I Overview of Calibration and
Previous: Introduction
I will restate the HBS measurement equation as described by Noordam
but with a few additions and simplifications to clarify the physical
content of the equation. In addition, I wish to correct what I believe
to be mistakes and omissions in his formulation.
A Generic Interferometer measures cross correlations between two
channels per feed, leading to a four-term cross-correlation that we
write as a vector, 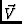 , subscripted by the pair of feeds
i, j:
, subscripted by the pair of feeds
i, j:
This basic measureable can be decomposed as follows. The measured
cross-correlation 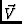 is given by:
is given by:
where Gi, Di, Ci
are 2 by 2 matrices representing specific feed-based effects. The
operator 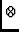 represents a direct matrix product yielding in this
case 4 by 4 matrices. Gi represents the complex gain of
the i'th feed, Di the leakage, and Ci is
a fixed matrix representing the nominal feed configuration. Noordam
gives examples of these terms. The terms
represents a direct matrix product yielding in this
case 4 by 4 matrices. Gi represents the complex gain of
the i'th feed, Di the leakage, and Ci is
a fixed matrix representing the nominal feed configuration. Noordam
gives examples of these terms. The terms
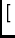 Gi
Gi 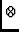 G*j
G*j![$ \left.\vphantom{{{G}_i\otimes{G}^*_j}}\right]$](img16.gif) ,
,
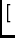 Di
Di 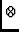 D*j
D*j![$ \left.\vphantom{{{D}_i\otimes{D}^*_j}}\right]$](img18.gif) , and
, and
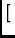 Ci
Ci 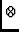 C*j
C*j![$ \left.\vphantom{{{C}_i\otimes{C}^*_j}}\right]$](img20.gif) are 4 by 4 matrices, and thus the
formulation is 4-dimensional. Physically the matrices
Gi, Di, Ci represent
coupling between the two polarization states for each feed and so the
terms
are 4 by 4 matrices, and thus the
formulation is 4-dimensional. Physically the matrices
Gi, Di, Ci represent
coupling between the two polarization states for each feed and so the
terms
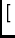 Gi
Gi 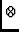 G*j
G*j![$ \left.\vphantom{{{G}_i\otimes{G}^*_j}}\right]$](img16.gif) ,
,
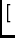 Di
Di 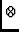 D*j
D*j![$ \left.\vphantom{{{D}_i\otimes{D}^*_j}}\right]$](img18.gif) ,
,
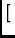 Ci
Ci 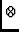 C*j
C*j![$ \left.\vphantom{{{C}_i\otimes{C}^*_j}}\right]$](img20.gif) represent coupling
between the four polarization correlation states. In appendix A, I
give a catalog of various forms for the calibration matrices.
represent coupling
between the four polarization correlation states. In appendix A, I
give a catalog of various forms for the calibration matrices.
A hint on reading these and succeeding equations: to get the
more usual equations, just convert matrices to scalars, ignore the
transposes, and convert the direct matrix product to a simple
product. The equations derived below should then look quite familiar.
The vector
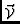 represents the visibility that would be
measured in the absence of the visibility-domain calibration effects.
1
represents the visibility that would be
measured in the absence of the visibility-domain calibration effects.
1
This includes only image-domain calibration effects. Thus, the feed-based
effects must now be a function of direction,
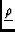 .
.
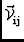 =
= 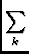 |
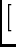 Ei Ei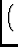 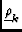
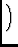
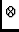 E*j
E*j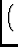 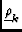
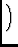 ![$\displaystyle \left.\vphantom{{{E}_i {\left(\underline{\rho}_k\right)} \otimes
{E}^*_j{\left(\underline{\rho}_k\right)}}}\right]$](img32.gif)  Pi Pi 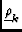
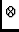 P*j
P*j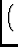 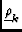
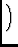 ![$\displaystyle \left.\vphantom{{{P}_i {\left(\underline{\rho}_k\right)} \otimes
{P}^*_j{\left(\underline{\rho}_k\right)}}}\right]$](img34.gif)  Fi Fi 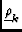
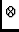 F*j
F*j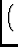 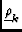
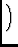 ![$\displaystyle \left.\vphantom{{{F}_i {\left(\underline{\rho}_k\right)} \otimes
{F}^*_j{\left(\underline{\rho}_k\right)}}}\right]$](img36.gif) |
|
|
| |
S 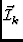 e-2 e-2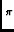 i i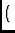 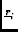 - -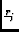 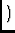 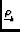 |
|
(4) |
where
Ei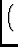
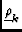
 represents the feed voltage
receptivity pattern of the i'th feed (Noordam used B for this
term),
Pi
represents the feed voltage
receptivity pattern of the i'th feed (Noordam used B for this
term),
Pi
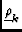
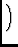 parallactic angle rotation, and
Fi
parallactic angle rotation, and
Fi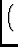
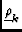
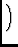 atmospheric terms including tropospheric and
ionospheric phase (Noordam used this term for Faraday rotation alone; here I
note that Faraday rotation can also be accomodated in F).
The term
atmospheric terms including tropospheric and
ionospheric phase (Noordam used this term for Faraday rotation alone; here I
note that Faraday rotation can also be accomodated in F).
The term
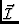 represents the polarized sky brightness. In the
Stokes representation, this is given by:
represents the polarized sky brightness. In the
Stokes representation, this is given by:
The matrix S converts from the representation used in
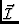 to
that most naturally used in describing the interferometer. HBS
use linear polarization as the canonical representation, for which the
S-matrix is:
to
that most naturally used in describing the interferometer. HBS
use linear polarization as the canonical representation, for which the
S-matrix is:
It is worth emphasizing that this is an arbitary choice and that one could,
instead, use circular polarization, in which case the S-matrix would be:
It may seem that Ci and S are redundant since one can
choose S so that Ci is a unit matrix. However, I
follow HBS and choose S to be the canonical Slin. Consequently,
Ci must be allowed to vary to suit the actual
measurement scheme of the feed. This flexibility is required for a
system of interferometers in which a mixture of linear and circular
polarization is measured. Note that the calibration matrices will then
inevitably be more complicated than would be the case if a single,
natural representation was used.
To emphasize the true glory of the full measurement equation, here I
give the whole expression:
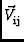 =
= |
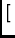 Gi Gi 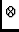 G*j
G*j![$\displaystyle \left.\vphantom{{{G}_i\otimes{G}^*_j}}\right]$](img8.gif) 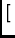 Di Di 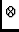 D*j
D*j![$\displaystyle \left.\vphantom{{{D}_i\otimes{D}^*_j}}\right]$](img10.gif) 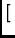 Ci Ci 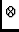 C*j
C*j![$\displaystyle \left.\vphantom{{{C}_i\otimes{C}^*_j}}\right]$](img12.gif) |
|
|
| |
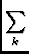  Ei Ei 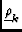
 E*j
E*j 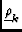
 ![$\displaystyle \left.\vphantom{{{E}_i {\left(\underline{\rho}_k\right)} \otimes
{E}^*_j{\left(\underline{\rho}_k\right)}}}\right]$](img32.gif)  Pi Pi 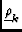
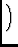
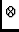 P*j
P*j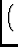 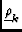
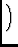 ![$\displaystyle \left.\vphantom{{{P}_i {\left(\underline{\rho}_k\right)} \otimes
{P}^*_j{\left(\underline{\rho}_k\right)}}}\right]$](img34.gif) 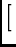 Fi Fi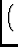 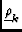
 F*j
F*j 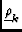
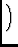 ![$\displaystyle \left.\vphantom{{{F}_i {\left(\underline{\rho}_k\right)} \otimes
{F}^*_j{\left(\underline{\rho}_k\right)}}}\right]$](img36.gif) |
|
|
| |
S 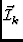 e-2 e-2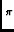 i i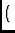 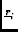 - -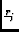 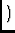 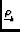 |
|
(8) |
It is worth making a number of comments about this very general form of
the measurement equation:
- Ordering of terms
- The ordering of terms follows the signal
path, reading right to left in the equation.
- Linearity
- The ME is linear in the sky brightness
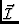 .
It is almost always non-linear in various calibration parameters.
This will have implications for solvers, as I discuss below.
.
It is almost always non-linear in various calibration parameters.
This will have implications for solvers, as I discuss below.
- Time and Frequency
- The formalism as presented here ignores indexing
by time and frequency. Both of these are trivial to add but obscure
the notation. Averaging over both time and frequency is then
accomodated easily.
- No new physics
- There is no new physics in this formulation.
The equations are totally equivalent to those derived earlier
(see e.g. Schwab, 1984). However, I expect that the
formulation will suggest new forms of calibration and imaging.
- Use of these equations
- In general, one will want to
determine one or both of the calibration parameters and the sky
brightness. To determine the calibration, one will fix the sky brightness
model, and solve for the calibration parameters, perhaps by a least squares
approach. The determine the sky brightness, one will want to fix the
calibration parameters and solve for the sky brightness, using
a deconvolution algorithm. One could alternate between calibration and
sky brightness estimation, as is done in most self-calibration
procedures, or one could do a joint solution by some very powerful
least squares type algorithm.
- Analytical forms for
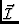
- In the calibration cycle, one will
have to perform an integration over
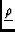 .
This will in general be quite difficult and usually, the
integration will have to be performed numerically. The ``art'' of
programming this equation will principally be in finding quick methods
of numerical integration using, for example, FFTs.
.
This will in general be quite difficult and usually, the
integration will have to be performed numerically. The ``art'' of
programming this equation will principally be in finding quick methods
of numerical integration using, for example, FFTs.
- Non-invertibility
- The ME is clearly not invertible for either the
sky brightness or the calibration matrices. This is really
a truism since it represents only one sample.
- Self-cal assumption
- The fundamental assumption yielding the direct
products is that all these instrumental effects factorize per
feed. It is hard to think of any exceptions to this, apart from
problems with the correlation process itself. Note that failure of
closure due to different bandpasses at the different feeds is
actually accomodated by the summation over frequency.
- Non-isoplanatism
- The location of the atmospheric phase terms is
actually ambiguous in most cases. Physically it belongs with the F term.
In isoplanatic conditions, it cannot be distinguished easily from
the electronic term G, and so it is usually written as belonging in
G. However, if the atmosphere is non-isoplanatic then the atmospheric
phase must be included in the F-term. F then actually decomposes a
follows:
- Assumption of perfect correlation
- Note that the correlation process
itself introduces errors that must be corrected, such as the van Vleck
correction. These we ignore for the moment.
- Completeness of information
- It is assumed that the full 4-dimensional
visibility is measured. In many cases, this is not so and, for example,
only the parallel hands will be correlated. Full correction is not
then possible but one expects that good approximations will be obtained
in many cases simply by inserting zeroes in the appropriate 4-vectors.
A similar but distinct difficulty arises in those interferometers that
measure different hands at different times. Such wrinkles can be dealt
with straightforwardly but further discussion is deferred to a
specifications document.



Next: Calibration of the visibility
Up: The Generic Interferometer: I Overview of Calibration and
Previous: Introduction
Contents
Please send questions or comments about AIPS++ to aips2-request@nrao.edu.
Copyright © 1995-2000 Associated Universities Inc.,
Washington, D.C.
Return to AIPS++ Home Page
2006-03-28

 News
News  FAQ
FAQ
 Search
Search
 Home
Home

![]() , subscripted by the pair of feeds
i, j:
, subscripted by the pair of feeds
i, j:
![]() is given by:
is given by:
![]() represents a direct matrix product yielding in this
case 4 by 4 matrices. Gi represents the complex gain of
the i'th feed, Di the leakage, and Ci is
a fixed matrix representing the nominal feed configuration. Noordam
gives examples of these terms. The terms
represents a direct matrix product yielding in this
case 4 by 4 matrices. Gi represents the complex gain of
the i'th feed, Di the leakage, and Ci is
a fixed matrix representing the nominal feed configuration. Noordam
gives examples of these terms. The terms
![]() Gi
Gi ![]() G*j
G*j![]() ,
,
![]() Di
Di ![]() D*j
D*j![]() , and
, and
![]() Ci
Ci ![]() C*j
C*j![]() are 4 by 4 matrices, and thus the
formulation is 4-dimensional. Physically the matrices
Gi, Di, Ci represent
coupling between the two polarization states for each feed and so the
terms
are 4 by 4 matrices, and thus the
formulation is 4-dimensional. Physically the matrices
Gi, Di, Ci represent
coupling between the two polarization states for each feed and so the
terms
![]() Gi
Gi ![]() G*j
G*j![]() ,
,
![]() Di
Di ![]() D*j
D*j![]() ,
,
![]() Ci
Ci ![]() C*j
C*j![]() represent coupling
between the four polarization correlation states. In appendix A, I
give a catalog of various forms for the calibration matrices.
represent coupling
between the four polarization correlation states. In appendix A, I
give a catalog of various forms for the calibration matrices.
![]() represents the visibility that would be
measured in the absence of the visibility-domain calibration effects.
1
represents the visibility that would be
measured in the absence of the visibility-domain calibration effects.
1
![]() .
.
![]()
![]()
![]() represents the feed voltage
receptivity pattern of the i'th feed (Noordam used B for this
term),
Pi
represents the feed voltage
receptivity pattern of the i'th feed (Noordam used B for this
term),
Pi![]()
![]()
![]() parallactic angle rotation, and
Fi
parallactic angle rotation, and
Fi![]()
![]()
![]() atmospheric terms including tropospheric and
ionospheric phase (Noordam used this term for Faraday rotation alone; here I
note that Faraday rotation can also be accomodated in F).
The term
atmospheric terms including tropospheric and
ionospheric phase (Noordam used this term for Faraday rotation alone; here I
note that Faraday rotation can also be accomodated in F).
The term
![]() represents the polarized sky brightness. In the
Stokes representation, this is given by:
represents the polarized sky brightness. In the
Stokes representation, this is given by:
![]() to
that most naturally used in describing the interferometer. HBS
use linear polarization as the canonical representation, for which the
S-matrix is:
to
that most naturally used in describing the interferometer. HBS
use linear polarization as the canonical representation, for which the
S-matrix is: