
 News News |
 FAQ FAQ
|
 Search Search
|
 Home Home
|
| Getting Started | Documentation | Glish | Learn More | Programming | Contact Us |

| Version 1.9 Build 1367 |
|
Since the connection between estimating the sky brightness and
deconvolution is becoming less and less straightforward as our
approaches gain in sophistication, I will use the term Image
Solver for what we previously called a deconvolution algorithm. An
Image Solver estimates the sky brightness
![]() for a fixed set of
calibration matrices. The principal algorithms that we need to
accomodate are CLEAN and MEM. However, there should be flexibility
sufficient to allow other algorithms. I will assume that all image
solvers need:
for a fixed set of
calibration matrices. The principal algorithms that we need to
accomodate are CLEAN and MEM. However, there should be flexibility
sufficient to allow other algorithms. I will assume that all image
solvers need:
The main point of this memo is to take this definition and demonstrate that it does indeed fit nearly all of the image solvers that we now use. This is convenient since it provides a simple interface between an image solver and the machinery for the measurement equation. A well-defined interface is useful for designing software but it is also helpful in understanding algorithms. Thus this memo should address both subjects.
As shown in the first memo:
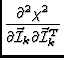 =
= |
2 |
||
| Wij/TD> | |||
| S | (3) |
It is not immediately obvious how to construct dirty and residual images
for this measurement equation, since the Fourier inverse does not apply.
Actually it is not clear just what a dirty image is supposed to be.
I argued previously that a good definition of a generalized dirty
image
![]() is:
is:
Note that the first term on the RHS of this equation is the inverse of a 4 by 4 matrix. By inverting this matrix, we are correcting for the coupling of different polarizations in the interferometer. By ignoring the non-diagonal terms of the Hessian, we are ignoring the coupling between different pixels in the final image. This is reasonable since, first, the coupling is singular, and, second, it is the role of an Image Solver to correct for this coupling.
A generalized residual image can be similarly defined as the
update direction for a given estimate of the sky brightness,
![]() .
Thus, as is reasonable, the residual image tends towards zero as the
model image reproduces the observed visibility data. Note that since
the residual image is defined in terms of the gradients and Hessian,
these are the primary interface to the measurement equation.
In fact, it makes good sense to think of residual image as an
image solver of status no different from any other image solver.
.
Thus, as is reasonable, the residual image tends towards zero as the
model image reproduces the observed visibility data. Note that since
the residual image is defined in terms of the gradients and Hessian,
these are the primary interface to the measurement equation.
In fact, it makes good sense to think of residual image as an
image solver of status no different from any other image solver.
In addition, there is a PSF
B(![]() ,
,![]() ) associated with the
generalized dirty image. Conceptually, it is calculated by propagating
an appropriately centered point source, at position
) associated with the
generalized dirty image. Conceptually, it is calculated by propagating
an appropriately centered point source, at position
![]() through
the measurement equation to obtain the predicted visibility and then
back into the image plane, to position
through
the measurement equation to obtain the predicted visibility and then
back into the image plane, to position
![]() , via the equation for
the dirty image. Thus the PSF is not necessarily shift-invariant.
Note also that the PSF is a (4 by 4) matrix for each point in
(
, via the equation for
the dirty image. Thus the PSF is not necessarily shift-invariant.
Note also that the PSF is a (4 by 4) matrix for each point in
(![]() ,
,![]() ) space (!) while the dirty and residual images are
images in which each pixel is a 4-vector. This means that any image
solver must estimate a 4-vector at every pixel, and that finding the
PSF requires evaluating the response separately for the 4 basis
vectors (e.g. once for each of I, Q, U, V). The Stokes parameters,
I, Q, U, V are therefore coupled together both in the calibration and
in the solution for the image. Note that the ``normal'' approach to
imaging is to correct coupling between Stokes parameters in the
measurements and then to deconvolve separately. Here the decoupling
and deconvolution are done simultaneously. At this point, it may be a
good idea to reassure the reader that conventional imaging can
be acheived using this formalization by making the appropriate
approximations: e.g. the PSF matrix is diagonal and
shift-invariant, in which case one is justified in using a
straightforward application of CLEAN to each of I, Q, U, V.
) space (!) while the dirty and residual images are
images in which each pixel is a 4-vector. This means that any image
solver must estimate a 4-vector at every pixel, and that finding the
PSF requires evaluating the response separately for the 4 basis
vectors (e.g. once for each of I, Q, U, V). The Stokes parameters,
I, Q, U, V are therefore coupled together both in the calibration and
in the solution for the image. Note that the ``normal'' approach to
imaging is to correct coupling between Stokes parameters in the
measurements and then to deconvolve separately. Here the decoupling
and deconvolution are done simultaneously. At this point, it may be a
good idea to reassure the reader that conventional imaging can
be acheived using this formalization by making the appropriate
approximations: e.g. the PSF matrix is diagonal and
shift-invariant, in which case one is justified in using a
straightforward application of CLEAN to each of I, Q, U, V.
Let us now consider how to use a priori information that applies
to the 4-vector
![]() .
.