Version 1.9 Build 1367

News	FAQ
Search	Home

Next: Comments Up: The Generic Interferometer: II Image Solvers AIPS++ Implementation Previous: CLEAN

Model fitting

It is common to want to represent 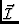$\vec{\cal I}\,$ by a set of discrete components such as Gaussians. If so, then the optimization would require gradients and the Hessian with respect to the parameters of the components rather than the pixel strengths as assumed above. Thus a model-fitter does not fit my simple definition of an Image Solver as that requires either a residual image or the gradient and inverse of the diagonal elements of the Hessian. It is important to understand the origin of this failing. It arises because the measurement equation is really an integral of complicated form that requires in most cases numerical integration. Consider, for example, a Gaussian observed by an interferometer with empirically determined primary beam patterns. In general there will not be an analytic expression for the predicted visibility and so it will be necessary to use numerical integration. The pixels in an image can then be viewed as a mechanism for numerical integration of the Measurement Equation. Hence one can use Gaussian models but I think that one is lead to numerical integration and hence the use of a pixellated image in conjunction with the chain rule. One can think of special cases that are exceptions (e.g. when a Gaussian is smaller in angular size than any of the size scales of the image plane calibration matrices, but in general numerical methods will be required.

Next: Comments Up: The Generic Interferometer: II Image Solvers AIPS++ Implementation Previous: CLEAN Contents