Version 1.9 Build 1367

News	FAQ
Search	Home

ATCA Calibration requirements for AIPS++
AIPS++ User Specification Memo 117

M.H. Wieringa

1995/07/18

Introduction

Currently, most calibration needs for the Compact Array are covered by the calibration routines in the Miriad package, written by Bob Sault. In this document I will summarize the available algorithms and some obvious extensions that AIPS++ would be expected to provide. I will not venture into any `exotic' calibration schemes or image plane corrections at this stage, but restrict this to what we would need to allow users to switch from Miriad to AIPS++ for their ATCA processing. This document uses the terminology of Jan Noordam's AIPS++ note 182.

The Miriad model

Bob Sault has given a one-page outline of Miriad visibility corrections as part of the Dwingeloo UVCI effort, I summarize that here.

Miriad models the transformation of true sky visibility to observed visibility using the following, `antenna-based' gain function:

g_p(t)g_p( $\displaystyle \nu$ ) $\displaystyle \left(\vphantom{{\nu\over\nu_0}}\right.$ $\displaystyle {\nu\over\nu_0}$ $\displaystyle \left.\vphantom{{\nu\over\nu_0}}\right)^{\alpha(t)}_{}$ exp(2 $\displaystyle \pi$ i $\displaystyle \tau$ (t)( $\displaystyle \nu$ - $\displaystyle \nu_{0}^{}$ )).

(1)

Here g_p(t) is the frequency independent, time variable gain for IF-channel p; g_p( $\nu$ ) is the time independent bandpass function for IF-channel p; the $\alpha$ (t) term models time dependent attenuation with a power law dependence on frequency; and $\tau$ (t) is a frequency and polarization independent, time variable delay. The latter two terms are seldom used. The terminology here is still a problem: antenna-based gains are really the gains associated with a single IF-channel in a single antenna, possibly but not necessarily associated with a single receptor (e.g., X-dipole). The AIPS++ glossary refers to them as antenna/i.f.-gains.

In addition to these `single IF-channel' effects there are two complex leakage terms, D_p, D_q, which describe the polarization mixing that occurs. Given two ideal, orthogonal polarization signals, E_p, E_q, the measured signals are given by:

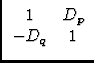
$\displaystyle \left(\vphantom{\begin{array}{cc}E'_p \\ E'_q \end{array}}\right.$ $\displaystyle \begin{array}{cc}E'_p \\ E'_q \end{array}$ $\displaystyle \left.\vphantom{\begin{array}{cc}E'_p \\ E'_q \end{array}}\right)$ = $\displaystyle \left(\vphantom{\begin{array}{cc}1 & D_p\\ -D_q & 1 \end{array}}\right.$ $\displaystyle \begin{array}{cc}1 & D_p\\ -D_q & 1 \end{array}$ $\displaystyle \left.\vphantom{\begin{array}{cc}1 & D_p\\ -D_q & 1 \end{array}}\right)$ $\displaystyle \left(\vphantom{\begin{array}{cc}E_p \\ E_q \end{array}}\right.$ $\displaystyle \begin{array}{cc}E_p \\ E_q \end{array}$ $\displaystyle \left.\vphantom{\begin{array}{cc}E_p \\ E_q \end{array}}\right)$ .

(2)

These leakage terms are assumed to be time independent and constant over the bandpass. Each pair of IF-channels for a particular frequency will have its own leakages however.

Two additional corrections Miriad can perform:

for planet observations Miriad can remove variations in the planet flux and orientation using ephemeris values for apparent size and orientation,
for spectral line observations Miriad can perform Doppler tracking to correct for observatory velocity.

Calibration Schemes

A `standard' ATCA observation consists of a short observation of a primary flux calibrator and a sequence of secondary calibrator and program source observations. In Miriad calibration proceeds as follows:

1.: use primary calibrator to solve for bandpass and complex gains in coupled fashion (assuming zero leakage and unpolarized calibrator),
2.: use primary calibrator (with known polarization) to solve for leakage and complex gains in coupled fashion (applying bandpass),
3.: transfer bandpass and leakage corrections to secondary and use it to derive complex gains (and the Stokes Q, U parameters of the secondary);
4.: alternatively, for a strong secondary with good parallactic angle coverage, determine the bandpass from the secondary followed by the leakage and complex gains (and Stokes Q, U parameters of the secondary),
5.: rescale the gains of the secondary using the known flux of the primary,
6.: transfer all corrections to the program source and image it,
7.: optionally perform selfcal of the complex gains.

The main difference with classic-AIPS calibration is the determination of the Stokes parameters of the secondary in the solution for the complex gains. This is necessary because generally XX and YY are not good estimates of Stokes I (unlike RR, LL) due to linear polarization of the secondary.

The leakage solution cannot solve for all leakage terms using just a primary with known and secondary with unknown polarization. The absolute leakage, or e.g., the X-leakage on the reference antenna, has to be assumed to be zero. Using an observation of a strongly polarized calibrator with known polarization and good parallactic angle coverage these terms can be solved for. The Stokes V parameter also cannot be solved for.

Presently the Miriad bandpass and leakage solvers allow only a point source in the phase center as the model. In AIPS++ we should generalize this to arbitrary models. The bandpass solver allows a frequency dependent model for the source to be specified (to avoid contaminating the bandpass with the spectral index of the calibrator). Similarly, the polarization leakage solver allows a full Stokes model to be specified. Solving for and applying a time dependent bandpass is difficult in Miriad, in AIPS++ we should provide this capability.

There are two selfcal tasks in Miriad, one assumes there is only a single time variable complex gain per antenna, the other allows two gains (X and Y) to be solved for, either independently or phase coupled. There are provisions to specify selfcal models that vary with frequency, polarization or pointing (mosaicing). Not all these options can be combined at present.

We need to be able to cope with several special cases: the data may consist of only a single polarization (XX), two polarizations (XX,YY) or the full set (XX,XY,YX,YY). Only in the last case can we do polarization leakage correction.

One area where Miriad has a rather simplistic approach compared to classic-AIPS is the association of calibration with data. Only a single version of each table (bandpass, leakage, gain) is supported. Recalibration overwrites the old table. There are no provisions for applying the gains from calibrators selectively to some program sources but not others. The solution for these problems in Miriad is to split the data into different sources or groups and apply calibration to these separately. AIPS has a task, CLCAL, which allows one to specify in detail which calibrator to associate with which program sources. Having used both methods, I tend to favor the Miriad approach as the conceptually easier one. In the case with multiple frequencies and multiple 'calibration groups' selectively redoing the calibration can get rather difficult in AIPS. In AIPS++ we might avoid the copy of the actual data when splitting up the observation and provide 'referencing' datasets to which calibration can be applied. Comments on the merits of these schemes are appreciated.

Some effects we might want to consider

Faraday rotation - could be significant at 20cm, may be non-isoplanatic
Bandpass - proper treatment of S/N at band edges, 'effective frequency' for continuum images
Tied array mode, Adding array mode (incoherent)
Interferometer based errors - correlator, time & bandwidth smearing
Off-axis polarization, Asymmetry of primary beam
Redo/undo on-line Tsys calibration
Doppler tracking

Summary of basic requirements

A Solver for bandpass and gain using the parallel hand correlations.
A Solver for polarization leakage, gain and optionally source polarization using all four correlations.
Selfcal Solvers using either single Stokes (I) correlation data or multiple correlations.
A Corrector for each of bandpass, leakage and antenna/i.f.-gain and a versioning scheme for either the Correctors or their underlying tables.

Acknowledgements

Thanks go to Bob Sault and Wim Brouw for their suggestions.