Description
This function enables fitting single component source models
to the uv-data selected by a prior run of setdata. If the
selected data span multiple spectral windows, a single model
will be fit to them jointly.
The function is in the calibrater tool because it is desirable to fit
a resolved calibrator with a resolved component shape after phase
calibration but before amplitude calibration, to improve the
quality of the amplitude calibration solution.
The supported component types are points, elliptical Gaussians, or
elliptical Disks, and their integrated flux density, direction
offset (from the phase center), and (if applicable) their shape
parameters are derived using a non-linear fitting algorithm.
A subset of their parameters may optionally be held fixed.
Use of modelfit is straightforward:
The niter parameter is used to specify how many non-linear
fitting iterations should be used before quitting. Since the adequacy
of the model component choice is not known a priori, modelfit
does not attempt to automatically detect convergence; it will do as
many iterations as specified (not counting iterations which spuriously
increase chi-squared). A few to a few 10s of iterations is usually
adequate. If not, then the requested fit is ill-conditioned.
The type parameter is used to indicate which component type to
solve for. Use "P" for a point, "G" for an elliptical Gaussian,
or "D" for an elliptical disk. modelfit will do its best to
fit the selected shape.
The par parameter is used to specify a starting guess for the
component parameters. Three parameters are required for a point
component: integrated flux density, and RA and Decl direction
offsets (arcsec). Three additional parameters are required for the elliptically
shaped components: the ellipse major axis size (arcsec), the ellipse
axial ratio (< 1), and the major axis position angle (deg, measured
from North thru East on the sky).
The vary parameter is a vector of Bools that indicate which of
the component parameters specified in par should be varied in
the fit. The default is to vary all of the component parameters (all
T). If any elements of vary are set F, the
corresponding parameters in par will be held fixed in the
fitting.
The file parameter is used optionally to specify a table name in
which will be created at the conclusion of the fit to contain the
result component (as a componentlist). This componentlist table
can be used in other applications, e.g., in imager.ft() to
specify a model for filling the MODEL_DATA column for subsequent
processing.
It is generally very important to give a decent ("close enough")
starting guess for the parameters. The way to think about this is
that, for a single point component, all peaks (positive or negative)
in the dirty image correspond to local minima in chi-square, and the
fit can be trapped in any of them. You want the fit to get trapped in
the correct (global) one. This generally means that the first guess
should be within a factor of a few of the correct flux density, within
a (naturally weighted) beamwidth of the correct direction offset, and
a factor of a few of the correct size. The other parameters are
somewhat less sensitive to the starting guess (being limited in range
or cyclical). These estimates of adequacy can be complicated by
correlations between the parameters for some sets of values.
Interactive and autmatic means of providing optimal first guesses are
under consideration for future versions, which will also support
multiple components.
The errors reported by modelfit are robust if the data weights are
strictly inverse variance weights with no arbitrary global scaling and
the model component choice is appropriate. If these conditions hold,
the reduced chi-quared should approach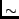 
1, and the parameter
error estimates will be solid formal errors. If the weights are
arbitrarily scaled, so too will be the chi-squared and error
estimates. Interpret these with caution! An excess in the converged
chi-square could indicate either a global mis-scaling of the weights
(hopefully), or that the model component just isn't a good
representation of the source. In either case, the reported errors
will be wrong. If the weights are mis-scaled and the model is,
in fact, a good fit, then the errors will be under-estimated by
approximately the square root of the reduced chi-squared value (which
may be < 1, in which case the errors are actually over-estimated).
Pending improvements:
- Provide interactive (and automatic) means of specifying
components. This will be particularly useful when the source
is not expected to lie at the phase center.
- Fit multiple components. This is mainly limited by the
inadequate means of specifying a priori components. The multiple
component option may be limited to a standalone modelfit application,
to keep the calibrater.modelfit interface simple.
- Improve error estimation and reporting, including access
to the full covariance matrix.
- Permit on-the-fly averaging in frequency and time, to
improve performance.
- Fit for component polarization
- Fit for spectral index for multi-spectral window or
multi-channel data.
- Support more component shapes, e.g., optically thin
ellipsoid, elliptical rings, etc.
Example
mycal:=calibrater('uvmod_test.ms');
# an offset point source
mycal.setdata(msselect='FIELD_ID==4'); # select field 4
mycal.modelfit(niter=10, # 10 fitting iterations
type='P', # fit for a point
par=[1.0,3.0,1.0]); # first guess
# an offset disk
mycal.setdata(msselect='FIELD_ID==6'); # select field 6
mycal.modelfit(niter=15, # 15 fitting iterations
type='D', # fit for disk
par=[3.0,2.5,-2.5,7.0,0.5,0]); # first guess
# a Gaussian at the phase center, for keeps
mycal.setdata(msselect='FIELD_ID==2'); # select field 2
mycal.modelfit(niter=10, # 10 fitting iterations
type='G', # fit for Gaussian
par=[2.0,0,0,1.0,0.5,0], # first guess for pars
vary=[T,F,F,T,T,T] , # fix direction (at phase center)
file='gauss1.cl'); # export a component file
myimgr:=imager('uvmod_test.ms'); # fill resulting model into
myimgr.setdata(fieldid=2); # MODEL_DATA column
myimgr.ft(complist='gauss1.cl');
myimgr.done();
....more calibration steps....
mycal.done();
Next: calibrater.fluxscale - Function
Up: calibrater - Tool
Previous: calibrater.correct - Function
Contents
Index
Please send questions or comments about AIPS++ to aips2-request@nrao.edu.
Copyright © 1995-2000 Associated Universities Inc.,
Washington, D.C.
Return to AIPS++ Home Page
2006-10-15
News