
 News News |
 FAQ FAQ
|
 Search Search
|
 Home Home
|
| Getting Started | Documentation | Glish | Learn More | Programming | Contact Us |

| Version 1.9 Build 1556 |
|
| Package | utility | |
| Module | functionals | |
| Tool | functionalserver |
| minorder | in | the order of the minimum (high-pass) cutoff of the curve | |
| Allowed: | integer | ||
| Default: | 1 | ||
| maxorder | in | the order of the maximum (low-pass) cutoff of the curve | |
| Allowed: | integer | ||
| Default: | 1 | ||
| mincut | in | the characteristic cutoff value of the minimum (high-pass) portion of the curve. | |
| Allowed: | numeric | ||
| Default: | -1.0 | ||
| maxcut | in | the characteristic cutoff value of the maximum (low-pass) portion of the curve. | |
| Allowed: | numeric | ||
| Default: | 1.0 | ||
| center | in | the location of the peak of the bandpass curve | |
| Allowed: | numeric | ||
| Default: | 0.0 | ||
| peak | in | the maximum value of the bandpass curve | |
| Allowed: | numeric | ||
| Default: | 1.0 | ||
In analog electronic filter design, a Butterworth low-pass filter is
one in which the amplitude transfer function,
| H(j![]() )| (where
j =
)| (where
j = ![]() and
and ![]() is the angular frequency), is given by:
is the angular frequency), is given by:
| H(j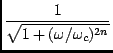
|
(1.13) |
Filter theory provides transformations for deriving transfer functions
of high-pass and band-pass filters which reflect how the electrical
circuits actually work. However, to simplify this class's implementation
and to make the transfer function behavior more predictable by the naive
user, this functional does not actually use the proper transformations.
Instead, the Butterworth bandpass transfer function is approximated by
low pass component, given above, combined with a pseudo high-pass function
that is of the same form but with ![]() substituted with -
substituted with - ![]() .
Both components are shifted such that its peak transfer point is at a
given "center" position.
.
Both components are shifted such that its peak transfer point is at a
given "center" position.
The character of the band edges can be set independently for both ends
of the passband. The cuttoff value-where the signal is attenuated to
1/![]() of the peak-is set with the mincut and
maxcut arguments for the low end (i.e. high-pass) and high
end (i.e. low-pass) portions of the curve, respectively. This value
is the value of
of the peak-is set with the mincut and
maxcut arguments for the low end (i.e. high-pass) and high
end (i.e. low-pass) portions of the curve, respectively. This value
is the value of ![]() for each side of the passband. The order of
the attenuation curve-n in the above formula-can be set using
minorder and maxorder.
for each side of the passband. The order of
the attenuation curve-n in the above formula-can be set using
minorder and maxorder.
- butt := dfs.butterworth(minorder=4, maxorder=4, mincut=10,
maxcut=50, center=30, peak=1)
- butt.state()
[type=10, order=-1, ndim=1, npar=4, params=[30 10 50 1] , masks=[T T T T] ,
mode=[minOrder=4, maxOrder=4]]
- butt.f([0, 7, 10, 13, 30, 47, 50, 53, 60])
[0.193786 0.496351 0.707107 0.886488 1 0.886488 0.707107 0.496351 0.193786]
To plot this function...
- include 'pgplotter.g' - pg := pgplotter() - x := [-30:90] - y := butt.f(x) - pg.plotxy1(x, y, ylab='Bandpass')