Getting Started

Documentation

Glish

Learn More

Programming

Contact Us

Version 1.6 Build 363

News	FAQ
Search	Home

Subsections

• 1.1 Introduction
• 1.2 Calibration philosophy
• 1.3 Practical use of the calibrater tool
• 1.4 References

1. Synthesis calibration

Athol Kemball & George Moellenbrock

1.1 Introduction

This chapter describes how to calibrate synthesis data. At present, this covers data only from connected-element arrays or VLBI data for which fringe-fitting has already been performed elsewhere. The discussion currently covers treatment of calibration effects in the uv-plane; calibration of image-plane effects will be described in a future version of this document.

The major AIPS++ tools that one will need to use are:

Calibrater

is used for applying or solving for a range of uv-plane calibration effects, and plotting of calibration solutions.

Imager

is used for gridding and Fourier transformaton of a MeasurementSet, deconvolution via various methods, and prediction of model visibilities from deconvolved images. Calibration of image-plane effects (those that are a function of direction in the sky) are handled in this tool.

Msplot

is used for plotting and editing of visibility data, and is useful for investigation and editing during calibration cycles.

Componentmodels

are used to represent the sky brightness by discrete components. Such models may be used in imaging and calibration to improve the quality of the results.

In addition, you will need to use the Viewer (see also the Display section of Getting Results) to examine your images, and perhaps the MeasurementSet tool Ms to load and save MeasurementSets.

1.2 Calibration philosophy

As a starting point, it is useful to consider the overall calibration philosophy used in AIPS++. The calibration system has been designed to meet several important goals: i) support for synthesis and single-dish radio-telescopes in a generic formalism which minimizes instrument-specific differences; ii) modeling of all relevant physical effects which may corrupt the observed data, in both the uv- and image-plane, such as propagation or instrumental response factors, in a unified framework; and iii) support for arbitrary parametrization of the individual calibration effects.

1.2.1 The Measurement Equation

All radio-astronomical synthesis data reduction packages have an implicit calibration formalism, which includes a set of calibration effects which may be applied or solved for, and a mathematical framework for how these provide a relationship between the observed and corrected data. Even if this mathematical relationship is not given explicilty, it is, of necessity, enshrined in the infrastructure code.

AIPS++ has explicitly adopted the measurement equation (ME) formalism (Hamaker, Bregman and Sault 1996; Sault, Hamaker and Bregman 1996; Hamaker and Bregman 1996, Hamaker 1998, Noordam 1995; and Cornwel 1995) as the underlying calibration framework. It meets the objectives described in the preceding paragraph, and is easily extended to full coverage of a complete set of image-plane calibration effects (see AIPS++ Note 191). The generic nature of the ME, and its independence on the polarization basis for the data or the calibration parametrization are particularly strong advantages.

A misperception of the measurement equation is that it seeks to describe the physical processes or environment affecting the observed data at a needless or semi-infinite level of detail. This is mistaken; the arbitrary parametrization of the individual calibration effects allows the level of detail to be set at an arbitrary level of coarseness, consistent with available data or even expediency.

It is useful to examine a mathematical representation of the calibration formalism, as it has been adopted. Before describing the measurement equation in this form we need to consider some preliminary definitions for this particular formalism. A generic interferometer is considered to measure a four-vector of cross-correlations $\vec{V}\,$ between two recorded polarizations (p, q) for each of two feeds (i, j) characterizing an individual baseline. This measured vector includes instrumental calibration effects and is denoted by:

$$\vec{V}_{\rm ij}^{} \left(\vphantom{ \begin{array}{c} {V}_{\rm pp}\\ {V}_{\rm pq}\\ {V}_{\rm qp}\\ {V}_{\rm qq} \end{array}}\right. \begin{array}{c} {V}_{\rm pp}\\ {V}_{\rm pq}\\ {V}_{\rm qp}\\ {V}_{\rm qq} \end{array} \left.\vphantom{ \begin{array}{c} {V}_{\rm pp}\\ {V}_{\rm pq}\\ {V}_{\rm qp}\\ {V}_{\rm qq} \end{array}}\right)_{ij}^{}$$ (1.1)

The ME relates the measured vector $\vec{V}\,$ to the true polarized sky brightness, $\vec{\cal I}\,$, which is expressed in a Stokes basis as:

$$\vec{\cal I}\, \left(\vphantom{ \begin{array}{c} I\\ Q\\ U\\ V\\ \end{array}}\right. \begin{array}{c} I\\ Q\\ U\\ V\\ \end{array} \left.\vphantom{ \begin{array}{c} I\\ Q\\ U\\ V\\ \end{array}}\right)$$ (1.2)

Different instrumental and propagation effects are modeled in the ME as calibration components and take the form of four-by-four matrices, acting on four-vectors of the type given above. The calibration components are sub-divided into two general categories based on whether they act in the image- or uv-plane, and they are expressed in the polarization basis (p, q) of the feed, which may typically be circular or linear. Calibration components which are feed-based are constituted as the direct matrix product of separate two-by-two Jones matrices for each feed on the baseline under consideration, as:

$$\left[\vphantom{{{J}_i\otimes{J}^*_j}}\right. \otimes \left.\vphantom{{{J}_i\otimes{J}^*_j}}\right]$$ (1.3)

For a particular calibration component (types listed below), the diagonal elements in the two-by-two Jones matrices describe response to like polarization, and the off-diagonal describe the response to opposite polarization. The direct matrix product of two matrices is defined as:

$$\left(\vphantom{ {\begin{array}{cc} a_{00} & a_{01} \\ a_{10} & a_{11} \\ \end{array}} }\right. \begin{array}{cc} a_{00} & a_{01} \\ a_{10} & a_{11} \\ \end{array} \left.\vphantom{ {\begin{array}{cc} a_{00} & a_{01} \\ a_{10} & a_{11} \\ \end{array}} }\right) \otimes \left(\vphantom{ {\begin{array}{cc} b_{00} & b_{01} \\ b_{10} & b_{11} \\ \end{array}} }\right. \begin{array}{cc} b_{00} & b_{01} \\ b_{10} & b_{11} \\ \end{array} \left.\vphantom{ {\begin{array}{cc} b_{00} & b_{01} \\ b_{10} & b_{11} \\ \end{array}} }\right) \left(\vphantom{ {\begin{array}{cccc} a_{00}b_{00} & a_{00}b_{0... ..._{10} & a_{10}b_{11} & a_{11}b_{10} & a_{11}b_{11} \\ \end{array}} }\right. \begin{array}{cccc} a_{00}b_{00} & a_{00}b_{01} & a_{01}b_{00} &... ... a_{10}b_{10} & a_{10}b_{11} & a_{11}b_{10} & a_{11}b_{11} \\ \end{array} \left.\vphantom{ {\begin{array}{cccc} a_{00}b_{00} & a_{00}b_{0... 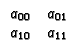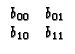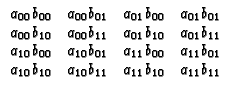..._{10} & a_{10}b_{11} & a_{11}b_{10} & a_{11}b_{11} \\ \end{array}} }\right)$$ (1.4)

The direct product of two Jones matrices thus describes the calibration component's impact on all possible correlation combinations between two feeds.

Provision is also made for multiplicative and additive baseline-based calibration components, which are not decomposed into feed-based terms. These take the form of four-by-four and four-by-one matrices, respectively.

The full ME including image-plane and uv-plane calibration effects can be defined in terms of the quantities described above as:

$$\vec{V}_{ij}^{} \prod \left[\vphantom{{{J^{vis}}_i\otimes{J^{vis}}^*_j}}\right. \otimes \left.\vphantom{{{J^{vis}}_i\otimes{J^{vis}}^*_j}}\right]$$ (1.5)

$$\sum_{k}^{} \prod \left[\vphantom{{{J^{sky}}_i {\left(\underline{\rho}_k\right)} \otimes {J^{sky}}^*_j{\left(\underline{\rho}_k\right)}}}\right. \left(\vphantom{\underline{\rho}_k}\right. \underline{\rho}_{k}^{} \left.\vphantom{\underline{\rho}_k}\right) \otimes \left(\vphantom{\underline{\rho}_k}\right. \underline{\rho}_{k}^{} \left.\vphantom{\underline{\rho}_k}\right) \left.\vphantom{{{J^{sky}}_i {\left(\underline{\rho}_k\right)} \otimes {J^{sky}}^*_j{\left(\underline{\rho}_k\right)}}}\right]$$

$$\vec{\cal I}_{k}^{} \pi \left(\vphantom{{\underline{r}_i-\underline{r}_j}}\right. \underline{r}_{i} \underline{r}_{j} \left.\vphantom{{\underline{r}_i-\underline{r}_j}}\right) \underline{\rho}_{k}$$

where:

• $\left[\vphantom{{{J^{vis}}_i\otimes{J^{vis}}^*_j}}\right.$J^vis_i $\otimes$ J^vis*_j$\left.\vphantom{{{J^{vis}}_i\otimes{J^{vis}}^*_j}}\right]$ and $\left[\vphantom{{{J^{sky}}_i {\left(\underline{\rho}_k\right)} \otimes {J^{sky}}^*_j{\left(\underline{\rho}_k\right)}}}\right.$J^sky_i$\left(\vphantom{\underline{\rho}_k}\right.$$\underline{\rho}_{k}^{}$ $\left.\vphantom{\underline{\rho}_k}\right)$ $\otimes$ J^sky*_j$\left(\vphantom{\underline{\rho}_k}\right.$$\underline{\rho}_{k}^{}$ $\left.\vphantom{\underline{\rho}_k}\right)$$\left.\vphantom{{{J^{sky}}_i {\left(\underline{\rho}_k\right)} \otimes {J^{sky}}^*_j{\left(\underline{\rho}_k\right)}}}\right]$ are individual uv-plane and image-plane calibration components respectively.

• $\underline{\rho}_{k}^{}$ denotes direction, subscript k indexes directions, and ($\underline{r}_{i}^{}$ - $\underline{r}_{j}^{}$) denotes the interferometer baseline vector.

• The four-by-four matrix S converts the sky brightness Stokes polarization basis to the polarization basis used in the interferometer itself.

• M_ij and A_ij denote multiplicative and additive baseline-based instrumental effects respectively.

• $\prod$ and $\sum$ denote product and summation, respectively.

The ME thus reflects the standard Fourier transform relationship between the uv- and image-planes, and allows for generic calibration in both domains. Time and frequency averaging are implicit in the ME form given here, and are assumed to be over ranges shorter than the timescale for variation of any of the terms in the equation.

In the case of fields-of-view narrow enough that the J_i$\left(\vphantom{\underline{\rho}_k}\right.$$\underline{\rho}_{k}^{}$ $\left.\vphantom{\underline{\rho}_k}\right)$ are constant with $\underline{\rho}_{k}^{}$, these terms may be factored out of the summation and treated uv-plane effects J_i, and the measurement equation may be simplified to (ignoring baseline-based effects):

$$\vec{V}_{ij}^{} \prod \left[\vphantom{{{J^{vis}}_i\otimes{J^{vis}}^*_j}}\right. \otimes \left.\vphantom{{{J^{vis}}_i\otimes{J^{vis}}^*_j}}\right] \vec{V}_{ij}^{ideal}$$ (1.6)

$\vec{V}_{ij}^{ideal}$ represents the visibilities measured by an ideal interferometer, and implicitly contains the Fourier transform of the sky.

The individual calibration effects (in either the uv- or image-plane) are denoted by single letter abbreviations, each representing the two-by-two Jones matrix for the ith feed. These include:

G_i

- the composite complex electronic gain of all components located after the feed in the signal path, but excluding the correlator.

T_i

- atmospheric tranmission effects which are independent of polarization (i.e., not including Faraday rotation). Useful for modelling tropospheric gain losses.

F_i

- propagation effects due to Faraday rotation.

D_i

- instrumental polarization response.

E_i$\left(\vphantom{\underline{\rho}_k}\right.$$\underline{\rho}_{k}^{}$ $\left.\vphantom{\underline{\rho}_k}\right)$

- electric field pattern describing the primary beam response, usually normalized with respect to G_i.

B_i

- bandpass response, possibly normalized relative to G_i.

C_i

- feed configuration matrix. This describes the nominal feed configuration, including rotation or conversion of linear to circular polarization. This term is known a priori, and handled implicitly.

P_i

- parallactic angle. This is known analytically.

Since these matrix components may not commute, the order in which they appear in the measurement equation is important. In general, the correct order is given by the order in which the terms affect the incoming wavefront. Thus, a spectral line polarization observation would be described (ignoring primary beam and direction-dependent Faraday rotation) by the measurement equation as (recalling Equation 1.3):

$$\vec{V}_{ij}^{} \vec{V}_{ij}^{ideal}$$ (1.7)

The measurement equation is implemented in AIPS++ by sub-dividing the machinery dealing with image-plane and uv-plane calibration between imager and calibrater respectively. The remainder of this chapter treats the case illustrated in equation 1.7, i.e., uv-plane effects which are handled by the calibrater tool.

1.2.2 Data representation and
the calibration mechanism

AIPS++ stores synthesis uv-data in a MeasurementSet (MS), and it is important to understand how observed and calibrated data are treated in this framework. The observed data are stored in the DATA column in the MAIN MS table; additional columns are added during processing for CORRECTED_DATA and MODEL_DATA. The CORRECTED_DATA column contains the data which result when applying all desired visibility-plane calibration corrections, moving from left to right across the uv-plane portion of the ME. This provides corrected data suitable for imaging.

The MODEL_DATA column, in contrast, is formed by propagating initial source models (perhaps for trial imaging) from right to left through the ME, applying the supported image-plane corrections, and Fourier transforming to the uv-plane. This realizes a best guess for the $\vec{V}_{ij}^{ideal}$ term in equation 1.7. The point at which these two columns meet in the ME allows a residual to be computed and thus an estimate of $\chi^{2}_{}$. The calibration component(s) at the intersection point in the ME are solved for by computing gradients of $\chi^{2}_{}$ with respect to the Jones matrices, and performing a standard non-linear least-squares minimization^1.1.

As an example of the calibration mechanism, we recast equation 1.7 to the implicit form used when solving for D, given an existing solution for G and knowledge of P. We ignore the B calibration component, either because the data is from a continuum observation (only one channel), or because we assume that the bandpass shape is unimportant, at least for this stage of the calibration. Since G and P appear on either side of D in the ME, they are applied to the observed data ( $\vec{V}_{ij}^{}$) and model data ( $\vec{V}_{ij}^{ideal}$) terms, respectively:

$$\vec{V}_{ij}^{} \left(\vphantom{{G}_{ij}^{-1}{G}_{ij}}\right. \left.\vphantom{{G}_{ij}^{-1}{G}_{ij}}\right) \left(\vphantom{{P}_{ij} \vec{V}_{ij}^{ideal}}\right. \vec{V}_{ij}^{ideal} \left.\vphantom{{P}_{ij} \vec{V}_{ij}^{ideal}}\right)$$ (1.8)

$$\vec{V}_{ij}^{} \left(\vphantom{{P}_{ij} \vec{V}_{ij}^{ideal}}\right. \vec{V}_{ij}^{ideal} \left.\vphantom{{P}_{ij} \vec{V}_{ij}^{ideal}}\right)^{-1}_{}$$ (1.9)

$$\left[\vphantom{{{D^{vis}}_i\otimes{D^{vis}}^*_j}}\right. \otimes \left.\vphantom{{{D^{vis}}_i\otimes{D^{vis}}^*_j}}\right] \vec{V}_{ij}^{} \left(\vphantom{{P}_{ij} \vec{V}_{ij}^{ideal}}\right. \vec{V}_{ij}^{ideal} \left.\vphantom{{P}_{ij} \vec{V}_{ij}^{ideal}}\right)^{-1}_{}$$ (1.10)

In equation 1.10, the D calibration is realized as the feed-based (two-by-two) Jones matrices which are solved for in the $\chi^{2}_{}$ minimization. It is straightforward to see how this algebraic manipulation can be extended to any of the calibration components, and the flexible implementation of the calibrater tool is clearly evident.

1.2.3 What are the current calibration
capabilities in AIPS++?

At this time, AIPS++ can solve for a wide range of uv-plane effects, including electronic gain (G_i), mean atmospheric tranmission (T_i), instrumental polarization response (D_i), and the bandpass response (B_i). Parallactic angle effects (P_i), and feed configuration (C_i) corrections are pre-computed. The primary beam voltage and polarization response can be corrected in the image-plane ( E_i$\left(\vphantom{\underline{\rho}_k}\right.$$\underline{\rho}_{k}^{}$ $\left.\vphantom{\underline{\rho}_k}\right)$ D_i$\left(\vphantom{\underline{\rho}_k}\right.$$\underline{\rho}_{k}^{}$ $\left.\vphantom{\underline{\rho}_k}\right)$), but not yet solved for.

Synthesis calibration support is most mature for connected-element observations; fringe-fitting capabilities are currently being developed and added. Both self-calibration and cross-calibration are supported.

Synthesis calibration is under active development in AIPS++ with new features added on a regular basis.

1.3 Practical use of the calibrater tool

1.3.1 Setting up the calibrater tool

A Calibrater tool is initialized by specifying an input MS. This is used throughout subsequent calibration. If another MS is to be calibrated at present, a second tool will be required. Note, however, that the facility to append to existing calibration tables allows individual measurement sets to be processed in sequence and does not require the the input data be concatenated.

To construct a Calibrater tool (for a spectral line polarimetry dataset called polspec.ms):

include 'calibrater.g'               
cal := calibrater('polspec.ms')      # Construct tool

If the dataset has not previously been used in a calibrater or imager tool, this step will form the CORRECTED_DATA, MODEL_DATA, and IMAGING_WEIGHT columns. The CORRECTED_DATA column will be initialized as a duplicate of the (observed) DATA column. The MODEL_DATA column will be initialized with unit total intensity point source visibilities. The IMAGING_WEIGHT column will be initialized with unit weights, and is described in more detail in imager tool documentation.

1.3.2 Initial calibrator models

The Calibrater tool requires an initial visibility estimate in the MODEL_DATA column before visibility-plane solvers can be used. This can be specified via a known external source model, expressed as a set of images and/or a list of component models, which are then transformed to the visibility-plane using the Imager.ft function. This initial model can also be derived by imaging the observed data directly, without calibration, where this is possible. Please consult the general Imaging chapter for instructions on forming images.

Alternatively, if the calibrator source is sufficiently compact, it can be regarded as a point source in the initial calibration iteration, or indeed throughout calibration. Upon initialization, the MODEL_DATA column already contains unit total intensity point source visibilities. If a subset of calibrators are to be used to set the flux density scale for the observation, the models for these should be set to the proper flux density. A facility exists to set standard source flux densities on the Baars or Perley-Taylor scales using the function Imager.setjy in the Imager tool. In this case, if the source is not recognized, it is set to an intial flux density of 1.0 Jy.

include 'imager.g'
imgr:=imager('polspec.ms')
imgr.setjy()                  # Set MODEL_DATA column to point-source models 
                              # (of correct flux density, if recognized):

1.3.3 Uv-data selection

Before using Calibrater to solve for any calibration components, selection can be applied to the MS to restrict the subset of uv-data to be used in the solution. This is specified using the Calibrater.setdata method and the very general msselect query argument as follows:

cal.setdata(msselect='FIELD_ID IN [1,2,3]')  # select data only for calibrators 
                                             # (fields 1, 2, & 3 in this case):

Other selection keywords may be included in the msselect parameter, including ANTENNA1, ANTENNA2, SPECTRAL_WINDOW_ID, etc. These are described fully in the Ms tool documentation. Arbitrary selection may be achieved by combining the selection keywords with the logical && and || operators.

1.3.4 Calibration table conventions

The calibration table definition is available in AIPS++ Note 240. Calibration tables are always cumulative for the specific Jones type they contain. Thus they always refer to the observed DATA column as corrected by Jones matrices of other types. Thus, only one calibration table of each type may be applied to correct the data. Provision for incrementally refining the calibration of a specific Jones type, as in self-calibration, is available.

The calibration tables are not attached to a given MS, but contain references to the MS with which they are associated. Thus they can hold calibration solutions from a collection of different measurement sets, as the capability is provided to append to an existing calibration table. The calibration tables are defined by user-specified text names, which are entirely under user control.

1.3.5 Solving for visibility-plane effects

The Calibrater tool contains all the common capabilities required to solve for the calibration components enumerated above. At the start of a cycle to solve for calibration components, a decision needs to be made as to which known components will be applied, which will be solved for, and which will be ignored. These choices are specified using the Calibrater.setapply and Calibrater.setsolve functions. These functions may be run multiple times to arrange to apply and/or solve for sequences of calibration tables of different types. A particular calibration component type may only be specified once in any sequence of setapply or setsolve executions.

The actual solution is done by the Calibrater.solve function, which takes no further input parameters. The resultant solutions can be examined using a basic capability in Calibrater.plotcal, or further using the Pgplotter or Tablebrowser tools.

To obtain standard G (gain) calibration for selected data, with P (parallactic angle) pre-applied anticipating polarization calibration:

cal.setapply(type='P',t=5.0)                # Calculate & apply P on 5-second timescale
cal.setsolve(type='G',t=300.0, refant=15,   # Solve for G (gain)
             table='polspec.gcal')
cal.solve()                                 # Solve

1.3.6 Establishing the flux density scale

Once an electronic gain solution (G_i) has been performed for all calibrator sources, those secondary sources which were assumed to be of unit flux density can be scaled to a primary flux density scale set by known calibrators included in the run. This is achieved using a utility function Calibrater.fluxscale, which takes as input the electronic gain calibration table, a list of primary and secondary sources, and the name of an optional output electronic gain calibration table. The gain factors in the output table will be scaled correctly once the function has completed. It will also report the estimated point source flux density for the secondary sources, based on the ratio of the mean gain modulus between the primary and secondary calibrators, as is standard practice in cases when this method can be used.

cal.fluxscale(tablein='polspec.gcal',         # Transfer flux density scale from 
              tableout='polspec.fluxscale',   # amplitude calibrator (3C286)
              reference='3C286', 
              transfer=['cal1','cal2'])
#
cal.done()                                    # Destroy calibrater tool

1.3.7 Correcting the observed data

The observed data, which are stored in the DATA column, are corrected by using the Calibrater.setapply function to specify the calibration tables to be used, the interpolation intervals and any selection which is to be applied to the calibration tables as they are read into AIPS++. This function, in conjunction with the selection which can be applied to the MS itself via the Calibrater.setdata, allow cross-calibration. The actual application of the corrections is performed using the Calibrater.correct function, which takes no further parameters. Note that this function must be called explicitly if the corrections are to be applied; this does not occur by default after solving for a set of calibration effects.

To apply the scaled 'G' calibration obtained above:

cal := calibrater('polspec.ms')          # Construct
cal.setdata(msselect='FIELD_ID==4')      # Select data to which calibration will be applied:
#
cal.setapply(type='P', t=5.0)            # arrange to apply P (unnecessary if cal tool not reset)
cal.setapply(type='G', t=0.0,            # arrange to apply G table, solutions from source 1:
             table='polspec.fluxscale',
             select='FIELD_ID==1')
#
cal.correct()                            # apply solutions, writing CORRECTED_DATA column:
cal.done();

Application of solutions from other calibrators to other target sources would be done by setting the selection parameters in Calibrater.setdata and Calibrater.setapply appropriately. Muliple sources may be specified in either selection.

1.3.8 Extending calibration to bandpass, polarization, etc.

In general, it is a fairly simple matter to extend calibration to additional calibration components like bandpass and polarization. In the following examples, we assume that the corrupting effects of G dominate the observed data, and that this calibration component has been solved for first, as described above. This is typical of an observation at the VLA using feeds sensitive to RCP and LCP. For arrays using linear feeds (e.g. ATCA), this assumption may be inappropriate for strongly polarized calibrators (see the chapter for ATCA processing). In any case, the general strategy for treatment of several calibration components is to solve for the dominating effects first, and iterate solutions for components which interact significantly.

Extending the examples given above, instrumental polarization (D) calibration proceeds in manner similar to that for G. In this case, particular attention must be paid to the source polarization model since this is where the leverage for this solution originates. For an unpolarized polarization calibrator, the total intensity (Q = U = V = 0) model used in the G calibration is sufficient. However, if the calibrator is significantly polarized (compared to the expected size of the polarization leakage), then it is important to specify a model for Stokes Q and U. If the calibrator is highly polarized compared to the net polarization leakage (e.g., 3C286 at cm wavelengths observed with the VLA), then the polarization model may be obtained by imaging it without polarization calibration. Consult the Imager documentation for instructions. Once the polarization model image is obtained, the Imager.setjy or Imager.ft function can be used to set the MODEL_DATA column accordingly.

With a polarization model in the MODEL_DATA column, obtaining this calibration is straightforward. Anticipating D calibration, note that the above examples have always included explicit application of the parallactic angle (P) correction^1.2. This rotates the parallactic angle variation out of the terms in the ME that contain the nominal interferometer response, and into the terms containing the leakage response for each polarization combination. Since these corrupting terms, which contain the factors being solved for, vary according to the parallactic angle over the course of the observation, and since it is common practice to solve for a single D calibration component per observation (by setting a long solution interval), it is important to set the preavg parameter in Calibrater.setsolve to a timescale shorter than that for significant variation of the parallactic angle. If preavg is not set appropriately, the data will be averaged over the full range of the solution interval, coherence in the corrupting terms will be lost, and the D calibration solution will be incorrect.

cal:=calibrater('polspec.ms');
#
cal.setdata(msselect='FIELD_ID==1')      # Select polarization calibrator:
#
cal.setapply(type='P',t=5.0)             # Arrange to apply existing calibration 
                                         # before solution is made
cal.setapply(type='G',t=0.0,
             table='polspec.fluxscale')
#
cal.setsolve(type='D', t=86400.0, preavg=60.0,   # Arrange to solve for D
             refant=15, table='polspec.dcal')  
#
cal.solve()                                      # Determine solutions:

Given the G and D calibration tables obtained above, bandpass calibration proceeds as follows:

cal.setdata(msselect='FIELD_ID==1')       # Select data for bandpass calibrator
#
cal.setapply(type='P',t=5.0)              # Arrange to apply existing calibration 
cal.setapply(type='G',t=0.0,              # before solution
             table='polspec.fluxscale')
cal.setapply(type='D',t=0.0,
            table='polspec.dcal')
#
cal.setsolve(type='B', t=86400.0,         # Arrange to solve for B
             refant=15, table='polspec.bcal')  
#
cal.solve()                               # Determine solutions
#
cal.done()

Finally, we wish to apply all calibrations obtained above. The example below treats the case where no detailed selection of solutions and target data is desired. Use msselect in Calibrater.setdata and select in Calibrater.setapply (as needed for the different calibration components) to apply calibration to each target source as desired.

cal.setdata()                    # Select all data:
#
cal.setapply(type='P', t=5.0)    # Arrange to apply all existing calibration
cal.setapply(type='G',t=0.0,
             table='polspec.fluxscale');
cal.setapply(type='D', t=0.0,
             table='polspec.dcal');
cal.setapply(type='B', t=0.0,
             table='polspec.bcal')
#
cal.correct()                    # Write corrected data to CORRECTED_DATA column

1.3.9 Self-calibration

Self-calibration is the process by which calibration components are incrementally improved by alternatly re-imaging and re-solving for the calibration. It depends on the assumption that each succeeding calibration enables generation of an improved image^1.3. The uniform design of the calibrater tool with respect to the different calibration components results in a very flexible means of self-calibrating any and all of the components. One can imagine cases where, for example, the G and D components are each alternately improved along with the image. Depending upon the relative importance of these two components (and any others that may be relevant), the exact sequence of calibration and imaging will vary, but, in principle, the AIPS++ calibrater tool enables the best possible overall calibration for a given dataset.

In practice, self-calibration is achieved exactly as the initial calibrations illustrated above, except that the MODEL_DATA column needs to be filled with the improved model before each round of calibration using the imager.ft function. The calibration tables generated in each round of calibration are always cumulative, i.e., they are always to be applied to the (original) DATA column. At this writing, it is necessary to solve for a particular component in the same way each round, i.e., a phase-only G solution cannot be attempted after the amplitude+phase G cross-calibration. This is because it is impossible to apply and solve for the same component at the same time^1.4

1.4 References

Cornwell, T. J., 1995, AIPS++ Note 183.

Hamaker, J.P., Bregman, J.D., and Sault, R.J., 1996, A&AS, 117, 137.

Hamaker, J.P., and Bregman, J.D., 1996, A&AS, 117, 161.

Hamaker, J.P., 1998, in press.

Noordam, J., 1995, AIPS++ Note 182.

Sault, R.J., Hamaker, J.P., and Bregman, J.D., 1996, A&AS, 117, 149.