
| Version 1.9 Build 1367
|
|


Next: Non-isoplanatic Imaging
Up: No Title
Previous: No Title
Subsections
A mosaic image is produced from interferometer data taken from
several different, adjacent pointings on the celestial sphere.
A single-pointing of data can be treated as a mosaic. One
does not want to force the treatment of all single-pointing data
as mosaics, ie, one does not always want to image the entire
primary beam (PB) or correct for the PB.
The mosaic machinery also allows for combining data from telescopes
with different PB's and different imaging models, an interferometer
and a single dish, for example.
One will need to perform ``bulk'' operations on
data from all pointings from one telescope (ie, calibration).
One will need to perform ``piecemeal'' operations on all data
from a single pointing from a single telescope (ie, gridding/FFTing).
For convenience of ``bulk'' operations, all the data from one
telescope should be stored together in one dataset.
Then the ``piecemeal'' operations could be performed
by selecting out subsets of data. In addition to all
the generic data selection possible with single-pointing
interferometers, one must be able to select on sky pointing position
(a single dish selector) and Telescope.
Something like the YegSet Iterator which would step through
all pointings one at a time would be nice.
It is unclear whether the data from multiple telescopes should
be stored in one dataset or in one dataset for each telescope.
The number of different telescopes used will usually be one or two,
so association of mosaic datasets from different telescopes
by hand will not be too cumbersome.
The final product of the MOSAIC imaging algorithm is a plain old
image. The main difference between a MOSAIC image and an image
produced by CLEAN, say, is that it is inappropriate to apply
a PB to the final MOSAIC image: the parameters OBSRA, OBSDEC, and TELESCOP
are not uniquely specified. While it is unclear how they would be used,
if these parameters are present at all, they should be in arrays attached to the
image indicating ALL pointings of ALL telescopes.
There may or may not be an associated SENSITIVITY image, which is
essentially a generalized primary beam, and can be used to determine
the theoretical thermal noise in each pixel.
The fundamental equation at work in mosaicing is derived by making
a pixel by pixel least square fit to the true sky brightness from a number of
overlapping images weighted by the PB:
Imosaic(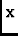 ) = ) = 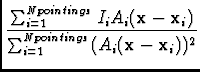
|
(1) |
where
Ii(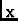 ) is an image made at pointing i, and
Ai(
) is an image made at pointing i, and
Ai(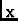 -
- 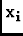 )
is the primary beam of the telescope used for pointing i with
pointing center
)
is the primary beam of the telescope used for pointing i with
pointing center
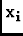 . The square root of the denominator is
the sensitivity image.
. The square root of the denominator is
the sensitivity image.
It has not been specified what kind of
images the
Ii(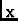 ) are. In some cases, Ii will be independently
deconvolved images. In this case, they may have some permanence
outside the mosaicing method. More common, at least when the MMA
comes on line, will be the case where Ii are dirty images
produced for the sole purpose of making a mosaiced image. The
mosaiced dirty image may then be deconvolved with a single effective
point spread function. In this case, the Ii have no permanence.
And finally, the most complicated case:
) are. In some cases, Ii will be independently
deconvolved images. In this case, they may have some permanence
outside the mosaicing method. More common, at least when the MMA
comes on line, will be the case where Ii are dirty images
produced for the sole purpose of making a mosaiced image. The
mosaiced dirty image may then be deconvolved with a single effective
point spread function. In this case, the Ii have no permanence.
And finally, the most complicated case:
Ii(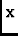 ) = IDi( ) = IDi(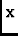 ) - PSFi * (Ai( ) - PSFi * (Ai(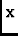 -
- 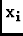 ) )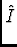 ( (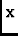 )) ))
|
(2) |
where
IDi(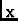 ) is the dirty image made from data from pointing i,
PSFi is the point spread function for pointing i,
and
) is the dirty image made from data from pointing i,
PSFi is the point spread function for pointing i,
and
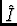 (
(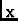 ) is a model image of the entire mosaic field.
An unnormalized mosaic (ie, not divided by the denominator
in Equation 1)
of this quantity is proportional to the gradient of
) is a model image of the entire mosaic field.
An unnormalized mosaic (ie, not divided by the denominator
in Equation 1)
of this quantity is proportional to the gradient of 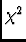 with respect to the model image, and indicates how the model image
must be altered in the next iteration of a maximum entropy mosaicing scheme.
In this case, the
IDi(
with respect to the model image, and indicates how the model image
must be altered in the next iteration of a maximum entropy mosaicing scheme.
In this case, the
IDi(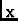 ) and the PSFi (or more conveniently, the
Fourier transform of the PSFi) should persist from iteration to iteration
for efficiency sake, though they could be recreated on each iteration if
memory or disk space were in short supply. The intermediate images
Ii(
) and the PSFi (or more conveniently, the
Fourier transform of the PSFi) should persist from iteration to iteration
for efficiency sake, though they could be recreated on each iteration if
memory or disk space were in short supply. The intermediate images
Ii(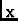 ) can disappear as soon as they are accumulated into the
gradient mosaic.
The IDi and PSFi do not need to persist after the final mosaic
image is formed. While it may be convenient to place each of the IDi
and PSFi into collections of images, they are not really images
of images. The details of how each of the Ii are combined should be
implicit in the coordinate headers of the Ii and the coordinate
header of some template image (ie, the final mosaic image or the gradient
image).
) can disappear as soon as they are accumulated into the
gradient mosaic.
The IDi and PSFi do not need to persist after the final mosaic
image is formed. While it may be convenient to place each of the IDi
and PSFi into collections of images, they are not really images
of images. The details of how each of the Ii are combined should be
implicit in the coordinate headers of the Ii and the coordinate
header of some template image (ie, the final mosaic image or the gradient
image).
The following two ImagingModels require knowledge of some parameters
which seem to reside in the TelModel. The extent of the dependence
of the ImagingModel on the TelModel is analyzed for the case of
varying antenna voltage patterns and varying antenna pointing position.
If the primary beams are different for each antenna,
then a single visibility is related to the sky brightness
distribution via a Fourier sum:
Vj, k(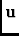 ) = ) = 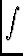 I( I(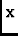 )Ej( )Ej(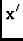 -
- 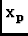 )E * k( )E * k(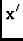 -
- 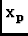 )e-i2 )e-i2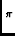 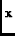 . . 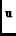 d d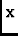
|
(3) |
where
Ej(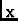 ) is the complex voltage pattern
for the j antenna (
PB(x) = | E(x)|2), and
) is the complex voltage pattern
for the j antenna (
PB(x) = | E(x)|2), and
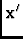 is related
to
is related
to 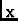 by rotation for azimuth-elevation mount antennas.
For the general case of
Ej
by rotation for azimuth-elevation mount antennas.
For the general case of
Ej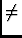 Ek for j
Ek for j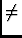 k, it is more
efficient to use a direct Fourier sum than an FFT to calculate a model
visibility from a model sky brightness distribution since the calculation
must be performed one visibility point at a time.
Correction for different voltage
patterns may be important for high dynamic range MMA mosaic
observations. The voltage patterns would probably be determined
holographically. An imaging algorithm would then adjust the image
iteratively using a gradient of
k, it is more
efficient to use a direct Fourier sum than an FFT to calculate a model
visibility from a model sky brightness distribution since the calculation
must be performed one visibility point at a time.
Correction for different voltage
patterns may be important for high dynamic range MMA mosaic
observations. The voltage patterns would probably be determined
holographically. An imaging algorithm would then adjust the image
iteratively using a gradient of 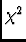 with respect to
I(
with respect to
I(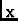 )
which looks something like
)
which looks something like
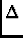 I( I(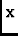 ) = 2 ) = 2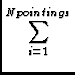 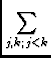 FT(Vi;j, k - FT(Vi;j, k - 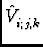 )Ej( )Ej(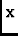 -
- 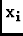 )Ek( )Ek(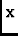 -
- 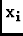 ) )
|
(4) |
where
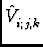 is the model visibility calculated from
the current model of the sky brightness distribution as per
Equation 3.
The basic requirement from Equations 3 and 4
is that the ImagingModel must have access to the complex voltage patterns
for each antenna. Actually, ``VoltagePattern.Apply'' is
the only method required external to ImagingModel.
Under the current understanding, the
voltage patterns would reside in the TelModel. If this is so,
then the VPMosImagingModel requires very little of the TelModel.
is the model visibility calculated from
the current model of the sky brightness distribution as per
Equation 3.
The basic requirement from Equations 3 and 4
is that the ImagingModel must have access to the complex voltage patterns
for each antenna. Actually, ``VoltagePattern.Apply'' is
the only method required external to ImagingModel.
Under the current understanding, the
voltage patterns would reside in the TelModel. If this is so,
then the VPMosImagingModel requires very little of the TelModel.
Pointing errors are thematically similar to different voltage patterns.
A single visibility is related to the true sky brightness distribution
as
Vj, k(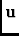 ) = ) = 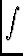 I( I(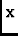 )E( )E(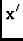 -
- 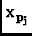 )E * ( )E * (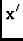 -
- 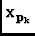 )e-i2 )e-i2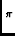 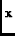 . . 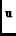 d d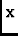 , ,
|
(5) |
where the differences between Equation 5 and
Equation 3
are the inclusion of antenna-dependent pointing positions
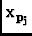 and the omission of antenna dependent voltage patterns. Like the voltage
pattern case, a direct Fourier sum must be used. The equation for the
gradient image will be omitted to save on indices, but the basic idea
is the same as for the antenna-dependent voltage pattern case.
The PEMosImagingModel must have access to a method which supplies
either a pointing correction or an absolute pointing position for
a given antenna and at a given time. Again, this seems to require
that the PEMosImagingModel have knowledge of the TelModel.
and the omission of antenna dependent voltage patterns. Like the voltage
pattern case, a direct Fourier sum must be used. The equation for the
gradient image will be omitted to save on indices, but the basic idea
is the same as for the antenna-dependent voltage pattern case.
The PEMosImagingModel must have access to a method which supplies
either a pointing correction or an absolute pointing position for
a given antenna and at a given time. Again, this seems to require
that the PEMosImagingModel have knowledge of the TelModel.
It is unclear whether these imaging methods for these two
pathological cases will actually be implemented. However,
it is known that simulations of pointing errors and
voltage pattern errors (as caused by surface errors, for example)
is required for the design of the MMA and other high frequency
instruments.


Next: Non-isoplanatic Imaging
Up: No Title
Previous: No Title
Please send questions or comments about AIPS++ to aips2-request@nrao.edu.
Copyright © 1995-2000 Associated Universities Inc.,
Washington, D.C.
Return to AIPS++ Home Page
2006-03-28

 News
News  FAQ
FAQ
 Search
Search
 Home
Home

![]() ) are. In some cases, Ii will be independently
deconvolved images. In this case, they may have some permanence
outside the mosaicing method. More common, at least when the MMA
comes on line, will be the case where Ii are dirty images
produced for the sole purpose of making a mosaiced image. The
mosaiced dirty image may then be deconvolved with a single effective
point spread function. In this case, the Ii have no permanence.
And finally, the most complicated case:
) are. In some cases, Ii will be independently
deconvolved images. In this case, they may have some permanence
outside the mosaicing method. More common, at least when the MMA
comes on line, will be the case where Ii are dirty images
produced for the sole purpose of making a mosaiced image. The
mosaiced dirty image may then be deconvolved with a single effective
point spread function. In this case, the Ii have no permanence.
And finally, the most complicated case: