- Determination of image coordinates. For example, ``If the peak emission
is at pixel coordinate
(35.74, 129.05, 11.10), what are the corresponding
image coordinates?''
Answer:
(150.33956, - 35.49803, 847.0145, 8.5729 x 10-4), note
more image than pixel coordinate elements.
- Description of image coordinates - their type, and units. For example,
``How do I interpret the image coordinates returned in the above example?''
Answer: ecliptic longitude (degrees), ecliptic latitude (degrees),
heliocentric velocity (km/s), and LSR velocity (pc/yr).
In this example where the latter pair of coordinates are dependent, a
mechanism will be required to indicate which of them is to be considered
``independent''. Alternatively, in cases like that of (l, m, n) direction
cosines where one of the triple is dependent on the other two
(
l2 + m2 + n2 = 1), it may be more convenient to indicate which of
them is to be considered ``dependent''.
Queries could also be of the form, ``Which axes of my 7-dimensional image
correspond to right ascension and declination?'', or more generally,
``Which axes of my 7-dimensional image correspond to the sky plane?''.
- Determination of pixel coordinates from image coordinates. For example,
plotting the positions of a list of sources on a map.
- Plotting of coordinate grids. This is an extension of determining pixel
coordinates but may also involve using the mapping function in a different
way. For example, to determine the point where a grid line of constant
galactic latitude intersects the frame defined as a line (or in general a
surface) where one of the pixel coordinate elements is constant. The point
of intersection is defined by a mix of image and pixel coordinate elements.
- Transformation of coordinates. For example, the mapping function for a
spectral-line cube which returns right ascension, declination, and
frequency could be modified so that it returns galactic longitude,
galactic latitude, and barycentric velocity. Precession of equatorial
coordinates is another example, as is changing the units of the returned
coordinate elements (e.g. degrees
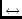radians, kilometers
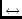miles).
- General linear transformations. For example, translating, scaling, or
rotating the coordinate axes (as opposed to regridding the pixels).
- Interpolation of an image onto a new grid so that its coordinate system
transforms to a specified coordinate system, in particular, that of
another image. This will be required to overlay images with different
coordinate systems.
- Extraction of an interpolated ``flat'' n-dimensional subimage of arbitrary
orientation from an m-dimensional image, for example, an oblique 2-D
plane from a 3-D data cube. Although interpolation would be outside the
function of the coordinate system class itself, it must be able to handle
the new coordinate system created by this operation. The extraction of a
single interpolated pixel value may be considered a special case of this
requirement.
This example shows how degenerate mapping functions may arise, since the
association of each pixel in the oblique n-dimensional subimage with its
m-dimensional image coordinate may need to be preserved.
- Extraction of a ``curved'' n-dimensional subimage from an m-dimensional
image. Since a curved surface cannot, in general, be ``flattened'' out
without distortion, it will be necessary to take the m-dimensional
subimage which just contains the surface and define the curved surface as
a subset of this (via a function or lookup table).
There are, however, some notable special cases. For instance a curved
1-dimensional subimage can always be ``straightened out'' and stored in a
1-dimensional vector. Likewise, a corrugated 2-dimensional subimage can
be flattened into a 2-dimensional array. However, since the coordinates
in these instances would almost certainly have to be stored in a look-up
table, it may be preferable to preserve the embedding m-dimensional
subimage even here.
- FITS input and output must be supported.
- Ancillary functions should be provided for reading and reporting
coordinate values in the required form and precision. For example,
formatting angles in DD:MM:SS.S format to the required number of decimal
places, or, as for a right ascension, in HH:MM:SS.SSS time format, or as
a decimal hour, or decimal degrees. Negative angles with a degree field
of zero must be handled correctly, for example
-00o05'27".554.
Dates and times should be reported in the standard AIPS++ date format.
It should be possible to report coordinates in the units specified. For
example, a coordinate element returned by the mapping function in light
years could be reported in parsec. This includes controlling the metric
prefix (where relevant), for example, m (meters) or km (kilometers), pc
(parsec) or Mpc (Megaparsec).
Sufficient information should be stored with the image coordinates to
allow sensible default formatting.
News 
