Version 1.9 Build 1556

News	FAQ
Search	Home

Up: No Title Previous: Requirements

Subsections

Analysis

The operations described above would not necessarily all be included within a coordinate class, CoordSys, but might be implemented as methods of an image class, Image, which uses CoordSys. For example, the operation of regridding an image to conform with a predefined coordinate system does not belong within CoordSys but would rely heavily on the methods provided by it. In this section we will attempt to further refine our understanding of what the CoordSys class consists of.

Spherical Coordinate Systems

Coordinate systems which represent the celestial sphere are of special significance in astronomy and provide a good illustration of an important point concerning the coordinate mapping function. Such coordinate systems consist of a spherical coordinate system together with a (spherical) map projection. The two components are separate entities, and there are good reasons to treat them as such.

Although map projections can only be specified mathematically with reference to a spherical coordinate system, they are in fact geometrical entities which exist independently of any coordinate system. This is most clearly seen in the ``projective'' map projections which may be defined by purely geometrical constructs. The particular spherical coordinate system chosen when representing them mathematically has no special significance, since the projection could be reformulated in terms of any other spherical coordinate system.

Practically speaking, changing an image's map projection, for example changing its obliquity, or changing its type from say orthographic (SIN) to gnomonic (TAN), always requires interpolation on the pixel values and usually changes the shape of objects in the map. On the other hand, transforming an image's coordinate system, for example from equatorial to ecliptic, does not require interpolation and does not distort objects but instead simply introduces a new coordinate grid.

In fact, the dichotomy between the ``static'' and ``transformable'' parts of the mapping function can be seen in other places. For example, the wavelength calibration of an optical spectrum would be the static part of the spectrum's mapping function, whereas expression of the coordinate as a wavelength, frequency, or velocity, or changing its physical units (Å or nm), would be the transformable part. The static part of the mapping function will henceforth be referred to as the coordinate structure function, and the transformable part as the coordinate transformation function.

Distillation of requirements

At a fairly abstract level, AIPS++ coordinate systems must have the following features:

The coordinate system should be definable via the mapping function f (), via its inverse, or both (for processing efficiency). It must be possible to build the coordinate system (i.e. define f () or its inverse) at run time in response to external requests such as FITS input, image manipulation, user activity, etc.
Degenerate mappings such as might correspond to (RA, dec) $\rightarrow$ (l, m, n), and overspecified mappings such as (l, m, n) $\rightarrow$ (RA, dec) must be provided for.
The following functions for transforming coordinates will be needed within CoordSys:
- forward mapping function, f (), which takes $\bf P$ and returns $\bf I$ ,
- inverse mapping function, f^-1(), which takes $\bf I$ and returns $\bf P$ , and
- mixed mapping function, $\varphi$ (), which when given some of the (p₁, p₂,...) and some of the (i₁, i₂,...) returns the others.
Although the mixed mapping function encompasses both the mapping and inverse mapping function, it may well be based upon them.
Transformation of coordinate systems should be done within the CoordSys class. For example, if a mapping function f_e( $\bf P$ ) returns vector $\bf I_{e}^{}$ in equatorial coordinates, it should be possible to tell the CoordSys object to transform f_e() to f_g() which returns vector $\bf I_{g}^{}$ in galactic coordinates.
It will often be required to transform coordinates which exist without reference to any image. For example, transforming a list of source positions in equatorial coordinates to galactic coordinates does not relate to any image, but is intimately related to the coordinate transformation function part of the mapping function. The transformation function should therefore be accessible outside the context of CoordSys for use by Coordinate objects for general coordinate transformations.
Coordinate iterators should be supplied for the Coordinate class.
General linear transformations should be handled within CoordSys. Translations can be handled by adding an extra dimension to the transformation matrix, as is done with the ``CTM'' (current transformation matrix) in POSTSCRIPT.
Subimage coordinate systems, including those of oblique subimages, can be derived from the parent image by transforming the linear transformation matrix which forms a part of the mapping function (see the following example).
Where the dimensionality of a subimage is less than that of its parent image, the CoordSys object of the subimage may have to be derived from the parent but with dimensional restrictions. For example, an oblique line (slice) extracted from a 2-dimensional image has only one axis, but clearly it might be sensible to associate the coordinates of the two axes of the parent image (say right ascension and declination) with each point on the slice axis.
One way to do this would be to copy the parent image's CoordSys object to the subimage, apply a rotation, translation, and scale (to account for the interpolation interval) via the linear transformation matrix so that the oblique slice was mapped into the x-pixel axis of the parent image, and then flag the y-pixel coordinate of the subimage as having a constant value of zero (the restriction).
Changes in the relative order of the subimage axes, i.e. transpositions, could be implemented via transpositions of the rows and columns of the transformation matrix.
Since it knows all about the image coordinate system, the CoordSys class should respond to queries concerning the coordinate axis types and their units.
FITS output should be supported on a best effort basis. CoordSys will need a method which can determine whether the mapping function is simple enough to be cast into FITS header form and if so return the associated header cards.
If the coordinate system is too complex for the FITS coordinate model, the AIPS++ FITS writer will have to resort to using random parameters.
Processing efficiency considerations: although the CoordSys class will be involved in some difficult numerical computations it is unlikely that these will be so numerous as to cause a processing bottleneck in themselves.
However, certain mathematical transformations such as FFTs and DFTs are based implicitly on linear coordinate systems and are most efficiently expressed in terms of the coefficients of these linear systems (reference pixel, reference value, and increment for each axis). The alternative of computing the coordinates of each pixel within the inner processing loop of these algorithms is far too inefficient.
Therefore, the CoordSys class must be prepared to supply the coefficients of these linear coordinate systems if it is sensible to do so (this is closely related to the task of producing FITS headers).

Storage coordinates

The relationship between pixel coordinates and the actual storage location of the pixels was not discussed in the above analysis which concerned itself only with the relationship between pixel and image coordinates. Put another way, no assumption has been made concerning the value of the pixel coordinate of the first pixel in the image (top-, or bottom-left hand corner, depending on which is adopted for AIPS++).

It may be useful for the Image class to differentiate between pixel coordinates and storage coordinates which are related to the way pixels are stored and so are inherently integral. For example, the first pixel in an image would always have storage coordinates (1, 1,...). Pixel coordinates might be translated and possibly inverted with respect to storage coordinates.

Some examples of why it may be useful to distinguish between pixel and storage coordinates are:

Where an image was composed of a mosaic of subimages it would be easy to define coordinate systems for all subimages by setting their pixel coordinates to correspond to the pixel coordinates of the larger canvas and copying the CoordSys object for each of them from the canvas (or pointing them to it).
Conversely, testing for equality of coordinate systems of two images (perhaps non-overlapping elements of a mosaic) would revert to testing for equality of their CoordSys objects.
Constructing the coordinate system for a non-oblique subimage would be as easy as resetting the offsets between storage and pixel coordinates and copying the CoordSys object from the parent image.
Translated coordinate systems often arise in image display, especially where panning, scrolling, or split-screen is involved. In this case storage coordinates might correspond to TV pixel coordinates.

Storage coordinates are outside the scope of the CoordSys class which deals only with the relationship between pixel and image coordinates, and it would be the responsibility of the Image class to implement them. This would entail the maintenance of the integral offsets between pixel coordinates and storage coordinates, plus a query function to report the pixel coordinates at each corner of the image. Applications programmers would need to bear in mind that the pixel coordinates of an image don't necessarily begin at (1, 1,...), and with each request for the pixel values from a region of the image they would be supplied with the corresponding pixel coordinates. To save confusion, storage coordinates should only appear in low-level Image methods (possibly as private data) and remain invisible to applications programmers.

Object model

A Rumbaugh object model diagram for the AIPS++ coordinate classes is presented in fig 1. The mapping function, which forms the heart of the diagram, is divided into an ordered sequence of three components, a linear transformation, followed by the coordinate structure function, and then the coordinate transformation function. The subimaging association is modelled as the linear transformation class, and likewise the coordinate transformation association is modelled as the coordinate transformation function class. The relation ``mapping function transforms pixel coordinate to image coordinate'' is represented as a ternary association between these three classes. Also of note, the association between CoordSys and Image is one-to-many to allow for a CoordSys object to be shared amongst more than one Image object, for example, a dirty map, dirty beam, and cleaned maps.

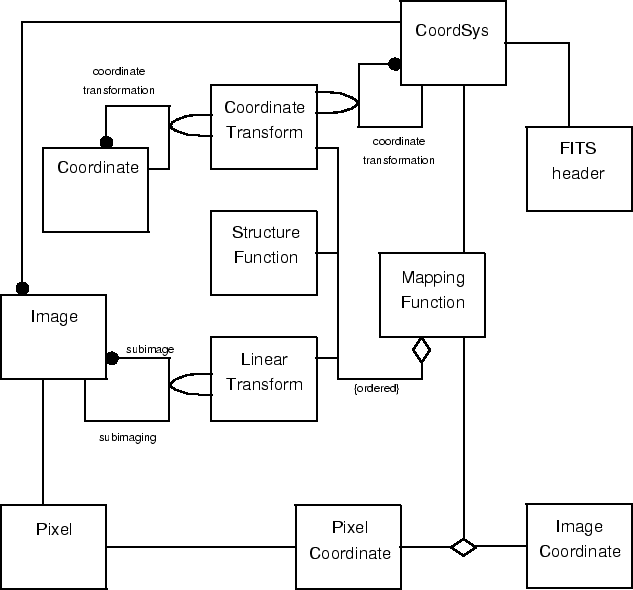
$\epsffile{CoordSysOM.eps}$

Figure 1: Rumbaugh object model diagram for the AIPS++ coordinate classes.

Dynamic model

The dynamic model for the AIPS++ coordinate classes is trivial since they implement a non-interactive computation (the mapping function).

Functional model

A Rumbaugh functional model diagram for the AIPS++ coordinate classes is presented in fig 2. It provides a coarse-grained description of the operation of the mapping function, and shows the operation of each of its three components.

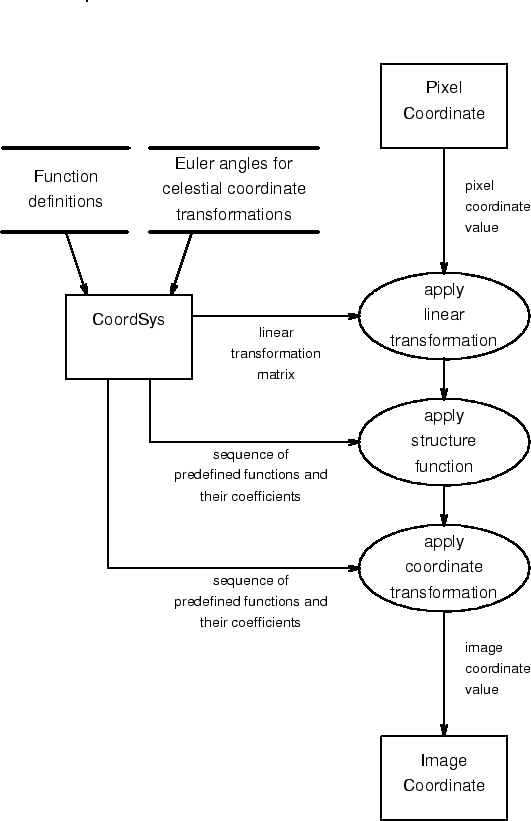
$\epsffile{CoordSysFM.eps}$

Figure 2: Rumbaugh functional model diagram for the AIPS++ coordinate classes.

Data dictionary

Terms used in this document are listed here in glossary form.

Coordinate system - an association between a set of points and a set of tuples of numbers.
Coordinate structure function - the static part of the mapping function representing the physical distortion of an image, for example a spherical map projection or spectral wavelength calibration. It can only be changed by interpolating the image onto a new grid.
Coordinate transformation - a change in the association between the set of points and the set of tuples of numbers which comprise a coordinate system.
Coordinate transformation function - the transformable part of the mapping function. It implements a coordinate transformation.
CoordSys - class of objects containing information which completely describes image coordinate systems, including the axis types (frequency, right ascension, etc.), their physical units (MHz, radians, etc.), and the algorithm for transforming between pixel coordinates and image coordinates.
Image coordinate - a tuple of real numbers which defines a point in a coordinate system associated with an image. The image coordinate system usually represents measurable physical parameters such as time, distance, and angle, and the coordinate elements are the measured valued of these parameters with associated units.
Inverse mapping function - see Mapping function.
Linear transformation - any operation which can be represented by a matrix with constant elements. This includes translation, scaling, rotation, and axis skew. The mapping function incorporates a linear transformation matrix which, in particular, may be used to define the coordinate system of a subimage in terms of its parent image.
Mapping function - the algorithm used to transform pixel coordinates to image coordinates. The inverse mapping function transforms image coordinates to pixel coordinates, and the mixed mapping function is a hybrid of the two.
Mixed mapping function - see Mapping function.
Pixel coordinate - a tuple of real numbers which locates a pixel in an image. The pixel coordinate elements of a pixel are integral, and fractional coordinate elements span the interval between pixels. Pixel coordinates may have an integral offset from storage coordinates.
Storage coordinate - a tuple of integers which locates a pixel in an image. The first pixel in an image has storage coordinate (1, 1,...).

Up: No Title Previous: Requirements