
 News News |
 FAQ FAQ
|
 Search Search
|
 Home Home
|
| Getting Started | Documentation | Glish | Learn More | Programming | Contact Us |

| Version 1.9 Build 1367 |
|
Imaging from the measurement equation requires some careful analysis. We have to accept that there is no inverse to the measurement equation. The dirty image is simply one means of estimating the sky brightness from the measurements. It is convenient because it is linear in the measurements. However, giving it special status obscures the underlying simplicity of imaging.
The dirty image is known to be useful in imaging from simple interferometric observations. Here I will shown how to generalize it to this more complicated measurement equation.
We vary the estimate of the sky brightness
![]() to minimize the
function
to minimize the
function ![]() . For this we need to evaluate
. For this we need to evaluate
![]() . Old hands at this sort of stuff will
recognize that it looks like:
. Old hands at this sort of stuff will
recognize that it looks like:
It is still a long way from this to the dirty image. To make a start,
set the initial model to be zero.
![]()
![]() then becomes
then becomes
![]() . We can read the equation from the inside out as:
. We can read the equation from the inside out as:
The presence of all the transposes is a clue that we are still not
quite there. For unitary matrices, the transpose of the complex
conjugate is the inverse, and so we can recognize the correction of
the various effects. However, there remains a normalization problem.
Furthermore, for non-unitary matrices, we have also to correct for the
amplitude of the various matrices. These points are connected to the
fact that the gradient is not a good search direction for a least
squares method. It is better to pre-multiply by the inverse of the
Hessian. Remember that the Hessian has elements:
![]() Since, in general, this is not practicable we make do with
the inverse of the diagonal elements:
Since, in general, this is not practicable we make do with
the inverse of the diagonal elements:
![]() With a bit more heavy lifting, we get that it must be:
With a bit more heavy lifting, we get that it must be:
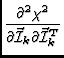 =
= |
2 |
||
| Wij/TD> | |||
| S | (15) |
An appropriate generalization of the dirty image can be defined as the initial update direction for a least squares fit. Applying the Newton-Raphson approach with the approximation that only the diagonal terms are retained, we therefore have that:
Note that the first term on the RHS of this equation is the inverse of a 4 by 4 matrix. By inverting this matrix, we are correcting for the coupling of different polarizations in the interferometer. By ignoring the non-diagonal terms of the Hessian, we are ignoring the coupling between different pixels in the final image. This is reasonable since, first, the coupling is singular, and, second, it is the role of a deconvolution algorithm or Image Solver (see below) to correct for this coupling.
A residual image can be similarly defined as the update direction for
a given estimate of the sky brightness,
![]() .
.
Again, we should check that these equations give the right answers for known, simple cases. Let us consider imaging of Stokes parameter I. The generalized dirty image, as defined in equation 16, is then simply the familiar dirty image:
IDk = 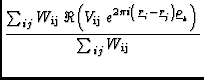
|
(17) |
where I, W and V are now all scalars.
The above-mentioned approximation of dividing by the inverse of the diagonal elements of the Hessian thus corresponds in this case to normalizing by the summed weights, something that is common in constructing a dirty image. This is a good approximation for a point source3 and so the strength of an isolated point source in the generalized dirty image is correctly represented.
Let us turn now to a case for which the full vector formulation is needed: for full polarized observations with gain errors, the generalized dirty image is:
This looks a little more curious and unexpected: the formalism requires that one corrects the gains only on average, not per sample as is usually done, and as arose in the previous section. Furthermore, the correction for the coupling between the different polarization channels is performed by a matrix inversion and multiplication in the image plane. A little thought tells one that this is actually the correct prescription so, as Jan Noordam says in his memo, our calibration procedures do benefit from some careful scrutiny.
Finally, let us look at the case of primary beam correction, and its big brother, mosaicing. Here the vector formulation yields:
Thus again, the primary beam division is done only on average. However, unlike the case of gain errors, this result is somewhat familiar from mosaicing theory (see e.g. Cornwell, Holdaway, and Uson, 1993), except that it is a vector formulation. In this case, one has a linear method that corrects for an image plane effect in an intuitive way.
In summary, I have shown that the GI measurement equation can be used to define a generalized Dirty Image that seems to be quite useful in representing the sky brightness at some level of approximation. Note that the so-called image plane effects, the primary beam, the parallactic angle and the atmospheric phase effects, can be corrected without going through a full non-linear deconvolution. Another way of understanding this evidently unexpected result is that the dirty image is best viewed as the result of one form of deconvolution, special only in its linearity. This same point is made in my memo on the A-matrix formalism (Cornwell, 1992a) but is presented more explicitly here.