
 News News |
 FAQ FAQ
|
 Search Search
|
 Home Home
|
| Getting Started | Documentation | Glish | Learn More | Programming | Contact Us |

| Version 1.9 Build 1556 |
|
A consistent nomenclature and precise definitions are extremely important for a software package like AIPS++, which aspires to be a `world reduction package', and to which workers with a large spacetime separation are supposed to contribute. One of the most sensitive areas in this respect is the Measurement Equation, which underlies the central subject of uv-calibration and imaging.
However, it is not easy to define, adopt and enforce
the use of a suitable set of conventions. This appendix is a hopefully
useful step in that process. It proposes coordinate conventions and
some definitions (notably the one for feed!), and lists symbols
that have been defined in a separate TeX file (referred to as
\include(megi-symbols) in this LaTeX document). The TeX syntax
is shown in small print (e.g. \FeedI), for easy reference.
The following definitions are displayed in a distinctive font throughout the text of this document in order to emphasize that they have been defined explicitly.
\Receptor) converts the incident
electric field into a voltage.
\IFchannel) is one of the two output
signals of a feed, one for each `polarisation'.
NB: The signals in a pair of IF-channels may be a linear combination of
the signals of the two receptors.
\Feed) is the most fundamental
concept of the M.E. formalism, since Jones-matrices are feed-based.
Although a feed may sometimes have only one receptor, it usually
has two, which is necessary and sufficient to fully sample the
incident e.m. field. Each feed is modelled by its own Jones matrix.
NB: A feed is a logical concept. Thus, the same physical
feed may be involved in several logical feeds, e.g. for different
beams in a multi-beam instrument, or for different spectral windows.
\Antenna) is a physical grouping
of feeds. NB: As a concept, it tends to play a rather confusing
role in the M.E. discussions.
\Interferometer) is the
combination of two feeds. Its output is a visibility of 1-4
spectra, depending on the number of IF-channels per feed.
NB: Sometimes the combination of two individual IF-channels is
also called an interferometer. In that case, its output is a single
spectrum.
\Telescope) is an entire
instrument. It can be a single dish (e.g. GBT) or an aperture
synthesis array (e.g. ATCA).
\Projected) angle is an angle
projected on the plane perpendicular to the propagation direction (the
,
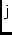
\FeedI,\FeedJfeed labels
,
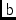
\RcpA,\RcpBreceptor labels, two per feed.
,
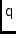
\IFP,\IFQIF-channel labels,two per feed.
,
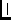
\RPol,\LPolcircular polarisation (right, left)
,
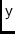
\XPol,\YPollinear polarisation (N-S, E-W)
A+, A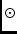
A\ssLin,A\ssCirsuperscripts for linear and circular polarisation
A, A
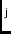
A\ssI,A\ssIJfeed subscripts
The subscript convention of matrix elements is as follows:
![]() refers to a matrix element of matrix
refers to a matrix element of matrix ![]() for feed
for feed ![]() ,
which models the coupling of the signal going from receptor
,
which models the coupling of the signal going from receptor ![]() to IF-channel
to IF-channel ![]() .
.
Fig 1 gives an overview of the coordinate system(s)
used. All angles on the Sky are measured counter-clockwise, i.e. in
the direction North through East. When relevant, `axis' means
`positive axis' (e.g. the positive ![]() -axis). It is important to
make a distinction between:
-axis). It is important to
make a distinction between:
The beam frame(s): In order to calculate the effects of the
primary beam on the signal of a source in direction
![]() (
(![]() ,
,![]() ), the shape and position of the voltage beams
of each receptor on the Sky has to be calculated. For fully
steerable parabolic antennas, which have constant beamshapes, this
can be done most conveniently in coordinate frames defined by the
projected position angles of the receptors. To allow for the fact
that the two beams of a feed are closely coupled, an intermediate
feed-frame is defined also.
), the shape and position of the voltage beams
of each receptor on the Sky has to be calculated. For fully
steerable parabolic antennas, which have constant beamshapes, this
can be done most conveniently in coordinate frames defined by the
projected position angles of the receptors. To allow for the fact
that the two beams of a feed are closely coupled, an intermediate
feed-frame is defined also.
The electrical frame: For the polarisation of the signal, the
only relevant parameters are the projected angles w.r.t. the
`electrical' axes ![]() and
and ![]() defined by the IAU.
defined by the IAU.
NB: In order to see that two frames are needed, consider that Faraday rotation rotates the electric vector, but not the beam on the sky.
Frame of the entire telescope (single dish or array):
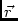
\vvAntPosProjected feed (receptor?) position vector
,
,
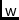
\ccU,\ccV,\ccWProjected baseline coordinates
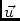
\vvUVWProjected baseline vector(
,
,
)
Electrical frame on the sky (IAU definition):
,
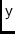
\ccX,\ccYIAU electrical frame on the sky.
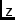
\ccZpropagation direction of incident field.
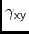
\aaXYAngle from-axis to
-axis (=
/2)
,
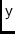
\ccXPol,\ccYPollinear polarisation coordinates.
,
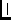
\ccRPol,\ccLPolcircular polarisation coordinates.
Sky frame (w.r.t. fringe stopping centre):
,
,
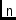
\ccL,\ccM,\ccNCoordinates (direction cosines)
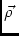
\vvLMNSource direction vector(
,
)
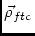
\vvFTCFringe Tracking Centre(RA, DEC,
)
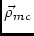
\vvMCMap Centre(
,
)
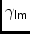
\aaLMAngle from-axis to
-axis (=
/2)
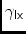
\aaLXAngle from-axis to
-axis (=
/2)
Coordinate frame of feed, projected on the sky:
,
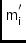
\ccLI,\ccMICoordinates
,
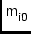
\ccLIO,\ccMIOOrigin (,
) of feed-frame.
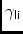
\aaLIAngle from-axis to
-axis
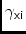
\aaXIAngle from-axis to
-axis ( = -
+
)
Coordinate frame of receptorof feed
, projected on the sky:
,
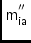
\ccLIA,\ccMIACoordinates
,
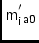
\ccLIAO,\ccMIAOOrigin (,
) of receptor-frame.
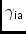
\aaIAAngle from-axis to
-axis
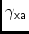
\aaXAAngle from-axis to
-axis ( = -
+
+
)
Coordinate frame of receptorof feed
, projected on the sky:
,
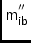
\ccLIB,\ccMIBCoordinates
,
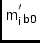
\ccLIBO,\ccMIBOOrigin (,
) of receptor-frame.
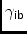
\aaIBAngle from-axis to
-axis
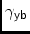
\aaYBAngle from-axis (!) to
-axis ( = -
-
+
+
)
The coordinates
![]() ,
,![]() and
and
![]() ,
,![]() of the frames of
receptors
of the frames of
receptors ![]() and
and ![]() in equ 37 are related
to the celestial coordinate frame
in equ 37 are related
to the celestial coordinate frame
![]() ,
,![]() in a two-step process.
First we define an intermediate feed-frame
in a two-step process.
First we define an intermediate feed-frame
![]() ,
,![]() for
feed
for
feed ![]() , projected on the Sky:
, projected on the Sky:
in which
(![]() ,
,![]() ) is the Pointing Centre of feed
) is the Pointing Centre of feed ![]() , and
, and
![]() (
(![]() ) is a rotation over the projected angle
) is a rotation over the projected angle
![]() between the positive
between the positive ![]() -axis of the Sky frame
and the
-axis of the Sky frame
and the
![]() -axis of the feed-frame.
-axis of the feed-frame.
The voltage beams themselves are best modelled in a receptor-frame
(see equ 37), again projected on the Sky. For
receptor ![]() we have:
we have:
The matrix
![]() (
(![]() ) represents a rotation over the angle
) represents a rotation over the angle
![]() between the positive
between the positive
![]() -axis of the feed-frame and the
-axis of the feed-frame and the
![]() -axis of the relevant receptor-frame.
For receptor
-axis of the relevant receptor-frame.
For receptor ![]() :
:
(![]() ,
,![]() )
and
(
)
and
(![]() ,
,![]() ) represent pointing offsets of receptor
) represent pointing offsets of receptor ![]() and
and ![]() respectively. These can be used to model
`beam-squint' of feeds that are not axially symmetric.
respectively. These can be used to model
`beam-squint' of feeds that are not axially symmetric.
The following matrices and vectors play a role in the Measurement Equation:
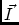
\vvIQUVStokes vector of the source (I,Q,U,V).
,
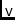
\vvCoh,\vvCohElCoherency vector, and one of its elements.
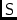
\mmStokesStokes matrix, conversion between polarisation representations.
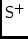
\mmStokes\ssLinConversion to linear representation.
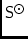
\mmStokes\ssCirConversion to circular representation.
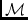
\mmMuellerMueller matrix: Stokes to Stokes through optical `element'
,
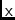
\mmXifr,\mmXifrElCorrelator matrix (4 x 4).
,
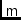
\mmMifr,\mmMifrElMultiplicative interferometer-based gain matrix (4 x 4).
,
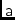
\vvAifr,\vvAifrElAdditive interferometer-based gain vector.
The following feed-based Jones matrices (2 x 2) have a well-defined meaning:
,
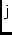
\mjJones,\mjJonesElJones matrix, and one of its elements.
,
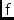
\mjFrot,\mjFrotElFaraday rotation (of the plane of linear pol.)
,
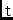
\mjTrop,\mjTropElAtmospheric gain (refraction, extinction).
,
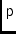
\mjProj,\mjProjElProjected receptor angle(s) w.r.t.,
frame
,
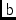
\mjBtot,\mjBtotElTotal feed voltage pattern (i.e.=
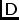
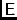
.
,
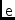
\mjBeam,\mjBeamElTraditional feed voltage beam.
,
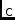
\mjConf,\mjConfElFeed configuration matrix (...).
,
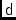
\mjDrcp,\mjDrcpElLeakage between receptorsand
.
,
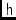
\mjHybr,\mjHybrElHybrid network, to convert to circular pol.
,
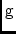
\mjGrec,\mjGrecElfeed-based electronic gain.
,
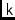
\mjKern,\mjKernElFourier Transform Kernel (baseline phase weight)
,
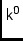
\mjKref,\mjKrefElFT kernel for the fringe-stopping centre.
,
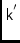
\mjKoff,\mjKoffElFT kernel relative to the fringe-stopping centre.
,
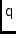
\mjQsum,\mjQsumElElectronic gain of tied-array feed after summing.
Some special matrices and vectors:
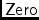
\mmZeroZero matrix
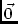
\vvZeroZero vector
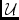
\mmUnitUnit matrix
(a, b)
\mjDiagDiagonal matrix with elements a, b
(a)
\mjMultMultiplication with factor a
(
[,
])
\mjRot[pseudo] Rotation over an angle,
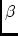
(
[,
])
\mjEllEllipticity angle[s],
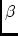
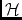
\mjLtoCSignal conversion from linear to circular.
-1
\mjCtoLSignal conversion from circular to linear.
Definitions of some special matrices:
A `pure' rotation
![]() (
(![]() ) is a special case of a `pseudo
rotation'
) is a special case of a `pseudo
rotation'
![]() (
(![]() ,
,![]() ):
):
Ellipticity:
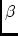
\ppParallParallactic angle, form North pole to zenith
HA\ppHAHour Angle
RA\ppRARight Ascension
DEC\ppDECDeclination
LAT\ppLATLatitude on Earth
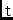
\ccTTime
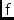
\ccFFrequency
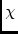
\ppFaradFaraday rotation angle
a\ppAmplAmplitude
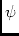
\ppPhasePhase
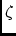
\ppPhaseZeroPhase zero
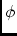
\ppRcpPosDevDipole position angle error
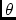
\ppRcpEllDevreceptor ellipticity