
 News News |
 FAQ FAQ
|
 Search Search
|
 Home Home
|
| Getting Started | Documentation | Glish | Learn More | Programming | Contact Us |

| Version 1.9 Build 1556 |
|
Wim Brouw
22 January 1999
A postscript version of this note is available (124kB).
Trying to find a more stable non-linear least squares method (LSQ) than the one currently used in Newstar, I found another few areas that could be added or improved in the existing routines. In the end I produced a set of routines to handle linear and non-linear cases, both with or without SVD, and constraint equations.
In addition the present document describes the usage and background of the different routines.
Least squares solutions in Aips++ have the following general background:
The following terminology is used throughout:
The condition equations can, with the above definitions, be written in one of the following ways:
| ai . x = li i = 0,..., N - 1 | (1) |
or as:
| (2) |
or as:
| C . x = l | (3) |
The normal matrix is defined as:
| A = CT . Q-1 . C | (4) |
| A . x = L | (5) |
For the minimum of ![]() holds:
holds:
|
|
(7) |
which leads to the following set of normal equations:
![$\displaystyle {\frac{\left[ l_{i} - y_{i}\right]}{\sigma_{i}^{2}}}$](img14.gif) |
(8) |
or in matrix form:
or:
| A . x = L | (10) |
| x = A-1 . L | (11) |
After solution for the unknowns
x, ![]() as defined in
(6) can be directly calculated if we rewrite it as:
as defined in
(6) can be directly calculated if we rewrite it as:
![$\displaystyle {\frac{\left[ \left( l_{i}-y_{i}\right)^{2}\right]}{N-n}}$](img24.gif)
|
(14) |
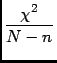
|
(15) |
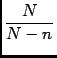
|
(16) |
The uncertainty in the solution xi can be expressed as:
|
|
(17) |
|
xi = |
(18) |
|
|
(19) |
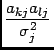
|
(20) |
|
|
(21) |
If the uncertainties in the unknowns are wanted, the inverse matrix A-1 is calculated by backsubstitution of the identity matrix, and the uncertainties by (22).
The merit function we want to minimise in this case is:
Differentiating ![]() leads to the following set of normal equations:
leads to the following set of normal equations:
The normal matrix is Hermitian. It can be solved by Choleski methods.
However, internally the matrix is converted to a real form. Although this has
an, in general, small memory penalty, it has no influence on CPU time, and
makes it possible to use the same routines for complex and real solutions.
The conversion to real is done by splitting each element Aij of the
normal matrix into
A![]() ij +
ij + ![]() A
A![]() ij and replacing it by:
ij and replacing it by:
and simular replacements for the vector elements xi and Li as:
|
xi = |
(26) |
Li = 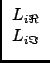
|
(27) |
Another reason for solving real rather than complex equations is given in the next section.
In cases where both the unknowns x and their complex conjugates x* appear in the condition equations, differentiating the merit function (23) will not produce a symmetric or Hermitian normal matrix, since there exists no linear relation between xi and x*i. We could, of course, solve for 2n complex equations with added constraints that the sum of even and odd unknowns must be real, and their difference imaginary, but this will lead to 4n complex equations.
If, however, we consider each complex unknown as two real unknowns (i.e.
xi![]() and
xi
and
xi![]() ) then differentiating (23)
produces the
following symmetric set of 2n real equations:
) then differentiating (23)
produces the
following symmetric set of 2n real equations:
![$\displaystyle \begin{array}{ccccc}
{\left[ {a_{0}}^{*}a_{0}\right]}_{\Re} &
{...
...]}_{\Im} &
\cdots &
{\left[ {a_{2n-1}}^{*}a_{2n-1}\right]}_{\Re}
\end{array}$](img73.gif)
A number of special cases can be distinguished.
In the `normal' complex case (previous section),
a2i ![]() a2i + 1, and
(28) reduces to (25).
a2i + 1, and
(28) reduces to (25).
If all a2i and a2i + 1 are real, but specified, e.g., as a complex number, (28) deteriorates into:
![$\displaystyle \begin{array}{ccccc}
\left[ {a_{0}}_{\Re}{a_{0}}_{\Re}\right] & ...
...ght] & 0 &
\cdots & \left[ {a_{n-1}}_{\Im}{a_{n-1}}_{\Im} \right]
\end{array}$](img83.gif)
Note that in this case there is a true separation of the real and imaginary parts of the different unknowns, and two separate real solutions with each n unknowns will produce exactly the same result.
The full and special cases are all catered for in the aips++ routines.
Using arguments comparable to those in (2.1.1), we can get (13) for the complex case as:
with the a's and x's as defined in (29).
If there are not enough independent condition equations, the normal matrix A cannot be inverted, and a call to WNMLTN will fail with a .false. return value.
The equations could still be solved if some additional `constraint' equations would be introduced. In the more complex cases the precise, let alone the best, form for these additional equations is difficult to determine (e.g. the redundancy situation in Westerbork).
A method known as `Singular value decomposition' (SVD) can be used to obtain the minimal set of orthogonal equations that have to be added to solve the LSQ problem. Several implementations exist in the literature.
In general we can distinguish three types of constrained equations:
The general constraint situation arises from the use of Lagrange multiplicators. Assume that in addition to the condition equations, with measured values, we have a set of p rigorous equations:
We must therefore make|
|
(32) |
|
|
(33) |
Note that I have chosen for having constraint equations linear in the unknowns, with a zero value. In cases where this is not adequate (e.g. x + y + z = 360) a simple linear transformation will suffice to make it e.g. x' + y' + z' = 0.
Defining the second term in (34) as Bik, we can write our expanded set of normal equations as:
The routines to handle this situation use a method based on ``Pseudo-inverse berekening en Cholesky factorisatie'', Hans van der Marel, 27 maart 1990, Faculty of Geodesy, Delft University. I will briefly describe Hans' paper, together with the additions I have made.
In the case we are considering, the normal equation A has not full column rank. Therefore, there exists, if the rank defect is p, an n x p matrix G, a basis for the null-space of A, with AG = 0. If we assume that B has just sufficient constraint equations to solve the rank defect, the inverse of the matrix in (35) is:
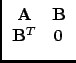
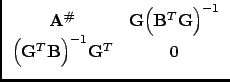
|
(36) |
We can now proceed in the following way:
If n1 = n - n2, we can say that after n1 Choleski steps, we have:
A = 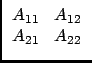
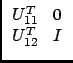
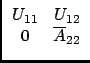
|
(37) |
The collinearity angle ![]() can be determined for the current column i
by:
sin2
can be determined for the current column i
by:
sin2![]() = uii2/aii.
= uii2/aii.
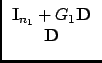
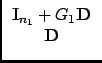
|
(38) |
Errors are determined in the same way as described in (2.1.1), where it should be noted that (13) can either be used summing over n1 variables and using the first guess of x1, or over n and using the final x. Internally the first option is used. The uncertainties in x are determined by calculating the covariance matrix. Using similar arithmetic as in (2.1.1), it can be shown that:
| A-1 = E . a1-1 . ET | (39) |
In the case of known constraints, hence when B is known in (35), this equation can be solved. Cholesky decomposition does not work in this case, and a, transparent, Crout LU decomposition is done to determine the (symmetric) covariance (i.e. inverse) matrix of the left hand side of (35). .
Errors are determined as explained in (2.1.1). Since all
constraint equations are ![]() 0, the sum in (13) is
taken over n, not over n + p if p are the number of constraint equations.
0, the sum in (13) is
taken over n, not over n + p if p are the number of constraint equations.
In the case of non-linear condition equations, no simple solution to minimise
the merit function (e.g. (6)) exists. A simple solution
is to take the condition equation, make a first order Taylor expansion around
an estimated
![]() ; solve for
dx, and iterate till
solution found.
; solve for
dx, and iterate till
solution found.
However, better and more stable methods exist (e.g. steepest-descend) for some circumstances. A method that seems to be quite stable and using both steepest-descent and Taylor expansion, is the method by Levenberg-Marquardt (see e.g. ``Numerical recipes'', W.H. Press et al., Cambridge University Press).
If we have an estimate for x, we can find a better one by:
where H is the Hessian matrix ofThe Hessian matrix H has as elements:
By dropping the second term in (42), and multiplying each Hii term with (1 +| H . dx = b | (43) |
Choosing ![]() is the crux of the matter, and where to stop iterating. A
start value of
is the crux of the matter, and where to stop iterating. A
start value of
![]() = 0.001 is used in the following routines. The method
looks at the
= 0.001 is used in the following routines. The method
looks at the ![]() for
for
![]() + dx. If it has increased
over the value of
+ dx. If it has increased
over the value of ![]() for
for
![]() ,
,
![]() is
unchanged, and
is
unchanged, and
![]() = 10
= 10![]() . If there is a decrease; a new value for
. If there is a decrease; a new value for
![]() is used, and
is used, and
![]() =
= ![]() /10. Iteration can be
stopped if the fractional decrease in
/10. Iteration can be
stopped if the fractional decrease in ![]() is small (say < 0.001);
never if there is an increase in
is small (say < 0.001);
never if there is an increase in ![]() .
.
Errors are calculated as described in (2.1.1). The errors returned by WNMLSN are, of course, only approximations, since the original equations are non-linear, but give a good impression of the residuals. The covariance matrix should be calculated by doing a final linear run on the residuals, and solve the equations.
An LSQ-object takes a total space of:
| 9 | + | (administration) | |
| (n + p)(n + p + 1)/2 | + | (normal array) | |
| 4m | + | (error calculations) | |
| m(m + p) | + | (known sides) | |
| (n + p + 1)/2 | + | (pivot area) | |
| (n + p) | (solution) 8 byte words | (44) |
The following calls are available:
wnb, October 15, 2006