fftserver - Tool

Postscript file available

FFTs and related operations

include "fftserver.g"

Constructors

Construct an fftserver tool

Functions

autocorr	Auto-correlate an array
complexfft	Complex in-place Fourier transform.
convolve	Convolve two arrays.
crosscorr	Cross-correlate two arrays
done	Delete the fftserver tool
mfft	mutiple Fourier transforms.
realtocomplexfft	Real to complex forward Fourier transform.
shift	Shift an array a non-integral number of pixels.

Description

This tool does Fourier transforms and related operations like cross and auto-correlations and frequency domain based shifting. The computation is performed in a pre-compiled executable. It is not interpreted by Glish.

Throughout this module the following definitions will be used for the Fourier transform. A forward transform is one where the exponent is negative and no scaling is done of the result. ie., given a 1-dimensional array, x[t], the Fourier transform, X[f], is given by^1.1:

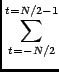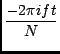X[f] = $\displaystyle \sum_{t=-N/2}^{t=N/2-1}$ x[t]exp( $\displaystyle {\frac{-2\pi i f t}{N}}$ )

A backward transform is one where the exponent is positive and the result is scaled by ${\frac{1}{N}}$ . ie., given a 1-dimensional array, X[f], the Fourier transform, x[t], is given by:

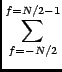x[t] = $\displaystyle {\frac{1}{N}}$ $\displaystyle \sum_{f=-N/2}^{f=N/2-1}$ X[f]exp( $\displaystyle {\frac{2\pi i f t}{N}}$ )

The transforms described above follow the radio-astronomical convention of having the origin of the transform as the centre pixel. This means that if the vector x[t] is symmetric about the centre pixel then the result of a forward transform will also be a real vector. The centre pixel is the one at the (N + 1)/2 location, using integer division, with the first element at index 1.

The length of the Fourier transform is not restricted to a power of two. Any length transform can be done.

Similarly the input data can be an N-dimensional array and N-dimensional transforms will be performed.

Example

To use the functions in this tool we have to firstly (1) load the definition of the fftserver tool and (2) construct a server tool that will actually perform the computations.

  include 'fftserver.g'     # 1
  server := fftserver()     # 2

Step 2 above starts the 'numerics' process if it is not already running.

After creating the server a full complex to complex in-place FFT can be performed:

  server.complexfft(a, 1)     # forward (+1) fft on complex array "a"
  server.complexfft(a, -1)    # reverse (-1) fft on complex array "a"

If you know that you have real-valued arrays, you can perform a real to complex FFT. Here the FFT is not done in place, so the original array is preserved:

  b := server.realtocomplexfft(a)

Note that the output array has the same shape as the input array so that half of the output array is the conjugate of the other half.

FFT-based convolution is available using the convolve function.

  c := server.convolve(a,b)

The input arrays must have the the same number of dimensions, but they do not have to be the same shape, the padding is handled for you. The output array is the size of the larger of the input arrays. These convolutions are ``linear'' ie., the effects of the convolution at one edge do not reflect onto the opposite side of the array.

Auto and cross-correlations of real arrays can also be done.

  c := server.autocorr(a)
  c := server.crosscorr(a,b)

For cross-correlations, the arrays must have the same shape. The correlations are circular, meaning that effects near one edge of the array reflect to the opposite side. If this is not what you want, you should zero-pad the arrays first.

The finally the fftserver tool can do an an FFT-based shift of an array. For example, if a is a 1-dimensional array, then:

  b := server.shift(a, 3.5)

would shift the array 3.5 pixels towards the end of the array. This is equivalent to a band-limited, or sinc interpolation of the array.

Once you have finished doing transforms you can shut down the numerics process, assuming nothing else needs it, using the done function.

  server.done()

See Also
fftserverdemo fftservertest

Next: fftserver - Constructor Up: mathematics - Module Previous: min_with_location - Function Contents Index

	Package	utility
	Module	mathematics