
 News News |
 FAQ FAQ
|
 Search Search
|
 Home Home
|
| Getting Started | Documentation | Glish | Learn More | Programming | Contact Us |

| Version 1.9 Build 1556 |
|
| Package | utility | |
| Module | mathematics |
include "randomnumbers.g"
| randomnumbers | Construct an randomnumbers tool |
| binomial | Generate binomially distributed random numbers |
| discreteuniform | Generate uniformly distributed random integers |
| done | Delete the randomnumbers tool |
| erlang | Generate random numbers that have an Erlang distribution. |
| geometric | Generate geometrically distributed random numbers |
| hypergeometric | Generate random numbers that have an hyper-geometric distribution. |
| lognormal | Generate random numbers with a log-normal distribution |
| negativeexponential | Generate random numbers with a negative-exponential distribution |
| normal | Generate normally distributed random numbers |
| poisson | Generate Poisson distributed random numbers |
| reseed | Set the seed used by the random number generator. |
| type | Return the type of this tool |
| uniform | Generate uniformly distributed random numbers |
| weibull | Generate random numbers with a Weibull distribution |
The randomnumbers tool will generate pseudo-random numbers from a number of common distribution functions.
This tool will generate random numbers from the following distributions:
p(x) = 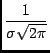 exp exp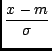
|
(1.14) |
|
p(x) = |
(1.15) |
|
p(x) = |
(1.16) |
|
p(x) = |
(1.17) |
p(x) = 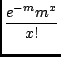
|
(1.18) |
|
p(x) = p |
(1.19) |
p(x) = 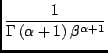 x x |
(1.20) |
|
p(x) = |
(1.21) |
The builtin function random() of glish can be used to generate a sequence of uniformly distributed random numbers. These are random integers between optionally specified bounds. This is a discrete uniform distribution and hence is similar in functionality to the discreteuniform function in this tool.
The C++ class, Random.
The Glish built-in function, random.
include 'randomnumbers.g' #1
rand := randomnumbers(); #2
The rand tool is now ready for use. To generate a sequence of 100 random numbers which are normally distributed with a mean of 0.5 and variance of 1.0 the normal function is used. ie.,
x := rand.normal(0.5, 1.0, 100);
A 10 by 20 two-dimensional array of Poisson distributed random numbers, with a mean of 6.5, can be generated using,
x := rand.poisson(6.5, [10,20]);
The glish variable x would now have a shape of [10,20], where each element of which will be a random number from a poisson distribution.
The random number generator will always produce the same sequence of numbers for a given set of seeds. To generate a new sequence of random numbers, one has to reset the random number generator by supplying a new seed. This can be done using:
rand.reseed(12.34);
where seed can be any number. If called with the unset value, which
is the default, this function will use the glish
random function to supply a seed.
Once you are finished with this tool you should call the done function to release all the memory used by this tool. If no other tools are using the server then this will also be shut down.
rand.done();