
 News News |
 FAQ FAQ
|
 Search Search
|
 Home Home
|
| Getting Started | Documentation | Glish | Learn More | Programming | Contact Us |

| Version 1.9 Build 1556 |
|
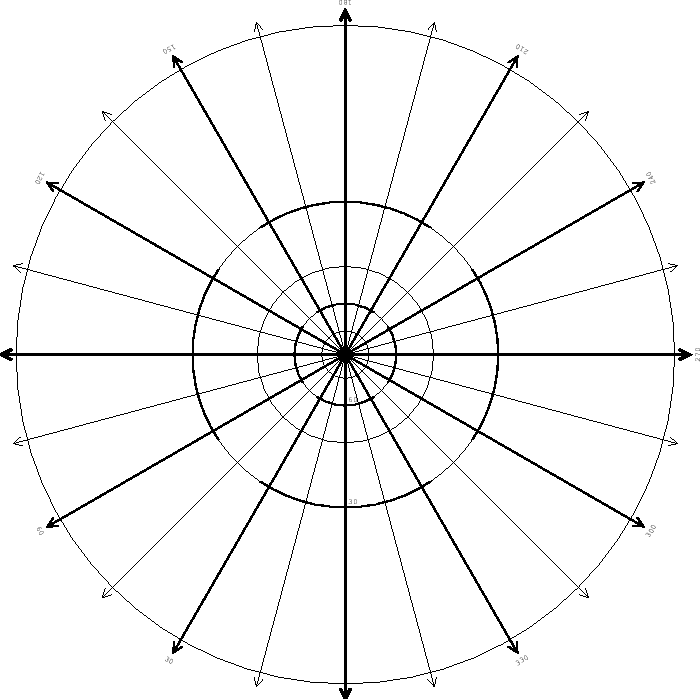
Zenithal projections (also known as azimuthal projections) are a
class of projections in which the surface of projection is a plane. The
native coordinate system is such that the polar axis is orthogonal to the
plane of projection, whence the meridians are projected as equispaced rays
emanating from a central point, and the parallels are mapped as concentric
circles centered on the same point. The projection is therefore defined by
R![]() and A
and A![]() as in the following diagram:
as in the following diagram:
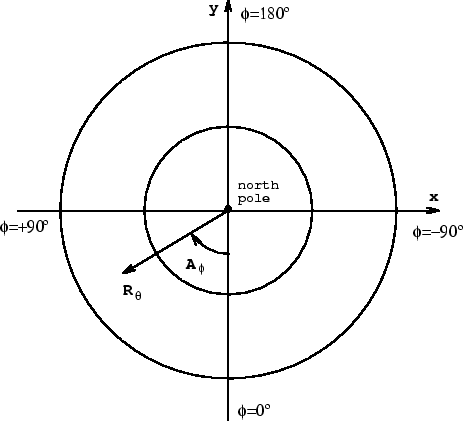
All zenithal projections have
|
A |
(12) |
whence
| x | = | - R |
(13) |
| y | = | - R |
(14) |
These equations may be inverted as follows
| R |
= | (15) | |
| = | arg(- y, - x). | (16) |
Since
|
|
(17) |
the requirement for conformality of zenithal projections is
|
|
(18) |
This differential equation has the general solution
R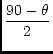
|
(19) |
and this is the form of R![]() for the stereographic projection.
for the stereographic projection.
Let an oblique coordinate system be denoted by
(![]() ,
,![]() ), and let
the coordinates of the pole of the native coordinate system in the oblique
system be
(
), and let
the coordinates of the pole of the native coordinate system in the oblique
system be
(![]() ,
,![]() ). The meridian of the oblique system defined
by
). The meridian of the oblique system defined
by
![]() =
= ![]() will be projected as a straight line segment; suppose it
overlies the native meridian of
will be projected as a straight line segment; suppose it
overlies the native meridian of
![]() =
= ![]() in the same sense of
increasing or decreasing latitude (to distinguish it from the native meridian
on the opposite side of the pole), then the Euler angles for the
transformation from
(
in the same sense of
increasing or decreasing latitude (to distinguish it from the native meridian
on the opposite side of the pole), then the Euler angles for the
transformation from
(![]() ,
,![]() ) to
(
) to
(![]() ,
,![]() ) are
) are
|
( |
(20) |
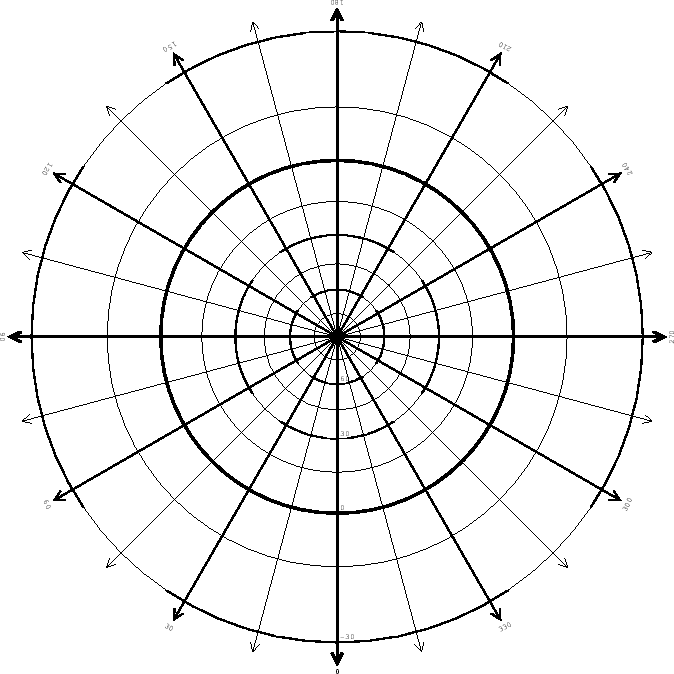
Let r0 be the radius of the generating sphere and let the distance of the
origin of the projection from the centre of the generating sphere be
![]() r0. If the plane of projection intersects the generating sphere at
latitude
r0. If the plane of projection intersects the generating sphere at
latitude ![]() in the native coordinate system of the projection as in
the following diagram
in the native coordinate system of the projection as in
the following diagram
...diagram...
then it is straightforward to show that
R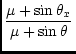
|
(21) |
From this equation it can be seen that the effect of ![]() is to
rescale r0 by
(
is to
rescale r0 by
(![]() + sin
+ sin![]() )/
)/![]() , thereby uniformly scaling the
projection as a whole. Consequently the projections presented in this section
only consider
, thereby uniformly scaling the
projection as a whole. Consequently the projections presented in this section
only consider
![]() = 90o.
= 90o.
The equation for R![]() is invertible as follows:
is invertible as follows:
|
|
(22) |
where
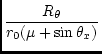 . .
|
(23) |
For
|![]() |
| ![]() 1 the perspective zenithal projections diverge at
latitude
1 the perspective zenithal projections diverge at
latitude
![]() = sin-1(-
= sin-1(- ![]() ), while for |
), while for |![]() | > 1 the projection of
the near and far sides of the generating sphere are superposed, with the
overlap beginning at latitude
| > 1 the projection of
the near and far sides of the generating sphere are superposed, with the
overlap beginning at latitude
![]() = sin-1(- 1/
= sin-1(- 1/![]() ).
).
All perspective zenithal projections are conformal at latitude
(
![]() = 90o). The projection with
= 90o). The projection with ![]() = 1 (stereographic) is
conformal at all points.
= 1 (stereographic) is
conformal at all points.
The perspective zenithal projection with ![]() = 0 is known as the
gnomonic projection. Since the projection is made from the centre of
the generating sphere great circles are projected as straight lines. Thus the
shortest distance between two points on the sphere is represented as a
straight line interval which, however, is not uniformly divided.
= 0 is known as the
gnomonic projection. Since the projection is made from the centre of
the generating sphere great circles are projected as straight lines. Thus the
shortest distance between two points on the sphere is represented as a
straight line interval which, however, is not uniformly divided.
| R |
= | r0cot |
(24) |
| = | tan-1 |
(25) |
Limits: diverges at latitude
![]() = 0o.
= 0o.
Conformal at latitude
![]() = 90o.
= 90o.
The perspective zenithal projection with ![]() = 1 is known as the
stereographic projection. It is conformal at all points and also has
the property that all circles on the generating sphere are projected as
circles. The relative ease of constructing oblique stereographic projections
led to its use by Arab astronomers for constructing astrolabes.
= 1 is known as the
stereographic projection. It is conformal at all points and also has
the property that all circles on the generating sphere are projected as
circles. The relative ease of constructing oblique stereographic projections
led to its use by Arab astronomers for constructing astrolabes.
| R |
= | 2r0tan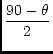
|
(26) |
| = | 90o - 2tan-1 |
(27) |
Limits: diverges at latitude
![]() = - 90o.
= - 90o.
Conformal at all points.
The perspective zenithal projection with
![]() =
= ![]() is known as the
orthographic projection. It gives a representation of the visual
appearance of a sphere (for example a planet) when seen from a great distance.
is known as the
orthographic projection. It gives a representation of the visual
appearance of a sphere (for example a planet) when seen from a great distance.
| R |
= | r0cos |
(28) |
| = | cos-1 |
(29) |

Limits: the front and rear sides of the generating sphere begin to overlap at
latitude
![]() = 0o.
= 0o.
Conformal at latitude
![]() = 90o.
= 90o.
The perspective zenithal projection with
![]() = (
= (![]() /2 - 1)-1 = 1.7519
has approximately equidistant parallels, the length of the meridian from
/2 - 1)-1 = 1.7519
has approximately equidistant parallels, the length of the meridian from
![]() = 90o to
= 90o to
![]() = 0o being true. See also zenithal
equidistant projection.
= 0o being true. See also zenithal
equidistant projection.
The perspective zenithal projection with
![]() =
= ![]() + 1 = 2.4142 is
approximately equal area, the area of the hemisphere being true. See also
zenithal equal area projection.
+ 1 = 2.4142 is
approximately equal area, the area of the hemisphere being true. See also
zenithal equal area projection.
This group contains mathematically defined projections which are designed to have certain useful properties.
The meridians are uniformly divided so as to give uniformly spaced parallels. This projection is useful for mapping the polar regions of a spherical coordinate system when ease of construction and measurement are required.
| R |
= | r0(90 - |
(30) |
| = | 90o - 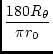 . . |
(31) |
Limits: none.
Conformal at latitude
![]() = + 90o.
= + 90o.
The spacing between parallels is computed to make this an equal area projection.
| R |
= | r0 |
(32) |
| = | sin-1 |
(33) |
Limits: none.
Conformal at latitude
![]() = + 90o.
= + 90o.