Cylindrical projections

Cylindrical projections are a class of projections in which the surface of projection is a cylinder whose axis intercepts the centre of the generating sphere. The native coordinate system is such that the polar axis is coincident with the axis of the cylinder. Meridians and parallels are mapped onto a retangular grid. The projection is therefore described directly by formulae which return x, and y. All cylindricals have

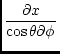
$\displaystyle \left\vert\vphantom{ \frac{\partial y}{\partial \theta} }\right.$ $\displaystyle {\frac{\partial y}{\partial \theta}}$ $\displaystyle \left.\vphantom{ \frac{\partial y}{\partial \theta} }\right\vert$ = $\displaystyle \left\vert\vphantom{ \frac{\partial x}{\cos \theta \partial \phi} }\right.$ $\displaystyle {\frac{\partial x}{\cos \theta \partial \phi}}$ $\displaystyle \left.\vphantom{ \frac{\partial x}{\cos \theta \partial \phi} }\right\vert$ ,

(36)

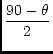
y $\displaystyle \propto$ r₀lntan $\displaystyle \left(\vphantom{ \frac{90 - \theta}{2} }\right.$ $\displaystyle {\frac{90 - \theta}{2}}$ $\displaystyle \left.\vphantom{ \frac{90 - \theta}{2} }\right)$ ,

(38)

Let an oblique coordinate system be denoted by ( $\phi{^\prime}$ , $\theta{^\prime}$ ), and let the coordinates of the pole [??? (0,0)] of the native coordinate system in the oblique system be ( $\phi{^\prime}_{0}$ , $\theta{^\prime}_{0}$ ). The meridian of the oblique system defined by $\phi{^\prime}$ = $\phi{^\prime}_{0}$ will be projected as a straight line segment; suppose it overlies the native meridian of $\phi$ = $\phi_{0}^{}$ in the same sense of increasing or decreasing latitude (to distinguish it from the native meridian on the opposite side of the pole), then the Euler angles for the transformation from ( $\phi{^\prime}$ , $\theta{^\prime}$ ) to ( $\phi$ , $\theta$ ) are

( $\displaystyle \Phi{^\prime}$ , $\displaystyle \Theta{^\prime}$ , $\displaystyle \Phi$ ) = ( $\displaystyle \phi{^\prime}_{0}$ - 90^o, $\displaystyle \theta{^\prime}_{0}$ , $\displaystyle \phi_{0}^{}$ - 90^o). (39)

Perspective cylindrical projections

In the general case the radius of the cylinder is $\lambda$ r₀, where r₀ is the radius of the generating sphere, and the point of projection is distant $\mu$ r₀ from the centre of the sphere. If $\mu$ $\neq$ 0 the point of projection moves around a circle of radius $\mu$ r₀ in the equatorial plane of the generating sphere depending on the meridian being projected. The case $\mu$ < 0 is allowable, however $\mu$ $\neq$ - $\lambda$ .

x	=	- r₀ $\displaystyle \lambda$ $\displaystyle \phi$ $\displaystyle {\frac{\pi}{180}}$ ,	(40)
y	=	r₀sin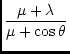 $\displaystyle \theta$ $\displaystyle \left(\vphantom{ \frac{\mu + \lambda}{\mu + \cos \theta} }\right.$ $\displaystyle {\frac{\mu + \lambda}{\mu + \cos \theta}}$ $\displaystyle \left.\vphantom{ \frac{\mu + \lambda}{\mu + \cos \theta} }\right)$ ,	(41)

For $\mu$ = 0, where the point of projection is at the centre of the generating sphere, the effect of $\lambda$ is to scale the projection uniformly in x and y.

$\displaystyle \phi$	=	- $\displaystyle {\frac{180 x}{\pi \lambda r_0}}$ ,	(42)
$\displaystyle \theta$	=	arg(1, $\displaystyle \eta$ ) + sin^-1 $\displaystyle \left(\vphantom{ \frac{\eta \mu}{\sqrt{\eta^2 + 1}} }\right.$ $\displaystyle {\frac{\eta \mu}{\sqrt{\eta^2 + 1}}}$ $\displaystyle \left.\vphantom{ \frac{\eta \mu}{\sqrt{\eta^2 + 1}} }\right)$ ,	(43)

Limits for the perspective cylindrical projections are determined by the value of $\mu$ rather than $\lambda$ which mainly affects the relative scaling of the x and y axes.

[ $\displaystyle \mu$ ( $\displaystyle \mu$ + $\displaystyle \lambda$ ) - $\displaystyle \lambda$ ]cos² $\displaystyle \theta$ + ( $\displaystyle \mu$ + $\displaystyle \lambda$ - 2 $\displaystyle \mu$ $\displaystyle \lambda$ )cos $\displaystyle \theta$ - $\displaystyle \mu^{2}_{}$ $\displaystyle \lambda$ = 0.

(45)

For $\mu$ = 0 the projection is conformal at the equator for all values of $\lambda$ . For $\mu$ = 1 the projection is conformal at latitudes $\theta$ = $\pm$ cos^-1 $\lambda$ , and this is the basis of Gall's projection.

Simple perspective cylindrical projection

In this simplest case of a perspective cylindrical projection the point of projection is at the centre of the generating sphere and the cylinder intersects the equator.

$\displaystyle \mu$	=	0,	(46)
$\displaystyle \lambda$	=	1,	(47)
x	=	- r₀ $\displaystyle \phi$ $\displaystyle {\frac{\pi}{180}}$ ,	(48)
y	=	r₀tan $\displaystyle \theta$ ,	(49)
$\displaystyle \phi$	=	- $\displaystyle {\frac{180 x}{\pi r_0}}$ ,	(50)
$\displaystyle \theta$	=	tan^-1 $\displaystyle \left(\vphantom{ \frac{y}{r_0} }\right.$ $\displaystyle {\frac{y}{r_0}}$ $\displaystyle \left.\vphantom{ \frac{y}{r_0} }\right)$ .	(51)

Limits: diverges at latitudes $\theta$ = $\pm$ 90^o.
Conformal at latitude $\theta$ = 0^o.

Gall's projection

This projection, which is conformal at latitudes $\theta$ = $\pm$ 45^o, minimizes distortions in the equatorial regions.

$\displaystyle \mu$	=	1	(52)
$\displaystyle \lambda$	=	$\displaystyle \sqrt{2}$ /2	(53)
x	=	- r₀ $\displaystyle \phi$ $\displaystyle {\frac{\sqrt{2} \pi}{360}}$ ,	(54)
y	=	r₀ $\displaystyle \left(\vphantom{ 1 + \frac{\sqrt{2}}{2} }\right.$ 1 + $\displaystyle {\frac{\sqrt{2}}{2}}$ $\displaystyle \left.\vphantom{ 1 + \frac{\sqrt{2}}{2} }\right)$ tan $\displaystyle \left(\vphantom{ \frac{\theta}{2} }\right.$ $\displaystyle {\frac{\theta}{2}}$ $\displaystyle \left.\vphantom{ \frac{\theta}{2} }\right)$ ,	(55)
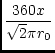$\displaystyle \phi$	=	- $\displaystyle {\frac{360 x}{\sqrt{2} \pi r_0}}$ ,	(56)
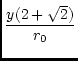
$\displaystyle \theta$	=	2tan^-1 $\displaystyle \left(\vphantom{ \frac{y ( 2 + \sqrt{2} )}{r_0} }\right.$ $\displaystyle {\frac{y ( 2 + \sqrt{2} )}{r_0}}$ $\displaystyle \left.\vphantom{ \frac{y ( 2 + \sqrt{2} )}{r_0} }\right)$ .	(57)

Lambert's equal area projection

This perspective projection is a specific instance of a subclass of non-perspective equal area cylindrical projections. See also generalized equal area cylindrical projections.

$\displaystyle \mu$	=	$\displaystyle \infty$ ,	(58)
$\displaystyle \lambda$	=	1,	(59)
x	=	- r₀ $\displaystyle \phi$ $\displaystyle {\frac{\pi}{180}}$ ,	(60)
y	=	r₀sin $\displaystyle \theta$ ,	(61)
$\displaystyle \phi$	=	- $\displaystyle {\frac{180 x}{\pi r_0}}$ ,	(62)
$\displaystyle \theta$	=	sin^-1 $\displaystyle \left(\vphantom{ \frac{y}{r_0} }\right.$ $\displaystyle {\frac{y}{r_0}}$ $\displaystyle \left.\vphantom{ \frac{y}{r_0} }\right)$ .	(63)

Non-perspective cylindrical projections

x = - r₀ $\displaystyle \phi$ $\displaystyle \left(\vphantom{ \frac{\pi}{180} }\right.$ $\displaystyle {\frac{\pi}{180}}$ $\displaystyle \left.\vphantom{ \frac{\pi}{180} }\right)$ ,

(64)

Plate Carreé projection

Also known as Cartesian projection, this projection is easy to construct and take measurements from.

y	=	r₀ $\displaystyle \theta$ $\displaystyle \left(\vphantom{ \frac{\pi}{180} }\right.$ $\displaystyle {\frac{\pi}{180}}$ $\displaystyle \left.\vphantom{ \frac{\pi}{180} }\right)$ ,	(66)
$\displaystyle \theta$	=	- $\displaystyle {\frac{180 y}{\pi r_0}}$ .	(67)

Mercator's projection

This is a conformal projection with the useful property that lines of constant bearing (rhumb lines) are projected as straight lines. Consequently, it has been widely used for navigational purposes.

y	=	r₀lntan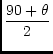 $\displaystyle \left(\vphantom{ \frac{90 + \theta}{2} }\right.$ $\displaystyle {\frac{90 + \theta}{2}}$ $\displaystyle \left.\vphantom{ \frac{90 + \theta}{2} }\right)$ ,	(68)
$\displaystyle \theta$	=	2tan^-1 $\displaystyle \left(\vphantom{ e ^ { \left ( \frac{y}{r_0} \right ) } }\right.$ e $\displaystyle \left.\vphantom{ e ^ { \left ( \frac{y}{r_0} \right ) } }\right)$ .	(69)

Generalized equal area cylindrical projection

Parallels are spaced so as to make the projection equal area, and scaled so as to make it conformal at latitudes $\theta$ = $\pm$ $\theta_{x}^{}$ . The area of a region on the projection is 1/cos² $\theta_{x}^{}$ times larger than that of the corresponding region on the generating sphere. The case with $\lambda$ = 1 is Lambert's projection.

y	=	r₀ $\displaystyle {\frac{\sin \theta}{\cos \theta_x^2}}$ ,	(70)
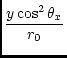
$\displaystyle \theta$	=	sin^-1 $\displaystyle \left(\vphantom{ \frac{y \cos^2 \theta_x}{r_0} }\right.$ $\displaystyle {\frac{y \cos^2 \theta_x}{r_0}}$ $\displaystyle \left.\vphantom{ \frac{y \cos^2 \theta_x}{r_0} }\right)$ .	(71)