Getting Started Documentation Glish Learn More Programming Contact Us
Version 1.9 Build 1556
News FAQ
Search Home

next up previous
Up: No Title Previous: Conic projections

Subsections

Conventional projections

Conventional projections are pure-mathematical constructions designed to map the entire sphere with minimal distortion.

The Euler angles for constructing oblique forms of these projections are specified in the same way as for the cylindrical projections, i.e. as

($\displaystyle \Phi{^\prime}$,$\displaystyle \Theta{^\prime}$,$\displaystyle \Phi$) = ($\displaystyle \phi{^\prime}_{0}$ - 90o,$\displaystyle \theta{^\prime}_{0}$,$\displaystyle \phi_{0}^{}$ - 90o). (108)

Sanson-Flamsteed (sinusoidal) projection

Parallels are equispaced and their length is chosen to make an equal area projection. It is, in fact, the equatorial case of Bonne's projection.


x = - r0$\displaystyle \phi$cos$\displaystyle \theta$$\displaystyle \left(\vphantom{ \frac{\pi}{180} }\right.$$\displaystyle {\frac{\pi}{180}}$ $\displaystyle \left.\vphantom{ \frac{\pi}{180} }\right)$, (109)
y = r0$\displaystyle \theta$$\displaystyle \left(\vphantom{ \frac{\pi}{180} }\right.$$\displaystyle {\frac{\pi}{180}}$ $\displaystyle \left.\vphantom{ \frac{\pi}{180} }\right)$, (110)
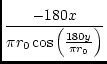$\displaystyle \phi$ = $\displaystyle {\frac{- 180 x}{\pi r_0 \cos \left ( \frac{180 y}{\pi r_0} \right )}}$, (111)
$\displaystyle \theta$ = $\displaystyle {\frac{180 y}{\pi r_0}}$. (112)

\epsffile{SansonFlamsteed.eps}

Limits: none.
Conformal at latitude $ \theta$ = 0 and at longitude $ \phi$ = 0.

Aitov's projection

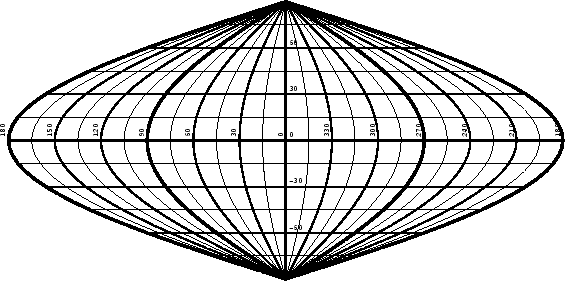
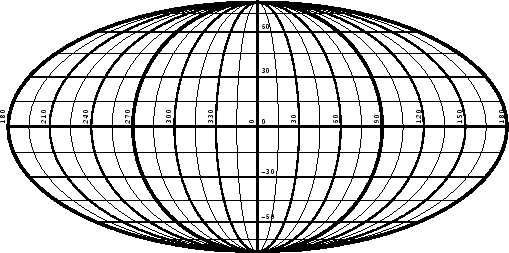
This projection is developed from the equatorial case of the zenithal equal area projection for a hemisphere. The equatorial scale and the longitude coverage are both doubled, thereby mapping the whole sphere while preserving the equal area property.

We will derive the equations for the projection here as an illustration of the construction of oblique projections, and also because the inverse equations are most easily derived by reversing the process.

The equations for the polar case of the zenithal equal area projection are (§2.2.2)


x'' = - r0$\displaystyle \sqrt{2 ( 1 - \sin \theta'' )}$sin$\displaystyle \phi{^\prime}{^\prime}$, (113)
y'' = - r0$\displaystyle \sqrt{2 ( 1 - \sin \theta'' )}$cos$\displaystyle \phi{^\prime}{^\prime}$, (114)

where double primes denote the native polar system and single primes will denote the equatorial system. Following the prescription given in §2 for constructing oblique projections, the coordinates of the pole of the native system in the oblique system are ($ \phi{^\prime}_{0}$,$ \theta{^\prime}_{0}$) = (0, 0), with ($ \phi{^\prime}{^\prime}_{0}$ = 0). The Euler angles for the transformation are therefore ($ \Phi{^\prime}$,$ \Theta{^\prime}$,$ \Phi{^\prime}{^\prime}$) = (90o, 90o, 90o). Thus


$\displaystyle \phi{^\prime}{^\prime}$ = 90o + arg(cos$\displaystyle \theta{^\prime}$sin$\displaystyle \phi{^\prime}$, sin$\displaystyle \theta{^\prime}$), (115)
$\displaystyle \theta{^\prime}{^\prime}$ = sin-1(cos$\displaystyle \theta{^\prime}$cos$\displaystyle \phi{^\prime}$), (116)

whence


cos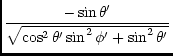$\displaystyle \phi{^\prime}{^\prime}$ = $\displaystyle {\frac{- \sin \theta'}{\sqrt{\cos^2 \theta' \sin^2 \phi' + \sin^2 \theta'}}}$, (117)
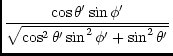sin$\displaystyle \phi{^\prime}{^\prime}$ = $\displaystyle {\frac{\cos \theta' \sin \phi'}{\sqrt{\cos^2 \theta' \sin^2 \phi' + \sin^2 \theta'}}}$, (118)
sin$\displaystyle \theta{^\prime}{^\prime}$ = cos$\displaystyle \theta{^\prime}$cos$\displaystyle \phi{^\prime}$. (119)

Setting (x', y') = (x'', y'') we have the equations for constructing the equatorial case of the zenithal equal area projection


x' = - r0$\displaystyle \alpha{^\prime}$cos$\displaystyle \theta{^\prime}$sin$\displaystyle \phi{^\prime}$, (120)
y' = r0$\displaystyle \alpha{^\prime}$sin$\displaystyle \theta{^\prime}$, (121)

where


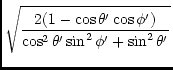$\displaystyle \alpha{^\prime}$ = $\displaystyle \sqrt{\frac{2 ( 1 - \cos \theta' \cos \phi')} {\cos^2 \theta' \sin^2 \phi' + \sin^2 \theta'}}$ (122)
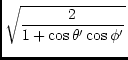  = $\displaystyle \sqrt{\frac{2}{1 + \cos \theta' \cos \phi'}}$. (123)

The equations for Aitov's projection may be deduced by making the substitutions


x = 2x', (124)
y = y', (125)
$\displaystyle \phi$ = 2$\displaystyle \phi{^\prime}$, (126)
$\displaystyle \theta$ = $\displaystyle \theta{^\prime}$, (127)

whence


x = -2r0$\displaystyle \alpha$cos$\displaystyle \theta$sin$\displaystyle {\frac{\phi}{2}}$, (128)
y = r0$\displaystyle \alpha$sin$\displaystyle \theta$, (129)

where

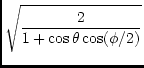$\displaystyle \alpha$ = $\displaystyle \sqrt{\frac{2}{1 + \cos \theta \cos ( \phi / 2 )}}$. (130)

These equations would be difficult to invert without prior knowledge of how they were obtained. However, it is a fairly simple matter to apply the construction process to the inverse equations for the zenithal equal area projection. From §2.2.2 we have


$\displaystyle \phi{^\prime}{^\prime}$ = arg(- y'', - x''), (131)
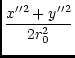
$\displaystyle \theta{^\prime}{^\prime}$ = sin-1$\displaystyle \left(\vphantom{ 1 - \frac{x''^2 + y''^2}{2 r_0^2} }\right.$1 - $\displaystyle {\frac{x''^2 + y''^2}{2 r_0^2}}$ $\displaystyle \left.\vphantom{ 1 - \frac{x''^2 + y''^2}{2 r_0^2} }\right)$. (132)

so that


cos$\displaystyle \phi{^\prime}{^\prime}$ = $\displaystyle {\frac{-y''}{R''}}$, (133)
sin$\displaystyle \phi{^\prime}{^\prime}$ = $\displaystyle {\frac{-x''}{R''}}$, (134)
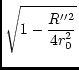cos$\displaystyle \theta{^\prime}{^\prime}$ = $\displaystyle {\frac{R''}{r_0}}$$\displaystyle \sqrt{1 - \frac{R''^2}{4 r_0^2}}$, (135)
sin$\displaystyle \theta{^\prime}{^\prime}$ = 1 - $\displaystyle {\frac{R''^2}{2 r_0^2}}$, (136)

where

R'' = $\displaystyle \sqrt{x''^2 + y''^2}$. (137)

The Euler angles for the transformation from the ($ \phi{^\prime}{^\prime}$,$ \theta{^\prime}{^\prime}$) system to the ($ \phi{^\prime}$,$ \theta{^\prime}$) system are the inverse of those presented previously, i.e. ($ \Phi{^\prime}{^\prime}$,$ \Theta{^\prime}{^\prime}$,$ \Phi{^\prime}$) = ($ \Phi{^\prime}$,$ \Theta{^\prime}$,$ \Phi{^\prime}{^\prime}$)-1 = (90o, - 90o, 90o), so


$\displaystyle \phi{^\prime}$ = 90o + arg(cos$\displaystyle \theta{^\prime}{^\prime}$sin$\displaystyle \phi{^\prime}{^\prime}$, - sin$\displaystyle \theta{^\prime}{^\prime}$), (138)
$\displaystyle \theta{^\prime}$ = sin-1(- cos$\displaystyle \theta{^\prime}{^\prime}$cos$\displaystyle \phi{^\prime}{^\prime}$), (139)

and substituting with (x'', y'') = (x', y') we have


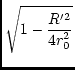$\displaystyle \phi{^\prime}$ = 90o + arg$\displaystyle \left(\vphantom{ \frac{-x'}{r_0} \sqrt{1 - \frac{R'^2}{4 r_0^2}} , \frac{R'^2}{2 r_0^2} - 1 }\right.$$\displaystyle {\frac{-x'}{r_0}}$$\displaystyle \sqrt{1 - \frac{R'^2}{4 r_0^2}}$,$\displaystyle {\frac{R'^2}{2 r_0^2}}$ - 1$\displaystyle \left.\vphantom{ \frac{-x'}{r_0} \sqrt{1 - \frac{R'^2}{4 r_0^2}} , \frac{R'^2}{2 r_0^2} - 1 }\right)$, (140)
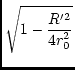
$\displaystyle \theta{^\prime}$ = sin-1$\displaystyle \left(\vphantom{ \frac{y'}{r_0} \sqrt{1 - \frac{R'^2}{4 r_0^2}} }\right.$$\displaystyle {\frac{y'}{r_0}}$$\displaystyle \sqrt{1 - \frac{R'^2}{4 r_0^2}}$ $\displaystyle \left.\vphantom{ \frac{y'}{r_0} \sqrt{1 - \frac{R'^2}{4 r_0^2}} }\right)$, (141)

where

R' = $\displaystyle \sqrt{x'^2 + y'^2}$. (142)

The inverse equations for Aitov's projection are then readily obtained by substituting


x' = x/2, (143)
y' = y, (144)
$\displaystyle \phi{^\prime}$ = $\displaystyle \phi$/2, (145)
$\displaystyle \theta{^\prime}$ = $\displaystyle \theta$, (146)

whence


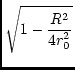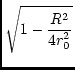
$\displaystyle \phi$ = 180o + 2arg$\displaystyle \left(\vphantom{ \frac{-x}{2 r_0} \sqrt{1 - \frac{R^2}{4 r_0^2}} , \frac{R^2}{2 r_0^2} - 1 }\right.$$\displaystyle {\frac{-x}{2 r_0}}$$\displaystyle \sqrt{1 - \frac{R^2}{4 r_0^2}}$,$\displaystyle {\frac{R^2}{2 r_0^2}}$ - 1$\displaystyle \left.\vphantom{ \frac{-x}{2 r_0} \sqrt{1 - \frac{R^2}{4 r_0^2}} , \frac{R^2}{2 r_0^2} - 1 }\right)$, (147)
$\displaystyle \theta$ = sin-1$\displaystyle \left(\vphantom{ \frac{y}{r_0} \sqrt{1 - \frac{R^2}{4 r_0^2}} }\right.$$\displaystyle {\frac{y}{r_0}}$$\displaystyle \sqrt{1 - \frac{R^2}{4 r_0^2}}$ $\displaystyle \left.\vphantom{ \frac{y}{r_0} \sqrt{1 - \frac{R^2}{4 r_0^2}} }\right)$, (148)

where

R = $\displaystyle \sqrt{x^2 / 4 + y^2}$. (149)

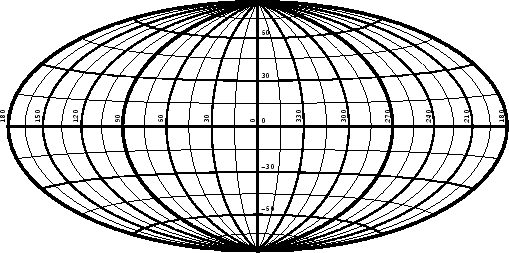
\epsffile{Aitov.eps}

Limits: none.
Conformal at the centre only.

Mollweide's projection

Meridians are projected as ellipses, parallels as straight lines spaced so as to make the projection equal area.


x = r0$\displaystyle \left(\vphantom{ \frac{\phi}{90} }\right.$$\displaystyle {\frac{\phi}{90}}$ $\displaystyle \left.\vphantom{ \frac{\phi}{90} }\right)$$\displaystyle \sqrt{2}$cos$\displaystyle \alpha$, (150)
y = r0$\displaystyle \sqrt{2}$sin$\displaystyle \alpha$, (151)
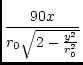$\displaystyle \phi$ = $\displaystyle {\frac{90 x}{r_0 \sqrt{2 - \frac{y^2}{r_0^2}}}}$, (152)
$\displaystyle \theta$ = sin-1$\displaystyle \left(\vphantom{ \frac{1}{90} \sin^{-1} \left ( \frac{y}{\sqrt{2} r_0} \right ) + \frac{y}{r_0} \sqrt{2 - \frac{y^2}{r_0^2}} }\right.$$\displaystyle {\textstyle\frac{1}{90}}$sin-1$\displaystyle \left(\vphantom{ \frac{y}{\sqrt{2} r_0} }\right.$$\displaystyle {\frac{y}{\sqrt{2} r_0}}$ $\displaystyle \left.\vphantom{ \frac{y}{\sqrt{2} r_0} }\right)$ + $\displaystyle {\frac{y}{r_0}}$$\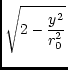displaystyle \sqrt{2 - \frac{y^2}{r_0^2}}$ $\displaystyle \left.\vphantom{ \frac{1}{90} \sin^{-1} \left ( \frac{y}{\sqrt{2} r_0} \right ) + \frac{y}{r_0} \sqrt{2 - \frac{y^2}{r_0^2}} }\right)$. (153)

where $ \alpha$ is given as the solution of the transcendental equation

sin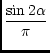$\displaystyle \theta$ = $\displaystyle {\frac{\alpha}{90}}$ + $\displaystyle {\frac{\sin 2 \alpha}{\pi}}$. (154)

\epsffile{Mollweide.eps}

Limits: none.

next up previous
Up: No Title Previous: Conic projections
Please send questions or comments about AIPS++ to aips2-request@nrao.edu.
Copyright © 1995-2000 Associated Universities Inc., Washington, D.C.
Return to AIPS++ Home Page
2006-10-15