
 News News |
 FAQ FAQ
|
 Search Search
|
 Home Home
|
| Getting Started | Documentation | Glish | Learn More | Programming | Contact Us |

| Version 1.9 Build 1556 |
|
Parallels are projected as arcs of circles. Projections for which the
parallels are concentric may be described by R![]() and A
and A![]() , where
R
, where
R![]() is the radius of the arc for latitude
is the radius of the arc for latitude ![]() . Then,
. Then,
| x | = | - R |
(72) |
| y | = | - R |
(73) |
The requirement for conformality is
|
|
(74) |
In the special case satisfied by one-, and two-standard conic projections
|
|
(75) |
a constant known as the constant of the cone, this differential equation has the general solution
R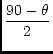
|
(76) |
where ![]() is a constant. This solution is used to construct orthomorphic
conic projections. The apical angle of the projected cone is 2
is a constant. This solution is used to construct orthomorphic
conic projections. The apical angle of the projected cone is 2![]() C where
C where
| C | = | (77) | |
| = | 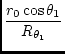 |
(78) | |
| = | 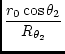 |
(79) |
where ![]() (and
(and ![]() ) is the latitude of the standard parallel(s).
) is the latitude of the standard parallel(s).
The standard parallel is at latitude ![]() . All of the diagrams
presented here have been computed for
. All of the diagrams
presented here have been computed for
![]() = 45o.
= 45o.
| R |
= | r0[cot |
(80) |
| A |
= | (81) |
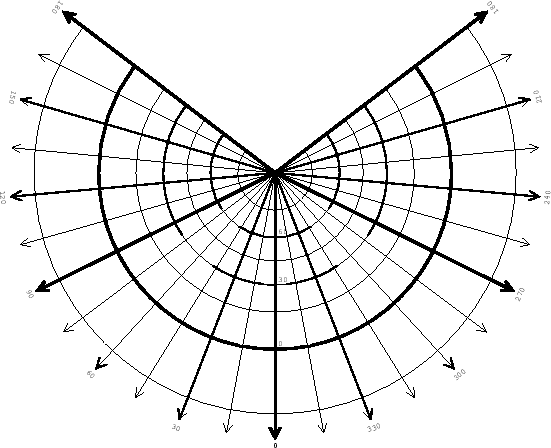
Limits: diverges at latitude
![]() =
= ![]() - 90o.
- 90o.
Conformal at latitude ![]() .
.
Constant of the cone:
C = sin![]() .
.
The spacing between parallels is true.
| R |
= | r0[cot |
(82) |
| A |
= | (83) |
Limits: none.
Conformal at latitude ![]() .
.
Constant of the cone:
C = sin![]() .
.
R![]() is defined so that the area between any two parallels on the
projection is true.
is defined so that the area between any two parallels on the
projection is true.
| R |
= | r0 |
(84) |
| A |
= | (85) |
Limits: none.
Conformal at latitude ![]() .
.
Constant of the cone:
C = sin![]() .
.
| R |
= | r0cot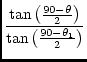
|
(86) |
| A |
= | (87) |
Limits: diverges at latitude
![]() = - 90o.
= - 90o.
Conformal at all points.
Constant of the cone:
C = sin![]() .
.
The standard parallels are at latitudes ![]() and
and ![]() ,
,
![]() <
< ![]() . All of the diagrams presented here have been computed
for
. All of the diagrams presented here have been computed
for
![]() = 30o and
= 30o and
![]() = 60o.
= 60o.
| R |
= | r0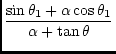 |
(88) |
| A |
= | (89) |
where
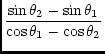
|
(90) |
Note that
| sin |
= | sin |
(91) |
| = | 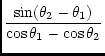 |
(92) |
Limits: diverges at latitude
![]() = tan-1(-
= tan-1(- ![]() ).
).
Conformal at latitude
![]() = tan-1(1/
= tan-1(1/![]() ).
).
Constant of the cone:
C = (1 + ![]() )-
)- ![]() .
.
The spacing between parallels is true.
| R |
= | r0 |
(93) |
| A |
= | (94) |
where
|
|
(95) |
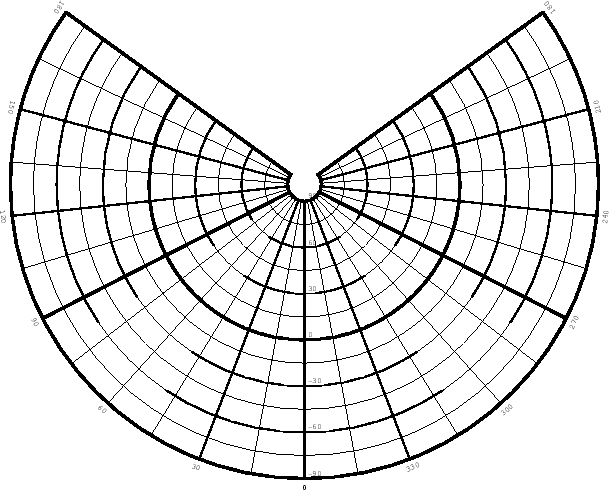
Limits: none.
Conformal at latitudes ![]() and
and ![]() .
.
Constant of the cone:
![]() /[
/[![]() (
(![]() -
- ![]() )].
)].
| R |
= | 2r0 |
(96) |
| A |
= | (97) |
where
|
|
(98) |
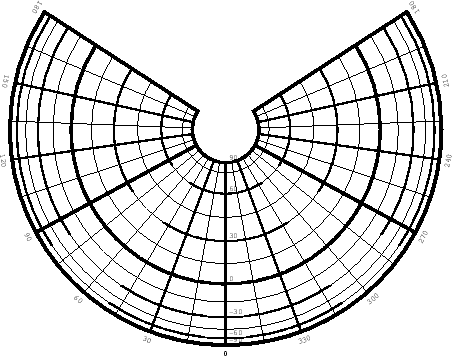
Limits: none.
Conformal at latitudes ![]() and
and ![]() .
.
Constant of the cone:
![]() /2.
/2.
| R |
= | r0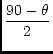
|
(99) |
| A |
= | (100) |
where
| = | ![$\displaystyle {\frac{\cos \theta_1}{C \left [
\tan \left ( \frac{90 - \theta_1}{2} \right )
\right ]^C}}$](img168.gif) |
(101) | |
| = | ![$\displaystyle {\frac{\cos \theta_2}{C \left [
\tan \left ( \frac{90 - \theta_2}{2} \right )
\right ]^C}}$](img169.gif) |
(102) | |
| C | = | ![$\displaystyle {\frac{\ln \left ( \frac{\cos \theta_2}{\cos \theta_1} \right )}{...
...heta_2}{2} \right )}
{\tan \left ( \frac{90 - \theta_1}{2} \right )}
\right ]}}$](img170.gif) |
(103) |
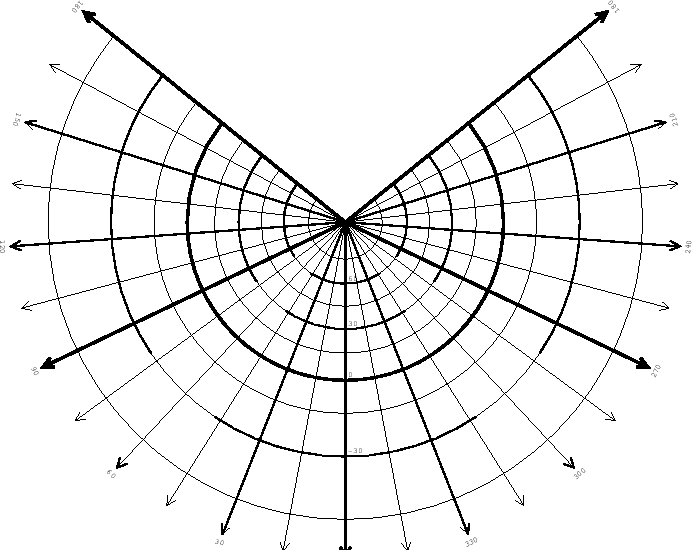
Limits: diverges at latitude
![]() = - 90o.
= - 90o.
Conformal at all points.
Parallels are concentric equidistant arcs of circles of true length. The
diagram presented here has been computed for
![]() = 45o.
= 45o.
| R |
= | r0(cot |
(104) |
| A |
= | r0 |
(105) |

Limits: none.
Conformal at latitude ![]() and along the central meridian.
and along the central meridian.
Every parallel is projected as standard, i.e. as arcs of circles of radius
rcot![]() at their true length,
2
at their true length,
2![]() rcos
rcos![]() , and correctly
divided. The scale along the central meridian is true, consequently the
parallels are not concentric.
, and correctly
divided. The scale along the central meridian is true, consequently the
parallels are not concentric.
| x | = | r0cot |
(106) |
| y | = | r0{cot |
(107) |
Limits: none.
Conformal along the central meridian.