THE FULL MEASUREMENT EQUATION

For k `real' incoherent sources, observed with a `real' telescope, equ 1 becomes:

$\displaystyle \vec{V}_{{\sf i}{\sf j}}$ = $\displaystyle {\frac{1}{\Delta{\sf t}\Delta{\sf f}}}$ $\displaystyle \int$ d $\displaystyle \sf t$ $\displaystyle \int$ d $\displaystyle \sf f$ $\displaystyle \sum_{{k}}^{}$ $\displaystyle {\frac{1}{\Delta{\sf l}\Delta{\sf m}}}$ $\displaystyle \int$ d $\displaystyle \sf l$ d $\displaystyle \sf m$ $\displaystyle \sf J_{{\sf i}}^{}$ $\displaystyle \otimes$ $\displaystyle \sf J_{{\sf j}}^{\ast}$ $\displaystyle \sf S$ $\displaystyle \vec{I}\,$ ( $\displaystyle \sf l$ , $\displaystyle \sf m$ )

(6)

The visibility vector $\vec{V}_{{\sf i}{\sf j}}$ is integrated over the extent of the sources ( $\int$ d $\sf l$ d $\sf m$ ), over the integration time ( $\int$ d $\sf t$ ) and over the channel bandwidth ( $\int$ d $\sf f$ ). Integration over the aperture ( $\int$ d $\sf u$ d $\sf v$ ) is taken care of by the primary beam properties.

There are only four integration coordinates, whose units are determined by the flux density units in which $\vec{I}\,$ is expressed: energy/sec/Hz/beam. These coordinates define a 4-dimensional `integration cell'. If the variation of $\vec{V}\,$ ( $\sf f$ , $\sf t$ , $\sf l$ , $\sf m$ ) is linear over this cell, integration is not necessary:

$\displaystyle \vec{V}_{{\sf i}{\sf j}}$ = $\displaystyle \sum_{k}^{}$ $\displaystyle \vec{V}_{0k}$ ( $\displaystyle \sf f_{0}^{}$ , $\displaystyle \sf t_{0}^{}$ , $\displaystyle \sf l_{0}^{}$ , $\displaystyle \sf m_{0}^{}$ )

(7)

in which $\vec{V}_{0k}$ is the value for source k at the centre of the cell, for $\Delta$ $\sf f$ = 1 Hz and $\Delta$ $\sf t$ = 1 sec. If the variation of $\vec{V}\,$ ( $\sf f$ , $\sf t$ , $\sf l$ , $\sf m$ ) over the cell can be approximated by a polynomial of order $\leq$ 3, then it is sufficient to calculate only the 2nd derivative(s) at the centre of the cell:

$\displaystyle \vec{V}^{int}$ = $\displaystyle \sum_{k}^{}$ $\displaystyle \vec{V}_{0k}$ + $\displaystyle {\textstyle\frac{1}{12}}$ ( $\displaystyle {\frac{\partial^{2}{{\vec{V}}_{0k}}}{\partial{{\sf f}}^{2}}}$ ( $\displaystyle \Delta$ $\displaystyle \sf f$ )² + $\displaystyle {\frac{\partial^{2}{{\vec{V}}_{0k}}}{\partial{{\sf t}}^{2}}}$ ( $\displaystyle \Delta$ $\displaystyle \sf t$ )² + $\displaystyle {\frac{\partial^{2}{{\vec{V}}_{0k}}}{\partial{{\sf l}}^{2}}}$ ( $\displaystyle \Delta$ $\displaystyle \sf l$ )² + $\displaystyle {\frac{\partial^{2}{{\vec{V}}_{0k}}}{\partial{{\sf m}}^{2}}}$ ( $\displaystyle \Delta$ $\displaystyle \sf m$ )²)

(8)

Here it is assumed that the 2nd derivatives are be constant over the cell, i.e. the cross-derivatives 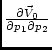${\frac{\partial{\vec{V}}_{0}}{\partial p_1 \partial p_2}}$ are zero.

interferometer-based effects

Until now, we have assumed that all instrumental effects could be factored into feed-based contributions, i.e. we have ignored any interferometer-based effects. This is justified for a well-designed system, provided that the signal-to-noise ratio is large enough (thermal noise causes interferometer-based errors, albeit with a an average of zero). However, if systematic errors do occur, they can be modelled:

$\displaystyle \vec{V}_{{\sf i}{\sf j}}^{'}$ = $\displaystyle \sf X_{{\sf i}{\sf j}}^{}$ ( $\displaystyle \vec{A}_{{\sf i}{\sf j}}$ + $\displaystyle \sf M_{{\sf i}{\sf j}}^{}$ $\displaystyle \vec{V}_{{\sf i}{\sf j}}$ )

(9)

The 4 x 4 diagonal matrix $\sf X$ , the `Correlator matrix', represents interferometer-based corrections that are applied to the uv-data in software by the on-line system. Examples are the Van Vleck correction. In the newest correlators, it approaches a constant ( $\sf x$ ).

$\displaystyle \sf X_{{\sf i}{\sf j}}^{}$ = $\displaystyle \left(\vphantom{\begin{array}{rrrr} {\sf x}_{{\sf i}{\sf p}\,{\s... ...\\ 0 & 0 & 0 & {\sf x}_{{\sf i}{\sf q}\,{\sf j}{\sf q}} \end{array}}\right.$ $\displaystyle \begin{array}{rrrr} {\sf x}_{{\sf i}{\sf p}\,{\sf j}{\sf p}}& 0 ... ...f p}}& 0\\ 0 & 0 & 0 & {\sf x}_{{\sf i}{\sf q}\,{\sf j}{\sf q}} \end{array}$ $\displaystyle \left.\vphantom{\begin{array}{rrrr} {\sf x}_{{\sf i}{\sf p}\,{\s... ...\\ 0 & 0 & 0 & {\sf x}_{{\sf i}{\sf q}\,{\sf j}{\sf q}} \end{array}}\right)$ $\displaystyle \approx$ $\displaystyle \sf x$ $\displaystyle \cal {U}$

(10)

The 4 x 4 diagonal matrix $\sf M$ represents multiplicative interferometer-based effects.

$\displaystyle \sf M_{{\sf i}{\sf j}}^{}$ = $\displaystyle \left(\vphantom{\begin{array}{rrrr} {\sf m}_{{\sf i}{\sf p}\,{\s... ...\\ 0 & 0 & 0 & {\sf m}_{{\sf i}{\sf q}\,{\sf j}{\sf q}} \end{array}}\right.$ $\displaystyle \begin{array}{rrrr} {\sf m}_{{\sf i}{\sf p}\,{\sf j}{\sf p}}& 0 ... ...f p}}& 0\\ 0 & 0 & 0 & {\sf m}_{{\sf i}{\sf q}\,{\sf j}{\sf q}} \end{array}$ $\displaystyle \left.\vphantom{\begin{array}{rrrr} {\sf m}_{{\sf i}{\sf p}\,{\s... ...\\ 0 & 0 & 0 & {\sf m}_{{\sf i}{\sf q}\,{\sf j}{\sf q}} \end{array}}\right)$ $\displaystyle \approx$ $\displaystyle \cal {U}$

(11)

The 4-element vector $\vec{A}_{{\sf i}{\sf j}}^{}$ represents additive interferometer-based effects. Examples are receiver noise, and correlator offsets.

$\displaystyle \vec{A}_{{\sf i}{\sf j}}$ = $\displaystyle \left(\vphantom{\begin{array}{c} {\sf a}_{{\sf i}{\sf p}\,{\sf j... ...f j}{\sf p}}\\ {\sf a}_{{\sf i}{\sf q}\,{\sf j}{\sf q}} \end{array}}\right.$ $\displaystyle \begin{array}{c} {\sf a}_{{\sf i}{\sf p}\,{\sf j}{\sf p}}\\ {... ... q}\,{\sf j}{\sf p}}\\ {\sf a}_{{\sf i}{\sf q}\,{\sf j}{\sf q}} \end{array}$ $\displaystyle \left.\vphantom{\begin{array}{c} {\sf a}_{{\sf i}{\sf p}\,{\sf j... ...f j}{\sf p}}\\ {\sf a}_{{\sf i}{\sf q}\,{\sf j}{\sf q}} \end{array}}\right)$ $\displaystyle \approx$ $\displaystyle \vec{0}\,$

(12)

In some cases, interferometer-based effects can be calibrated, e.g. when they appear to be constant in time. It will be interesting to see how many of them will disappear as a result of better modelling with the Measurement Equation. In any case, it is desirable that the cause of interferometer-based effects is properly understood (simulation!).

THE FULL MEASUREMENT EQUATION

Summing and averaging

interferometer-based effects