componentmodels

Description The ``component models'' module contains tools and functions which define and manipulate components. Components represent the sky brightness as a function of position on the sky and observing frequency. The main tool in this module is the componentlist tool which provides functions for manipulating groups of components.

Components are a complimentary alternative to representing the sky brightness with an image. They are useful alternative when:

The field contains weak features in the presence of very bright features. Often residual errors from these bright features prevent the detection or analysis of the weak features. One way to avoid this is to model the bright features using a componentlist and then subtract them in the (u, v) domain.
The data is limited in quantity and/or contains significant errors or noise. Imaging under these circumstances is difficult and often the user must resort to modeling the sky brightness to reduce the number of free parameters and incorporate additional prior information.

Other tools within aips++, use components and aid in the above tasks. The two most important are:

imager: This tool can subtract componentlists in the (u, v) domain.
imagefitter: This tool can generate componentlists by fitting to specified regions of an image.

Component Description

Components have a number of properties which can be categorised as relating to either its flux, shape or spectrum.

Flux Properties A fundamental property of a component is its flux or integrated intensity^1.1. This can be measured in any units which are dimensionally equivalent to the Jansky (W/m²/Hz).

The flux of a component always has all polarisations defined and hence four numbers are used^1.2 to represent its value. The most common polarisation representation used is the Stokes parameters of I, Q, U, V. Two alternative representations are provided called ``circular'' and ``linear''.

When the circular representation is used the flux values are those that would be seen by detectors that are sensitive to right (R) and left (L) handed circular polarisation. They represent, in order, the RR, RL, LR, LL correlation products.

When the linear representation is used the flux values are those that would be seen if the detectors were sensitive to orthogonal linear polarisations. They represent, in order, the XX, XY, YX, YY correlation products where the parallactic angle is assumed to be zero.

When using the circular or linear representations the flux values will often be complex numbers and are always returned as such. Conversely when specifying the flux using the circular or linear representation four complex numbers are used. Unless some additional constraints are placed on these values e.g, RL = cong(LR) and imag(RR) = imag(LL) = 0, it will be possible to generate components where the flux, when converted to the Stokes representation, is not real. This is not considered an error however such components are not considered ``physical''. The is_physical function can be used to test when a component has values that could not correspond to the actual sky brightness.

When using the Stokes representation the flux values are always returned as real numbers. This value is a truncation, with the imaginary part discarded, of the internal complex value. Because the value is, regardless of the polarisation representation, stored as a complex value no information is lost when inter-converting between different polarisation representations

Shape Properties The shape properties of a component describe the variation of brightness as a function of the position on the sky. The shape properties are split into ones describing the functional variation and ones describing the position of a reference point on the sky. Components can have one of three shapes; point, Gaussian or disk. For all these shapes the reference point, which is a direction measure, defines the direction of the 'centre' of the component.

Both the disk and Gaussian shapes need additional parameters to completly define their shape. These parameters are the width of the major axis, the width of the minor axis and the position angle of the major axis. All these parameter are specified with angular quantities, and the width is the full-width at half-maximum. The major axis is constrained to being no smaller that the minor axis. The position angle is, following the standard astronomical convention, zero when the major axis is aligned North-South and increases when the northern tip of the major axis rotates to the East.

A point component is a special case of a Gaussian or a disk component with a very small major and minor axis width. It is treated separately both because it is very common in astronomy and because the knowledge that that the widths are infinitesimal allows important assumptions to be made when manipulating these components. The major axis, minor axis and position angle parameters are discarded for point components.

Spectral Properties The spectral properties of a component describe the variation of flux as a function of the observing frequency/wavelength. The spectral properties are split into ones describing the flux variation and ones describing a reference frequency. At the reference frequency the flux of the component is the value defined by the flux properties described above. At other frequencies it may differ. The reference frequency has a reference frame associated with it ie., it is a frequency measure. The frequency variation of a component can either be constant, or vary with a power law ie., it has a spectral index.

If the spectral properties specify that the flux varies depending on a spectral index an additional parameters is required. This is the spectral index (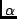). Then the spectral variation is then described by:

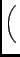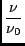
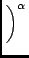I	=	I₀ $\displaystyle \left(\vphantom{\frac{\nu}{\nu_0}}\right.$ $\displaystyle {\frac{\nu}{\nu_0}}$ $\displaystyle \left.\vphantom{\frac{\nu}{\nu_0}}\right)^{\alpha}_{}$
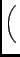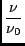
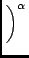Q	=	Q₀ $\displaystyle \left(\vphantom{\frac{\nu}{\nu_0}}\right.$ $\displaystyle {\frac{\nu}{\nu_0}}$ $\displaystyle \left.\vphantom{\frac{\nu}{\nu_0}}\right)^{\alpha}_{}$
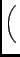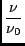
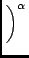U	=	U₀ $\displaystyle \left(\vphantom{\frac{\nu}{\nu_0}}\right.$ $\displaystyle {\frac{\nu}{\nu_0}}$ $\displaystyle \left.\vphantom{\frac{\nu}{\nu_0}}\right)^{\alpha}_{}$
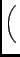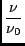
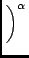V	=	V₀ $\displaystyle \left(\vphantom{\frac{\nu}{\nu_0}}\right.$ $\displaystyle {\frac{\nu}{\nu_0}}$ $\displaystyle \left.\vphantom{\frac{\nu}{\nu_0}}\right)^{\alpha}_{}$

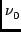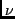where I₀, Q₀, U₀, V₀ is the flux at the reference frequency () and is the specified frequency.

Current Capabilities The component models module can currently do the following operations, all of them through the componentlist tool:

1.: Create an empty list of components and add or remove user specified components from the list.
2.: Create a list of components from an ascii file.
3.: Save the list to disk and read it back.
4.: Return the flux of the list in any user specified direction.
5.: Sort the components using a number of criteria.

In addition there is a component editor that allows the user to view and edit the parameters of a component through a graphical user interface.

See Also

Concepts from the measures module are used throughout this module.

Tools

`componenteditor`	`A graphical user interface for displaying & editing a component.`
`componentlist`	`A tool for the manipulation of groups of components`

Functions

is_componentlist Is the argument a componentlist tool?

Next: componentlist - Tool Up: Synthesis Previous: calibrater.done - Function Contents Index

componentmodels - Module