
 News News |
 FAQ FAQ
|
 Search Search
|
 Home Home
|
| Getting Started | Documentation | Glish | Learn More | Programming | Contact Us |

| Version 1.9 Build 1488 |
|
Mark Holdaway
The Fourier transform relationship between the Fourier plane and the image plane must include the primary beam:
|
V(u) = |
(4.1) |
Hence, given the image, it is trivial to simulate the corresponding data. However, given the data and desiring the image, we have an inverse problem to solve.
Early attempts at mosaicing treated each field independently, deconvolving and self-calibrating each, and then sewing the overlapping fields' images together via the basic mosaicing equation:
I(x) = 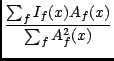 . .
|
(4.2) |
However, Cornwell (1988) demonstrated that superior results can be achieved via a simultaneous deconvolution of the data from all the fields. This simultaneous deconvolution was achieved by using maximum entropy (MEM) or maximum emptiness as a solution engine to solve the inverse problem. Total power could be added as additional fields with their own primary beam. However, MEM's positivity bias, which is detrimental to low SNR imaging, and its lukewarm reception from radio astronomers led to a search for other algorithms to image multi-field data.
Sault et al. (1996) have implemented mosaicing algorithms which can use either CLEAN or MEM for simultaneous deconvolution.
Cornwell, Holdaway, and Uson (1994) proposed a novel mosaicing algorithm for the upcoming millimeter array (MMA): generate the mosaic of the dirty images and a single approximate point-spread function (PSF), and then proceed with any conventional single field deconvolution algorithm. For the MMA's high-quality Fourier-plane coverage and similar PSF's for all fields in the mosaic, this approach was not limited by the differences in the approximate PSF and each field's actual PSF until the possible image dynamic range exceed a few hundred to one.
AIPS++ takes this approach to mosaicing a step further: perform an incremental deconvolution of the residuals with the approximate PSF, with an exact subtraction of the cumulative model brightness distribution at the end of each incremental ``major cycle'' (similar in concept to the major cycles of the Clark CLEAN).
If all of the fields are observed with many short snapshots over and over again (this is the usual way to make a mosaic observation) then each field will have similar Fourier coverage and hence similar synthesized beams. An approximate PSF can be created which is a fairly good match to the actual PSF of each of the fields. Also, if the sky-coverage of the observed fields is Nyquist or better, then the approximate, shift-invariant PSF will be a reasonable match to the actual PSF of sources at various locations across the mosaic. The residual visibilities from each field can be transformed and mosaiced to make a single residual mosaic image. This mosaic image can be deconvolved with the deconvolution method of your choice; for example, with Clark CLEAN, Multiscale CLEAN, maximum entropy, or maximum emptiness.
The deconvolution algorithm cannot deconvolve arbitrarily deeply, because at some level the discrepancies between our approximate shift-invariant PSF and the true PSF at any location in the image will become apparent, and we will start ``cleaning'' error flux. Hence, we need to stop deconvolving when we have gotten down to the level of these PSF discrepancies. At this point, we take the part of the model brightness distribution we have just deconvolved and calculate model visibilities (using the measurement equation) and subtract them from the (corrected) data visibilities. To the extent that the primary beam and sky pointing are exact, the visibility subtraction is also exact. The residual visibilities can then be re-mosaiced, but the peak residual is at a much lower level. The process of deconvolving with the approximate, shift-invariant PSF then continues, and another increment to the model brightness distribution is formed, removed from the remaining residual visibilities, and added to the cumulative model brightness distribution. Borrowing from the Clark CLEAN's terminology, we call each cycle of incremental deconvolution and exact visibility subtraction a ``major cycle''.
If the major cycles are properly controlled, there are potential advantages to incrementally deconvolving with an approximate PSF. For one, we are doing a regular single image deconvolution, so we are free to pick whatever algorithm we like (though NNLS has not been implemented in the multi-field context). Second, we are spending less CPU doing FFTs. In the Cornwell (1988) MEM-based mosaicing approach, each field needed a couple of FFT's for each iteration. In our incremental deconvolution using MEM, the entire image needs a couple of FFTs per iteration (independent of the number of fields), plus a couple of FFTs per field per major cycle. As there are several MEM iterations per major cycle, we usually come out ahead using the incremental deconvolution.
There are a number of simple things you need to do so that your mosaic is successful. Its easy to forget them, though, so we'll remind you.
Mosaicing is a time consuming process, so it will be worthwhile to make a restricted version of the mosaic first. For example, you may want to just image a few fields at lower resolution to reduce the number of pixels you are imaging. Eventually, you will want to image most or all of the observed fields.
imgr.setdata(fieldid=1:4) # Select first 4 fields
One of the fields must be specified in tool function Imager.setimage to provide the direction of the resultant image's reference pixel. For example, with a 25 pointing (5 x 5 raster) observation, field 13 could be the central field:
imgr.setimage(nx=256, ny=256, cellx="3arcsec",
celly="3arcsec", stokes="I", fieldid=13)
Or if a given position is wanted as the image center, then the default measures tool can be used in conjunction with setimage as follows:
imageCenter := dm.direction('J2000', '19h30m50', '-20d32m45.4')
imgr.setimage(nx=256, ny=256, cellx="3arcsec",
celly="3arcsec", stokes="I",
doshift=T, phasecenter=imageCenter)
Setting doshift=T tells the software to use the value specified in the phasecenter argument.
Currently, the deconvolution methods of choice for multi-field applications, namely Multi-scale CLEAN and maximum emptiness or entropy, do not treat Stokes I and V simultaneously.
Remember to tell Imager to use the voltage pattern (primary beam). If you don't, the image will be horribly confused. This is because we must account for the voltage pattern when imaging the same location on the but from different pointings.
imgr.setvp(dovp=T, usedefaultvp=T, dosquint=F).
If you don't like the default voltage pattern (provided for a range of telescopes; see Imager.setvp), you can specify your own voltage pattern and bind it to the telescopes in your MeasurementSet by using the Vpmanager (voltage pattern manager). The Vpmanager will produce a table describing the different telescopes' voltage patterns, and this table can be used by Imager via the setvp tool function.
imgr.setvp(dovp=T, usedefaultvp=F, vptable='MY.VP.TABLE').
The beam squint for certain telescopes (like the VLA) has been included in the default voltage pattern models. It is not relevant for other telescopes (like the ATCA). Beam squint can also be adjusted with the Vpmanager. For the voltage pattern application to include the effects of beam squint, reapplied in parallactic angle increments of 10 degrees, try
imgr.setvp(dovp=T, usedefaultvp=T, dosquint=T, parangleinc='10deg')
Note that the beam squint conventions have not been thoroughly tested, and could be backwards in orientation.
Extra-information:
Setting the use of a gridder. The default is to
use the normal gridding machine that use a spheroidal function in the
gridding process. Otherwise for mosaicing we can use the fourier
transform of primary beam as the gridding function. We recommend
this, as in the future this is the way to go to calibrate/correct
primary beam errors (e.g pointing errors or pb assymetry etc).
For now it is recommended that you set the gridder to mosaic by using the function setoptions.
imgr.setoptions(ftmachine='mosaic')
If you use ``uniform'' or ``briggs'' weighting, the weighting details will depend upon the way the data are gridded. However, if all fields are specified in function setdata, then the weights from all fields will be gridded onto a single grid for the purposes of calculating the weights. This is probably not what you want to do. Rather, it may make more sense to weight the data on a field-by-field basis:
for (myfield in [1:25]) {
imgr.setdata( fieldid=myfield ) # Weight each field separately
imgr.weight(type="uniform")
}
#
imgr.setdata( fieldid=[1:25] ) # Now select all fields
We are finally ready to image and deconvolve. You can use either imager's CLEAN or MEM functions. Only algorithms with the ``mf'' prefix will perform multi-field imaging correctly (i.e. algorithm ``clark'' will grid the data from all specified fields onto the same grid, resulting in a very confused image indeed. CLEAN's mosaicing methods include mfclark, mfhogbom, and mfmultiscale, while MEM's mosaicing methods include mfentropy and mfemptiness.
The key to making the incremental deconvolution in AIPS++ multi-field imaging successful lies in controlling just how deeply we deconvolve in the major cycles. The control parameters discussed here can be set with Imager.setmfcontrol. If we deconvolve too deeply with the approximate PSF, we will spin our wheels while adjacent fields with slightly different PSF sidelobes argue over where the low level model flux belongs; the answer will of course be in error, we will mis-subtract from the data visibilities, and we will have to correct our error in the early stages of the next major cycle of incremental deconvolution. If we don't deconvolve deeply enough in each major cycle, there will be more major cycles, which are dominated by the exact model subtraction.
One can see fairly easily if one is cleaning too deeply or not cleaning deeply enough in a given major cycle by looking at the plots given when the argument displayprogress=T (in tool function clean). When trying to clean too deeply, the peak residual level towards the end of a major cycle will flatten out (or may even increase and diverge) for many iterations. At the start of the next major cycle, the peak residual level will begin at a higher level than at the end of the previous major cycle. (This can be especially true for mosaicing with multi-scale clean, where the approximate PSF may actually be a pretty poor match for the true PSF's on the larger size-scales). If all is well, this major cycle will still get to a lower peak residual than the previous one. However, stopping the major cycles sooner will prevent us from spinning our wheels, resulting in a comparable deconvolved image in fewer iterations.
Eventually, there will probably be a smarter, more automatic way to determine if we need to stop the current major incremental deconvolution cycle. Right now, the tools are simple, but easy to use. If the progress display indicates that ending the major cycle sooner is appropriate, we can do that in one of two ways:
In addition to these cycle control parameters, which are applicable to mosaicing with CLEAN, Multi-Scale CLEAN, MEM, or Maximum Emptiness, there are two more control arguments set by tool function imager.setmfcontrol which are applicable only to Multi-Scale CLEAN. These are stoplargenegatives and stoppointmode, which are discussed below.
See the basic Imaging for multi-scale basics.
Sometimes in the first few iterations of Multi-scale CLEAN in the mosaicing context, the largest scale will be dominated by large negative residuals (i.e. this is just the negative bowl, integrated over the area of the largest clean-component scale). One way to fix this is to make the largest scale smaller. Another way is to use a tighter mask which excludes finding large scale components in the bowl region. And a third, ad hoc way is to stop the major cycle when a negative component is found on the largest scale. This allows the exact subtraction to proceed, often resulting in a reduced bowl level. Stopping the major cycle upon encountering a negative component on the largest scale should only be performed on the first few cycles, as during subsequent cycles small amplitude large scale components may be required to make adjustments in the image. The number of cycles for which stopping when a negative component is found on the largest scale can be controlled by the parameter stoplargenegatives in imager.setmfcontrol. As smaller scales may require negative components to correct for errors made by ``over-cleaning'' in the larger cycles, no restriction should be placed on negative components from smaller size scales.
myimager.setvp(dovp=T, usedefaultvp=T); myimager.setoptions(ftmachine='mosaic'); myimager.setscales(scalemethod='uservector', uservector=[0,3,10,30]) myimager.setmfcontrol(stoplargenegatives=3); myimager.clean(algorithm='mfmultiscale', niter=500, gain=0.2, model='modelim') In the above example we tell the multiscale clean to stop the multiscale process after it gets 3 negative components on the largest scale selected.
If there are bright unresolved or barely resolved sources in the field, it may be advantageous to perform a Clark Clean down to the level of the peak extended emission, or include a component list in the model, because MEM does not work well on bright point-like sources.
The maximum entropy/emptiness algorithm has been modified to fit into the incremental deconvolution/major cycle framework adopted by mosaicing in AIPS++. These algorithms deal with both the incremental brightness distribution, which it seeks to solve given the approximate PSF and the residual mosaic image, and the cumulative brightness distribution for the calculation of the entropy function and its gradients. When maximum entropy starts up, it typically takes the algorithm four or five iterations to ``find itself'' and get the control parameters set to achieve the proper balance between the gradients of the entropy and the chi squared. Once a good balance is struck, the algorithm makes marked progress towards convergence. At the end of a major cycle, the relevant control parameters are saved and used for the next major cycle.
If several different models or images are contributing to the model visibilities, the a visibility plane subtraction must be used. However, if a single model image covering all observed fields is used, as is usually the case with mosaicing, then it is more efficient to bypass the degridding and gridding operations and just calculate the residual images for each field by a convolution with each field's true PSF.
Sometimes flux from a confusing source will ``leak in'' through the outer sidelobes of the primary beam. This is a vexing problem, as the outer sidelobes are not in the primary beam model, the confusing source will not be removed from the data or corrected visibilities in the usual mosaicing algorithm, and its sidelobes will persist, possibly spoiling the dynamic range of other regions in the mosaiced image. In addition, each field will experience the outlying confusing source at a different sidelobe level, and therefore at a different flux, and time-dependent or antenna dependent gains can result as the azimuthally asymmetric sidelobes rotate over the source and pointing errors result in sidelobe jitter.
The ultimate solution to this problem lies in the direction-dependent gain solver, forthcoming in AIPS++ but not yet available, so we must use other means. Simply using an outlier field in addition to the main image will not work, as the value of the primary beam at the location of the confusing source may well be zero. Within AIPS++ current capabilities, one can turn off the application of the primary beam with function Imager.setvp by putting argument dovp=F. Then image the confusing regions one field at a time, and subtract the modeled flux from each field's visibilities. The residual visibilities can then be mosaiced with one of the standard multi-field algorithms. The packaging is not ideal at this point and you have to do some adhoc processing with the Table tool (which is one of the strengths of AIPS++ - you can do this when you have to !).
Here is an example:
opos := dm.direction('J2000', '12h26m33.248000', # Outlier direction
'02d19m43.290000')
imgr.setvp(dovp=F) # Turn off application of primary beam
#
for (myfield in 1:25) { # For each field image outlier and create model
modelName := spaste('model', i)
#
imgr.setdata(fieldid=myfield)
imgr.setimage(nx=64, ny=64, stokes='I',
cellx=0.2, celly=0.2,
phasecenter=opos)
imgr.clean(threshold='0.001Jy', model=modelName, ...) # Image outlier
#
imgr.ft(model=modelName) # Overwrite MODEL_DATA column in MS
}
imgr.done();
# we are about to make an irreversible change in the MS (called MS.TABLE here)
# so you'd better have a copy MS somewhere!
tab := table("MS.TABLE", readonly=F) # Create table tool from MS
correctedvis := tab.getcol("CORRECTED_DATA") # Get corrected data
modelvis := tab.getcol("MODEL_DATA") # Get model data
correctedvis -:= modelvis # Subtract model
tab.putcol("CORRECTED_DATA", correctedvis) # Put subtracted data back in
tab.done();
These are discussed in the basic Imaging chapter of Getting Results.
Component Models are handled by the Componentlist tool.
The only difference in the mosaicing context (from single field imaging) is that the Component Model must be a true representation of the sky brightness. Any attenuation for primary beams is handled by Imager.
If you have a Component Model which has been attenuated by the primary beamm you can correct for that with the Imager.pb function.
imgr.make('empty')
imgr.pb('empty', operation='correct', incomps='cl.attenuated.sky',
outcomps='cl.sky')
Note that you need the input image so that Imager knows what telescope you are using so that it can get the correct model. Alternatively, if you have used Imager.setvp to set a Voltage pattern from an external table, it would use that.
The Componentlists are specified by their disk file names. (the arguments are not Componentlist tools).
When correcting for the effects of the primary beam to achieve an accurate and uniform flux scale across the image (i.e. by dividing by the primary beam in the case of a single field observation), the noise and errors at the edge of the mosaic sky coverage are amplified. The noise amplification distracts from the visual beauty of the image and may complicate the image's display and interpretation.
Sault et al (1996) endorse a different image plane weighting in the mosaicing which results in a constant noise level across the image, but has a variable flux scale.
In AIPS++ we have implemented an image plane weighting similar to Sault's scheme, but the noise goes to zero outside the region covered by the primary beams. The flux scale is position dependent, but it is flat over most of the mosaic sky coverage. The flux scale images can be created by setting the fluxscale argument in Imager's setmfcontrol function. Regions outside the multi-field primary beam pattern will have a zero value.
myimager.setmfcontrol(minpb=0.1, scaletype='SAULT', constpb=0.4, fluxscale='fluxscale.image');
In this example we set to use the Sault's scheme for image plane weighing.
{\tt minpb} is used to set upto what point we image in the primary beam (here upto 10\% of the peak. {\tt constpb} is used to determine upto where in each primary beam we will keep the noise uniform (here upto 40\% of the peak).
Routinely in single field deconvolution, only the inner quarter of an image is deconvolved so that the sidelobes from this region can be correctly subtracted from the entire image. However, in the multi-field case, such a restriction usually does not exist. The major cycles only deconvolve down to a certain level, fixed by the sidelobe characteristics of the PSF. After that, the exact subtraction of the deconvolved flux is carried out. Typically, the exact subtraction is performed by multiplying the brightness distribution by a field's primary beam, convolving by that field's exact PSF, multiplying by the primary beam again, and subtracting from the previous cycle's residual mosaic. The two primary beam multiplications ensure that the far out effects of the PSF, which will not be correct due to the full-image deconvolution, will not effect the model brightness distribution.
If no mask is used, we help the single field major cycle deconvolution algorithms out by creating a mask from the generalized primary beam pattern of all observed fields, with zero outside the outermost fields' primary beam main lobes. If you don't want this mask for some reason, you should supply your own mask image.
Apart from some rather esoteric details in the solution interval, self-calibration of multi-field data in AIPS++ is operationally identical to self-calibration of single-field data, but with function Imager.setvp activated.
The success of self-calibration is largely dependent on being able to get a reasonable model for the source brightness distribution over some range of Fourier spacings. Synthesis imaging lore emphasizes the uses of self-calibration when bright point sources dominate the emission, but there is no rule that prohibits the use of shorter baselines in self-calibration. In mosaicing, there will generally be much more signal to work with on the shorter baselines, but the extended structure to which these baselines are sensitive is more likely to suffer from imaging errors than the simple point-like sources, especially if total power data is either lacking or questionable quality. Self-calibration on mosaic images is still on open field.
Self-calibration for multi-field observations starts with a model image of the entire mosaiced region, presumably obtained from either the Imager.clean or Imager.mem functions. Then the Imager.setvp function must be run to turn on the primary beam application (it should already be on if you have just made your clean or mem image with this Imager tool). Then use the Imager.ft function to calculate the model visibilities, given by the Fourier transform of the model brightness distribution times the primary beam, for each field. Then proceed with self-calibration as usual with a Calibrater tool.
The solution interval can be longer or shorter than the time spent on each field. One must consider the variable emission in the different fields. If the solution interval is very short, some fields may not have enough signal for a good solution, and solution intervals and gain solutions might be calculated on a field-by-field basis. If some fields do not have much emission and a short solution interval is desired, it me be desirable to self-calibrate only on those fields with enough emission for a good self-calibration solution. If the solution interval is longer than the integration time per field, then the fields with more emission (and higher signal-to-noise ratio) will dominate the gain solution, helping along the fields with less emission.
The following script is nothing special, just making an interferometer-only mosaic image from the multi-field test measurementset which is distributed with AIPS++:
include 'imager.g'
# Generate MS and construct Imager tool
imagermaketestmfms(msfile='XCAS.ms')
imgr := imager('XCAS.ms')
# Use the first field as the image center
imgr.setimage(nx=256, ny=256, cellx="3arcsec",
celly="3arcsec", stokes="I", doshift=F,
mode="mfs", spwid=[1:2], fieldid=1, facets=1)
# Weight each field individually
for (myfield in [1:7]) {
imgr.setdata(fieldid=myfield)
imgr.weight(type="uniform")
}
# Use all the data for the mosaic
imgr.setdata(mode="none", nchan=1, start=1, step=1,
spwid=[1:2], fieldid=[1:7])
# Using the mosaic gridder that uses the FT of the pb as gridding function
imgr.setoptions(ftmachine='mosaic');
# Use the voltage pattern (primary beam)
imgr.setvp(dovp=T, usedefaultvp=T, dosquint=F);
# Make a MEM image (using mask image)
base := 'mem'
maskname:= spaste(base, '.mask')
modname := spaste(base, '.model')
imgname := spaste(base, '.image')
resname := spaste(base, '.resid')
scalename := spaste(base, '.scale')
reg1:=drm.box([70, 70,1,1], [185, 185, 1, 1]) # define region of image
imgr.regionmask(maskname, reg1) # make a mask image to limit search for flux
imgr.setmfcontrol(cyclefactor=3.0, cyclespeedup=20.0,
fluxscale=scalename)
imgr.mem(algorithm='mfentropy', niter=80, sigma='0.001Jy',
targetflux='10.0Jy', constrainflux=F,
displayprogress=T, fixed=F,
complist='', prior='',
mask=maskname,
model=modname,
image=imgname,
residual=resname)
# Make a multi-scale CLEAN image for comparison
base := 'msclean'
modname := spaste(base, '.model')
imgname := spaste(base, '.image')
resname := spaste(base, '.resid')
scalename := spaste(base, '.scale')
imgr.setscales(scalemethod='uservector', uservector=[0.0, 3.0, 10.0, 20.0])
### please note the use of parameter stoplargenegatives
### which is set to false to let multiscale clean to continue despite hitting
### a negative on the largest scale
imgr.setmfcontrol(cyclefactor=3.0, stoplargenegatives=F,
fluxscale=scalename);
imgr.clean(algorithm='mfmultiscale', niter=1000, gain=0.6,
threshold='0Jy',
displayprogress=T, fixed=F, complist='',
mask=maskname,
model=modname,
image=imgname,
residual=resname)
# Destroy Imager tool
imgr.done();