
 News News |
 FAQ FAQ
|
 Search Search
|
 Home Home
|
| Getting Started | Documentation | Glish | Learn More | Programming | Contact Us |

| Version 1.9 Build 1556 |
|
The Jones matrices in equation 3 generally do not commute, so their order is important. In principle, the matrices must be placed in the `physical' order, i.e. the order of the signal propagation path. But in the equations that are enshrined in existing reduction packages, this is often not the case. This begs the question why these `wrong' equations seem to produce so many good (even spectacular) results. The question is especially important since a different order often results in considerable gains in computational efficiency.
The answer is that, for existing (arrays of) circularly symmetric parabolic feeds, many Jones matrices can be approximated by matrices that do commute with at least some of the others.
We will analyse this in terms of those special matrices (see Appendix for their definition), whose commutation properties are:
In order to study the general implications of changing the order of multiplication, we take the two products m.M and M.m of two general matrices (whose elements may be complex):
The difference (i.e. commutation error) between the two matrix
products can be expressed as a matrix ![]() :
:
Thus, by taking the wrong matrix order, one makes the following fractional errors of the following order in the result:
- in the diagonal elements: of the order of c/a, i.e. the ratio
of non-diagonal and diagonal elements of the original matrices (which
is often small).
- in the off-diagonal elements: in the order of (a - b)/a,
i.e. they will be smaller as the diagonal elements of the original
matrices are more equal.
If one of the two matrices is diagonal, e.g. c = d = 0 then this reduces to:
The (not very surprising) conclusion is that the error caused by taking the wrong matrix order is smaller when one of the matrices is diagonal, and the values of its diagonal elements are almsot equal.
It is sufficient to discuss the commutation properties of the
feed-based Jones matrices because, if
A![]() commutes with
B
commutes with
B![]() and
A
and
A![]() with
B
with
B![]() , then
(A
, then
(A![]()
![]() A
A![]() * )
commutes with
(B
* )
commutes with
(B![]()
![]() B
B![]() * ):
* ):
Inspecting the various Jones matrices separately:
= pure rotation
(
)
= diagonal matrix
(expi
, exp-i
)
,
= multiplication
(
)
= multiplication
(expi
.
) if
=
(virtually always the case)
= pure rotation
(
) if
=
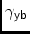
= diagonal matrix
(expi
, exp-i
) if
=
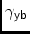
= pseudo-rotation
(
,
) if
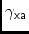
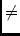
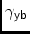
= A general matrix if
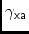
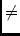
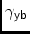
,
= diagonal matrix
(
,
) if no cross-leakage (
=
= 0)
= multiplication(
) if also
=
for all
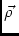
,
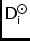
unit matrix
if small leakage, i.e. (

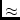

0)
=
(
,
)
(
,
)
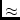
(
, -
)
(
) if
= -
and
=
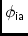
= (
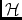
(
,
)
-1) (
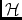
(
,
)
-1)
(
)
(expi
, exp-i
) if
= -
and
=
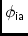
[] = anti-diagonal matrix: a problem, if present....
[] = effectively hidden if present, see equation 24
= diagonal matrix
(
,
) if no cross-talk
Problems are caused predominantly by matrices with non-zero
off-diagonal elements like
![]() ,
,
![]() , and
, and
![]() if
if
![]()
![]()
![]() . Of these, only
. Of these, only
![]() is
present in all telescopes.
is
present in all telescopes.
![]() will be a problem for SKAI,
bacause
will be a problem for SKAI,
bacause
![]()
![]()
![]() .
.
The following changes in the order of Jones matrices is allowed, but only under the indicated conditions. NB: Some Jones matrices will commute if it can be assumed that the observed source is compact, dominating, unpolarised and near the centre of the field. This is often the case.
The Jones matrices may split up in two groups:
![]() =
= ![]()
![]() . In these terms, the
full M.E. (ignoring normalisation factors, see equ
6) becomes:
. In these terms, the
full M.E. (ignoring normalisation factors, see equ
6) becomes:
We now see the reason for placing the integration over ![]() and
and
![]() to the left of the sum over k sources. Since it is
computationally advantageous to minimise the number of Jones matrices
that operate in the image plane, it must be investigated whether Jones
matrices that do not depend on the source position can be moved to the
left in the chain, using the rules in section 6.3
above. Depending on the chosen coordinate system, (and always
keeping in mind the conditions for re-ordering Jones matrices), the
following split appears to be the maximum obtainable:
to the left of the sum over k sources. Since it is
computationally advantageous to minimise the number of Jones matrices
that operate in the image plane, it must be investigated whether Jones
matrices that do not depend on the source position can be moved to the
left in the chain, using the rules in section 6.3
above. Depending on the chosen coordinate system, (and always
keeping in mind the conditions for re-ordering Jones matrices), the
following split appears to be the maximum obtainable:
This is what is done implicitly in some existing reduction packages.
For a tied array (ignoring integration and weight factors for the moment), equation 5 becomes:
Under extremely favourable conditions, i.e. if:
- individual feed beams per tied array are identical.
- Faraday rotation is the same for an entire tied array
- All receptors of a tied array have the same orientation.
- receptor cross-leakages are small.
- tied array feed signals are corrected before adding.
- there are no delay errors.
then equation 53 can be reduced to: