 News |
FAQ
|
| Search
|
Home
|
| Getting Started | Documentation | Glish | Learn More | Programming | Contact Us |
|
| Version 1.8 Build 235 |
|
Contributors: George Moellenbrock, Debra Shepherd,
Athol Kemball, &
the NRAO AIPS++ user group
Version: 2002 June
This document describes how to calibrate and image VLA data using the Astronomical Information Processing System (AIPS++). AIPS++ is a versatile suite of astronomical data reduction tools that can be run via mouse-based Graphical User Interfaces (GUIs) or an interactive command language called Glish.
For fairly standard VLA continuum and spectral-line observations (including polarimetry), this document can stand on its own. Additional AIPS++ documentation consists of:
For complicated images or unconventional observing strategies, it may be necessary to consult the more detailed AIPS++ documentation listed above. AIPS-aips++ and MIRIAD-aips++ dictionaries are also available which provide mapping of common AIPS and MIRIAD tasks/adverbs to their counterparts in AIPS++.
The data reduction categories covered in this document are those for continuum data, continuum polarimetry, spectral-line data, and spectral-line polarimetry. Individual steps in each data reduction sequence are illustrated using Glish script excerpts. These data reduction steps can equivalently be executed from the GUI interface.
AIPS++ is a tool-based reduction package. This means that related functionality are gathered into entities called `tools'. The user creates a working version of particular tool by logically associating a dataset with it, and giving the tool (data + functionality) a name. The different capabilities of this tool are then accessed by running one or more functions within that tool. For example, the basic pattern of usage is as follows:
mytool:=sometool(data='mydata'); # Create a tool of type sometool
# and call it mytool
mytool.functionA(param1=1,param2='a'); # Execute functionA of sometool,
# specifying parameters
mytool.functionG(); # Execute functionG of sometool,
# with no parameters
mytool.done(); # End use of tool
In this example, a tool of type `sometool' is created by associating it with a dataset (`mydata'), and giving it a name ('mytool'). Two different functions are executed in the tool using commands of the form toolname.function(parameters). All tools have a `done' function which undoes the explicit association of the tool functionality and the data.
Some tools have functionality which does not require that an explicit working version of the tool be created. Such functionality is accessed via `global functions'.
The reduction sequences given below use the following AIPS++ tools:
Visibility data in AIPS++ are stored in an AIPS++ table known as a MeasurementSet (MS). An MS consists of a main table containing the visibility data and associated sub-tables containing auxiliary or secondary information. The full MS data format is described in AIPS++ Note 229. Tables 1 & 2 identify the commonly accessed components of the MAIN table and list data selection parameters used during typical data reduction sessions.
All AIPS++ data files, including MeasurementSets, are written into the current working directory by default, with each AIPS++ Table represented as a separate sub-directory. MS names therefore need only comply with UNIX file or directory naming conventions, and can be referred to from within AIPS++ directly, or via full pathnames.
Each row of the DATA column in the MS contains a matrix of observed complex visibilities at a single time stamp, for a single baseline in a single spectral window. The shape of the data matrix is given by the number of channels and the number of correlations (voltage-products) formed by the backend instrument of the telescope (e.g. a correlator for an array, or a spectrometer for a single dish).
| Name | Format
 |
Comments |
| DATA | Complex(Nc, Nf) | Complex visibility matrix |
| Observed DATA for synthesis arrays | ||
| WEIGHT | Float(Nc) | Weight for whole data matrix |
| FLAG | Bool(Nc, Nf*) | Cumulative data flags |
| CORRECTED_DATA | Complex(Nc, Nf) | Corrected data created by calibrater or imager tools |
| MODEL_DATA
|
Complex(Nc, Nf) | Model data created by calibrater or imager tools |
| IMAGING_WEIGHT | Float(Nc) | Imaging weight, e.g. uniform, natural, robust |
| Created by calibrater or imager tools |
Additional data attributes are described in AIPS++
Note 229
Nc= number of correlators,
Nf= number of frequency channels.
The MODEL_DATA column is created
with each value having AMP = 1 & phase = 0o.
| Parameter | Contents |
| ANTENNA1 | First antenna in baseline |
| ANTENNA2 | Second antenna in baseline |
| FIELD_ID | Field (source no.) identification |
| SPECTRAL_WINDOW_ID | Spectral window number (IF no.) |
| ARRAY_ID | Subarray number |
| OBSERVATION_ID | Observation identification |
| POLARIZATION_ID | Polarization identification |
| SCAN_NUMBER | Scan number |
| TIME | Integration midpoint time |
| UVW | UVW coordinates |
Selection of data from an MS currently appears in different
guises in the various synthesis tools due to independent development
of these tools. An effort to reconcile these differences is underway.
This section assumes that AIPS++ has been installed on your UNIX or LINUX system. First, create a .aipsrc file in your home directory which will set some defaults and optimize run time. See Getting Started for a description of how to set up your .aipsrc file. An example .aipsrc file is given in Appendix 1.
To start AIPS++, cd to the directory you want to work in and type in an xterm window:
source /aips++/stable/aipsinit.csh # source the aipsinit.csh file
# that specifies setup parameters
aips++ # start aips++ (stable version)
You should get a Glish command prompt in the xterm window, a Tool Manager GUI window, and a Logger GUI window (see figure, above).
Check with your system administrator if you cannot locate the aipsinit.csh file.
It is also convenient to start up a viewer tool to view and analyze images easily. To start the default viewer GUI from the Glish command line type:
include 'viewer.g'; dv.gui();
Or, to start the default viewer from the tool manager window click on the Tools in use button. Select the viewer tool in the list and then the Show button. You will get a Data Manager tool which you can use to select any image and a viewer Display Panel:
You can put these off to the side until you are ready to use them. Note: once the aipsinit.csh file has been sourced, you can start the viewer directly from the UNIX prompt by typing viewer.
The remainder of this document uses Glish script sequences to execute data reduction steps. The Glish sequences can also be used as a guide for operation using the Tool Manager GUI interface. All parameter names and settings correspond exactly to those listed in the GUI interface (in general, only the immediately relevant parameters are listed in the glish sequences; others may be safely left set to default values). Consult the Getting Started document for general tips on the use of the Tool Manager.
An important difference between working with the GUI interface and the Glish command line interface is that a Glish command to run a task or function begins with all values set to their default values. Thus, the user need only specify values that will be changed from their defaults. However, the GUIs remember the state of each input. Thus, if you change an input, it will be remembered the next time you use the GUI. If you are unsure of the default value for a parameter in a GUI window, use the ``Wrench'' icon to the right of the input line to reset the value to its default. Also, GUI inputs do not require quotes around inputs while Glish does.
Note: From the Tool Manager window, you can click on Options: 'Copy commands to scripter' and Options: 'Show scripter' to write equivalent Glish commands of your GUI-based actions to a Scripter GUI window. This is useful because you can copy Glish script into a file and use this as a record of your data reduction session (or just save the Scripter commands directly with the 'Save' button at the bottom of the Scripter GUI). You can also modify scripts to reduce similar data in a semi-automated fashion.
When working from the Glish command line in AIPS++, basic tools for VLA data reduction and imaging must be initialized first. Type at the Glish command prompt:
include 'vlafiller.g'; # if filling from the VLA archive include 'ms.g'; # if filling from a UVFITS file include 'flagger.g'; include 'imager.g'; include 'msplot.g'; include 'calibrater.g'; include 'image.g'; include 'imagepol.g'; include 'viewer.g';
This is not required when working entirely from the GUI interface because the tools are loaded automatically when they are selected.
What happens if something goes wrong?
First, check that your inputs are correct. If you are working with the GUI interface, there is 'pop-up' help available on most inputs - simply put the cursor on an item and a short help statement will pop-up on the screen.
You can get help from the Tool Manager window by clicking on the 'Help' button and choosing the 'Reference Manual' option. This will drive your browser to the AIPS++ detailed documentation on each tool. From this web page, you can also reach the main AIPS++ documentation site (click on Documentation in the upper left of the web page) or you can run a Search on key words you are interested in.
Also, you can get help on each tool and the tool inputs by clicking on the 'Help' button in the GUI tool screen.
If your inputs are correct and you are still having problems, you may have discovered a software bug. If you find a bug during your data reduction session, type at the Glish command line prompt:
bug()
Or, using the Tool Manager 'Help' button, choose 'Report a bug'
option. This will bring up a bug report GUI that you can fill in and
submit automatically within AIPS++.
If you manage to find yourself in a hung state (don't worry, this is rare), you can kill AIPS++ from the LINIX or UNIX command line with:
LINUX: ps -aux | grep aips++
UNIX: ps -aef | grep aips++
Note the process ID numbers listed and kill them with the command:
kill -9 process_id
You are now ready to restart AIPS++.
Calibration and imaging responsibilities are divided between the calibrater and imager tools. The calibrater tool handles visibility-plane calibration while the imager tool deals with image formation, deconvolution and image-plane calibration.
In a typical synthesis observation, a number of calibrators of known structure (usually point sources, and at least one of known flux density) are observed in addition to the scientific target(s) in order to obtain a measure of the systematic properties of the instrument and, if relevant, the corrupting media above it. The effects of these systematic properties are then removed from the data for the scientific target. This technique is often referred to as cross-calibration and its success depends implicitly on the relationship between: 1) the true brightness distribution of the observed radio sources (what we are after); 2) the formal response of the instrument and its variety of imperfections of varying importance (what we are calibrating); 3) and the data that is actually recorded (what we have measured).
The AIPS++ Measurement Equation, originally defined by Hamaker, Bregman, & Sault (1996a, 1996b), is an explicit description of this relationship. The Measurement Equation (in the visibility plane) for a spectral line polarization calibration is given by
 = Bij Gij Dij Pij Tij 
|
(1.1) |
where:
= cross-correlations between two polarizations
for each of two feeds (i, j) which characterize an individual
baseline (e.g. the measured visibilities).
= visibilities measured by an ideal
interferometer (e.g. no instrumental errors or calibration effects).
= is directly related to the Fourier
Transform of the true polarized sky brightness,
= (I, Q, U, V).
Note that the Measurement Equation is a matrix equation.
and
are 4-vectors with
elements for each correlator product, and the Tij, etc., are
4x4 matrices that `corrupt' the correlator products according
to the properties of the specific term. The order of the corrupting
terms from right-to-left, for the most part, is the order in which the
errors affect the incoming wavefront. AIPS++ hardwires the
Measurement Equation order and all of the specific algebra associated
with the individual terms. As such, it is usually possible to ignore
the fact that the Measurement Equation is a matrix equation, and treat
the different terms as labeled `components' (black boxes) along the
signal path.
In practical calibration, it is often best to begin the calibration process by determining solutions for those terms which affect the data most. Thus, the user would normally determine gain solutions (G) first (applying pre-computed parallactic angle corrections P if doing polarization calibration), then bandpass solutions (B) and/or polarization solutions (D). Errors which are polarization-independent (T) can be determined at any point in the calibration process. T has nearly identical form to G but it located at a different point in the Measurement Equation. A practical advantage to this factorization is the ability to store polarization-independent effects which are characterized by a certain timescale or a particular parametrization (e.g., tropospheric opacity) as a separate calibration factor, thus isolating them from electronic gain effects which may vary on a different timescale and/or with different systematics. Although most data reduction sequences will probably proceed in this order, the user has complete freedom and flexibility to determine the order in which calibration effects are solved for. Self-calibration, the process by which an improved model of the target source is used to obtain improved solutions for the calibration, is also not limited to just the electronic gain (G) corrections, as has been traditionally the case. Improved solutions for, say, the instrumental polarization (D) may be obtained by self-calibration as well. In general, decision-making along the calibration path is a process of determining which effects are dominating the errors in the data and deciding how best to converge upon the optimal set of calibration solutions (for all relevant components) and source models which best describe the observed data.
Once the calibration solutions have been determined, the AIPS++ software applies the solutions according to the order defined by the Measurement Equation. The individual calibration components represented in the Measurement Equation are described in detail in the Synthesis Calibration chapter of Getting Results. The generalization of the Measurement Equation to image plane effects is also described there.
The observed data,
, are stored in the DATA column in
the MAIN table of the MS; these are the raw data as loaded by the
filler tool or imported from a UVFITS file. Associated with the DATA
column are related columns to hold the most recent version of the
calibrated data (CORRECTED_DATA), and the latest visibility plane
representation of the source or field model,
,
(MODEL_DATA). The latter two columns are filled in by the
calibrater and imagertools,
respectively. The actual calibration information is stored in
separate calibration tables. The observed DATA column does not
change during reduction, but the related columns do. When plotting
the data using a tool such as msplot, the data
sub-types (observed, corrected, and model) can be selected
individually.
Listed below are the basic steps for typical continuum and spectral line data reduction sessions which solve for and apply the standard complex gain (G), the polarization leakage (D), and the relative bandpass (B).
Since reduction of continuum, spectral-line, and polarimetry data in AIPS++ differ essentially only in the addition or omission of specific steps, and in the details of a few parameter settings, only one pass through the basic reduction path is described here. In the remainder of this document, annotated sequences of glish for both continuum polarimetry and spectral-line reduction are included in parallel. Some actions apply to only one type of reduction, but all methods are instructive for either type of observation.
The basic reduction sequence is:
Keep in mind that these examples are basic ones. More sophisticated sequences are possible. For example, it may be desirable to obtain bandpass calibration from an optimum calibrator, and to apply this on-the-fly during full-out G calibration on a different calibrator. This operation can be performed in the G and B calibrations steps listed above for the bandpass calibrator only, then repeating the G calibration step for the other calibrators with the B calibration applied. In fact, any sequence of operations of this nature is possible; the fundamental requirement is that calibration components that significantly influence the one being solved for be applied prior to the solution.
The two sample datasets used in the examples below are available from the AIPS++ Data Repository. The Data Repository is usually created in the directory /aips+ +/data/ when AIPS++ is installed on a UNIX or LINUX machine (check with your AIPS++ system administrator if the data are not here). You can create AIPS++ MeasurementSets from this data directly as described below using the ms tool.
The Glish sequences listed below describe calibration and imaging steps and are available as full end-to-end scripts in the AIPS++ Recipe Repository. Scripts in the Repository can be easily modified to reduce and image similar data sets.
The continuum polarimetry dataset is a full-polarization, VLA A-configuration observation at 5 GHz (one spectral window) of the gravitational lens 0957+561. A nearby point-like calibrator (0917+624) has been observed alternately with the target source. 3C286 is used for both flux density scaling and instrumental polarization calibration. The Glish script is available here: continuum polarimetry.
The spectral-line dataset is a short VLA D-configuration observation of HI (redshifed to 1413 MHz) in NGC5921. This dataset was observed in total intensity only (RR & LL), with 63 channels in a single spectral window. A nearby phase calibrator (1445+099) was observed, as well as 3C286 for flux density calibration. The Glish script is available here: spectral line.
For clarity in distinguishing operations for each of the sample datasets, tools associated with the continuum polarimetry reduction have names ending in `C' (imgrC, calC, etc.), and those associated with the spectral-line reduction have names ending in `S' (imgrS, calS, etc.).
There are two paths for importing VLA data into AIPS++: directly from a VLA archive or distribution tape, or from a UVFITS disk file generated by the AIPS task FITTP. Both methods are described here. The example data sets from the Data Repository are UVFITS files that have been created using the AIPS task FITTP.
VLA data in on-line archive format are read into AIPS++ from disk or tape using the vlafiller tool. Tape drives can be located on the local system or on a remote system accessible on the network. Use of a remote tape drive requires knowledge of the network host name (e.g. gibbon.cv.nrao.edu, or gibbon), and the tape device name (e.g. /dev/rmt/0ln). This can often be determined from the physical drive itself, or by logging on to the remote host and using a UNIX utility such as sysinfo or the UNIX command ls -lut /dev/r[ms]t* to list the device name.
Remote tapes need not be explicitly mounted from AIPS++ as the vlafiller itself will be run on the remote system directly. If you encounter problems in using the filler on a remote host, make sure that the AIPS++ initialization command source /aips++/release/aipsinit.csh is included in your .cshrc file (or the sh equivalent).
To run the vlafiller using a local tape drive, use the vlafillerfromtape global function, e.g.:
vlafillerfromtape(msname='cals00feb.ms', # Load project TESTT from tape to
device='/dev/rmt/0ln', # MeasurementSet cals00feb.ms
files=[2,3], # Read only file 2 and 3 on tape
project='TESTT'); # in current directory
To run the vlafiller using a remote tape drive:
vlafillerfromtape(msname='/home/cals00feb.ms', # Load project TESTT from remote
device='/dev/rmt/0ln', # tape on host 'gibbon' to MS
files=[2,3], # Read only file 2 and 3 on tape
project='TESTT', # cals00feb.ms in /home directory
host='gibbon'); # on remote host
Note that it is necessary to specify a full path name (recognizable by the remote host) for the output file when filling from a remote tape drive.
The vlafiller tool allows selection on frequency band, calibrator name, frequency range, project, time, subarray and source, and supports concatenation to an existing uv-data set.
It is usually desirable to obtain a summary of the dataset's properties after filling. This can be done by constructing an ms tool, and running the ms.summary function as follows:
mset:=ms(filename='cals00feb.ms'); # Construct the ms tool for the data mset.summary(verbose=T); # Write a summary to the logger window mset.done(); # Finish ms tool
Copy the summary information into a file for later use (source or FIELD_ID numbers and the times different sources are observed are particularly useful).
Data which have been exported to a disk file from AIPS using the task FITTP can be read into AIPS++ using the general UVFITS filler ms.fitstoms, which itself creates an ms tool. This is achieved as follows:
msetC:=fitstoms(msfile='ap366.ms',
fitsfile='/aips++/data/demo/AP366-09C1.fits');
# Construct the ms tool for
# the Continuum data set located
# in the AIPS++ Data Repository
msetC.summary(verbose=T); # Write a summary to the logger window
msetC.done(); # Finish ms tool
The detailed summary of the example data set is given in Appendix 2 for reference.
msetS:=fitstoms(msfile='ngc5921.ms',
fitsfile='/aips++/data/demo/NGC5921.fits');
# Construct the ms tool for
# the spectral line data set located
# in the AIPS++ Data Repository
msetS.summary(verbose=T); # Obtain summary
msetS.done(); # Finish ms tool
The detailed summary of the example data set is given in Appendix 2 for reference.
Once the data have been filled to a MeasurementSet, they can be examined or displayed using various tools. The Catalog tool provides an overview of AIPS++ data files at the highest level, as individual AIPS++ tables of different types (e.g. images, MS, etc) in a given directory. The Catalog tool can be started from Glish as:
include 'catalog.g' dc.gui()
Here, dc is the default catalog tool. It can also be accessed via the Toolmanager interface from the Tools in Use button. A mouse click on an individual MS listed in the catalog GUI followed by a click on the Summary button, will write a summary of the data in the MS to the logger (including frequency and polarization settings and fieldnames). This information is useful during calibration.
When you click on the View button (to view the presently selected catalog item) you will launch the tablebrowser which provides facilities to browse and examine all data fields in the MS main and sub-tables.
Note that indices in the MS, such as FIELD_ID, are stored as integers beginning with zero when viewed at the low level provided by the tablebrowser. All AIPS++ synthesis tools correct for this artifact of c+ + and present selection of indices beginning at one.
The primary graphical visibility data visualization tool in AIPS++ at present is msplot. msplot allows line and raster plots of the observed, corrected, and model data against a range of MS indices and parameters, as well as associated plots such as uv-coverage. Facilities are provided to support versatile data selection, range setting and plot iteration. Interactive editing is also supported, as described in the next section. It can be started from Glish via:
include 'msplot.g'
p := msplot(msfile='data.ms',
edit=T); # Allow editing as well as inspection
This will launch a gui for plot type and data selection. It can also be launched from the toolmanager via the Synthesis package, and ms module.
Consult the msplot documentation for more information on using this tool.
Command-based, interactive and automated editing capabilities are supported in the flagger tool.
To start the flagger tool, type the following:
fg:= flagger(msfile='mydata.ms') # start the flagger tool
The flagger tool offers several directed editing (flagging) operations. In general, this involves selecting the data to be flagged (based in indices, timeranges, etc.), then running a flagging operation. The flagging commands all have the option to run them on a trial basis. To flag data from antenna=5, spw=1, field=2, within a timerange:
fg.setantennas(ants=5) # Select data including antenna 5
fg.setids(spectralwindowid=1,fieldid=2) # Select spectral id and field id
fg.settimerange(starttime="24-FEB-2000/10:00:05", # Select timerange
endtime="24-FEB-2000/10:09:37");
fg.state(); # Review data selection
fg.flag(trial=T); # Trial run to see how many rows
# will be flagged
fg.flag(); # Flag it
To reset the data selection, type:
fg.reset();
To flag data from baseline 3-4, spw=2, field=1, within 
10s of a
timestamp:
fg.setbaselines(ants=[3,4]) # Select data for baseline 3-4
fg.setids(spectralwindowid=2,fieldid=1) # Select spectral id and field id
fg.settime(centertime="24-FEB-2000/10:00:05", # Select time and range
delta="10s");
fg.state(); # Review data selection
fg.flag(); # Flag it
The logic in the data selection options is as follows. The two time-related data selection options (set by flagger.settimerange and flagger.settime) are logically OR'd together, and the two antenna-related data selection options (set by flagger.setantennas and flagger.setbaselines are also logically OR'd. The net time selections, net antenna selections, and all other selections are then AND'd together. Note that the data selection persists after the flagging operation flagger.flag is executed. To clear the selection, execute the flagger.reset function, or execute individual selection commands without arguments to clear only that particular selection. For example, to flag all data to antenna 11 for the same spectral window, field, and timestamp as for baseline 3-4 above:
fg.setbaselines(); # Clears baseline selection fg.setantennas(ants=11); # Select antenna 11 fg.state(); # Review data selection fg.flag(); # Flag it
To unflag data based on a selection, use the flagger.unflag function. For example, to restore data for baseline 11-15 (that was flagged above):
fg.setantennas(); # Clears antenna selection
fg.setbaselines(ants=[11,15]); # Select baseline 11-15
fg.state(); # Review data selection (note
# other selections still in
# effect)
fg.unflag(); # undo previous flags
Note that use of flagger.unflag may restore data that had been flagged by other means (e.g., by the on-line system, or by other criteria in previous use of flagger or msplot). In the near future, a flexible means of manipulating flagging versions will be made available in AIPS++.
Consult the flagger tool documentation for more information on the details of data selection.
Several simple heuristic editing methods are available in the flagger tool. These methods act on the data selected as described above, but add an additional heuristic constraint.
For example, it is usually desirable to flag the auto-correlation data from the VLA (otherwise, the imager tool may attempt to use it in image formation as if it were single dish data). To do this:
fg.reset(); # Reset the data selection fg.flagac(); # Flag the auto-correlations
It is often the case that the VLA data near the beginning of scans (e.g. after field or frequency band changes is bad. To flag such data, use the flagger.quack function. For example, to remove 20 seconds of data at the beginning of scans (defined by gaps larger than 30 seconds) on field 3:
fg.reset(); # Reset the data selection
fg.setids(fieldid=3); # Limit quack to fieldid=3 only
fg.quack(scaninterval='30s', # Trial run of quack
delta='20s',
trial=T);
fg.quack(scaninterval='30s', # Quack it
delta='20s');
Automated editing methods are available in the flagger and autoflag tools. These include clipping, median flagging and related methods.
For example, to clip data outside of a specified amplitude range with the flagger tool:
fg.setids(fieldid=2, spwid=[1,2]); # Select field, spw
fg.setpol(pol=[1,4]); # Select polarizations 1,4
# (e.g., RR and LL)
fg.filter(column='DATA', # Flag data if, DATA column
operation='range', # Amplitudes are outside
comparison='Amplitude', # 1.12-1.34
range=['1.12Jy','1.34Jy'],
fullpol=T, # Extend flags to pols and
fullchan=T); # and chans that weren't
# tested
The autoflag tool has more sophisticated algorithms. Examples of its use will be included here in the near future.
To finish the flagger tool:
fg.done(); # Done with flagging
Interactive editing is possible on almost all graphical views of the data which are possible in msplot. To enable the editing option, it is necessary to set parameter edit=T when the msplot tool is created. The current set of flags will be saved (for possible restoration later). Select and plot data as in non-editing mode, then draw boxes with the left mouse button to select regions to flag and press the Flag button to flag it. As many flag boxes as desired may be drawn before executing the flags. Use the Locate button to obtain a listing (in the logger) of the data points within the box(es). Note that the listing may be very long if the region selected covers a large number of visibility points.
At this writing the channel and polarization flagging scope selections in msplot will only work if you have elected to plot all channels and/or polarization. This constraint will be relaxed in the near future.
Raster displays of visibility data are possible also, and maybe useful for spectral line data editing.
When solving for visibility-plane calibration components, the calibrater tool compares the observed DATA column with the MODEL_DATA column. The first time that an imager or calibrater tool is constructed for a given MS, the MODEL_DATA column is created and initialized with unit point source flux density visibilities (unpolarized) for all sources (e.g. AMP=1, phase=0o). The Imager.setjy function can then be used to set the proper flux density for flux density calibrators. For sources that are recognized flux density calibrators (listed below), Imager.setjy will calculate the Perley-Taylor (1999) flux densities, Fourier transform the data (trivially) and write the results to the MODEL_DATA column. For the VLA, the default source models are customarily point sources defined by the Baars or Perley-Taylor flux density scales, or point sources of unit flux density if the flux density is unknown. The MODEL_DATA column can also be filled with a model generated from an image of the source (e.g. the Fourier transform of an image generated after initial calibration of the data).
| Recognized Flux Density Calibrators | ||
| 3C Name | B1950 Name | J2000 Name |
| 3C286 | 1328+307 | 1331+305 |
| 3C48 | 0134+329 | 0137+331 |
| 3C147 | 0538+498 | 0542+498 |
| 3C138 | 0518+165 | 0521+166 |
| - - | 1934-638 | - - |
| 3C295 | 1409+524 | 1411+522 |
Set 3C286 (field 11) model according to Perley-Taylor (1999):
imgrC:=imager(filename='ap366.ms'); # Start imager tool
imgrC.setjy(fieldid=11); # Calculate & set flux density for
# 1328+307 (3C286)
Set 3C286 (field 1) model according to user-specified value (if you don't want to use the standard values):
imgrS:=imager(filename='ngc5921.ms'); # Start imager tool
imgrS.setjy(fieldid=1,
fluxdensity=[14.8009,0,0,0]);
# Set flux density of 1331+305
# (3C286) to 14.8009 Jy
At this point, the source model and observed data exist for all calibrators at all uv-points, and it is possible to begin solving for the gains.
It is almost invariably the case that the instrumental and atmospheric amplitude and phase gains (hereafter ``complex gains'') are the dominant calibration error in VLA data. Therefore we solve for this factor first.
For the standard cross-calibration scheme described here, only one term (G) will be used to describe the net complex gain (and so it will include atmospheric effects). One complex gain factor, as a function of time, will be determined for each field, spectral window, polarization, and antenna in the MS.
Note: Well-behaved antennas that are located near the center of the array are chosen as reference antennas for each dataset. For non-polarization datasets, reference antennas need not be specified although you can if you want to. If no reference antenna is specified, an effective phase reference that is an average over the data will be realized implicitly. For data that requires polarization calibration, it is important to choose a reference antenna that has a constant phase difference between the right and left polarizations (i.e., no phase jumps or drifts). If no reference antenna (or a poor one) is specified, the phase reference may have jumps in the R-L phase, and the resulting polarization position angle response will vary during the observation, thus corrupting the polarization imaging.
To solve for G, first choose a solution interval which samples the time scale over which you think the instrument or atmosphere is changing. Time scales depend on the array configuration and the observed frequency. Here, a time scale of 60 sec is chosen for the 6 cm continuum polarimetry data while 300 sec is chosen for the 21 cm spectral line data.
calC:=calibrater(filename='ap366.ms'); # Create Calibrater tool
calC.setdata(msselect='FIELD_ID IN [9,11]');
# Select calibrator sources
# in MS fields 9 & 11
calC.setapply(type='P', # Arrange to apply parallactic
t=5.0); # angle correction (for polarization
# only). Choose a 5 sec timescale.
# The P-table corrections are
# computed in AIPS++.
calC.setsolve(type='G', # Arrange to solve for G
t=60.0, # on a 60.0 sec timescale
refant=3, # Choose reference antenna 3:
table='ap366.gcal'); # a well-behaved antenna
# near the center of the array.
calC.state(); # Review setapply/setsolve settings
calC.solve(); # Solve for the net complex gains
# and write solutions to the table
# ap366.gcal located on disk.
calC.plotcal(tablename='ap366.gcal'); # Inspect solutions
Note that all calibrater.setapply and calibrater.setsolve executions prior to the calibrater.solve execution will be in effect when obtaining the solutions. Thus, the parallactic angle correction, P, is applied before the G solutions are obtained. The parallactic angle correction is required for polarimetry reduction, and may be omitted otherwise. If data imported from AIPS already had the parallactic angle correction applied using the AIPS task CLCOR, then the calibrater.setapply step for P should be omitted (it is the user's responsibility to keep track of this).
calS:=calibrater(filename='ngc5921.ms'); # Create calibrater tool for
# spectral line data set
calS.setdata(msselect='FIELD_ID <= 2', # Select data for calibrators
mode='channel', # (Fields 1 & 2)
start=3, # and drop the outer channels
nchan=55); # that may bias the gain solution.
calS.setsolve(type='G', # Arrange to solve for G on
t=300.0, # a 300-second timescale
refant=15, # Choose reference antenna 15:
table='ngc5921.gcal'); # a well-behaved antenna
# near the center of the array.
calS.state(); # Review setsolve settings
calS.solve(); # Solve for the net complex gains
# and write solutions to the table
# ngc5921.gcal located on disk.
calS.plotcal(tablename='ngc5921.gcal'); # Inspect solutions
Note that we have omitted application of P since there is no polarization data.
As illustrated above, the calibrater tool has three `set' functions (calibrater.setdata, calibrater.setapply, and calibrater.setsolve) and two `operational' functions (calibrater.solve and calibrater.correct). The calibrater.setdata function selects data and the calibrater.setapply and calibrater.setsolve functions set up the state of the calibrater tool. Both calibrater.setapply and calibrater.setsolve can be executed more than once (for different calibration components) prior to calibrater.solve or calibrater.correct (e.g., calibrater.setapply will typically be executed for both G and P before solving for D). Use the calibrater.state function to review the current state and the calibrater.reset function to clear all or part of the calibrater.setapply/calibrater.setsolve state.
The calibrater.solve function will apply the calibration components (specified with calibrater.setapply) to the observed DATA, and solve for the components specified with calibrater.setsolve. Note that is is possible to specify more than one component for solving. In this case, the solutions are done serially (not simultaneously) in the right-to-left order prescribed by the Measurement Equation formalism (e.g., G before D), with each newly-solved component applied before solving for the next (e.g., the obtained G solutions will be applied before solving for D).
The calibrater.correct function applies a set of calibrations to the observed data and saves it for imaging in the CORRECTED_DATA column of the MeasurementSet. Anything set by calibrater.setsolve is ignored by calibrater.correct.
In the case of spectral-line data, it is necessary to remove gain fluctuations that are a function of frequency. This is achieved by using the calibrater tool to solve for B calibration, in the present example, using 1331-305 as the bandpass calibrator. The G calibration obtained above is applied to ensure that the B calibration will be normalized. The solution interval is set very large so only one B solution (in time) is obtained.
calS.setdata(msselect='FIELD_ID==1'); # Select bandpass calibrator
# (Field 1 = 1331+305)
calS.reset(); # Reset apply/solve state
# of the calibrater tool
calS.setapply(type='G', # Arrange to apply G solutions
t=0.0, # from the table ngc5921.gcal
table='ngc5921.gcal');
calS.setsolve(type='B', # Arrange to solve for a single
t=86400.0, # bandpass solution for the
refant=15, # entire observation.
table='ngc5921.bcal');
calS.state(); # Review setapply/setsolve settings
calS.solve(); # Solve for the bandpass solutions
# and write them to the table
# ngc5921.bcal located on disk.
calS.plotcal(tablename='ngc5921.bcal', # Inspect the solutions
plottype='AMP',
multiplot=T);
For point sources of unknown flux density, but for which valid solutions have been derived against a unit point source model, the absolute flux density can be established by scaling the mean gain amplitudes against those of the known amplitude calibrators. This scaling is achieved using the calibrater.fluxscale function as follows:
calC.fluxscale(tablein='ap366.gcal', # Transfer the flux density scale
tableout='ap366.fluxcal', # from 1328+307 (B1950: 3C286)
reference='1328+307', # to the gain calibrator 0917+642.
transfer='0917+624'); # Write the solutions to
# the table ap366.fluxcal located
# on disk.
calC.plotcal(tablename='ap366.fluxcal'); # Inspect the solutions
calS.fluxscale(tablein='ngc5921.gcal', # Transfer the flux density scale
tableout='ngc5921.fluxcal', # from 1328+307 (J2000: 3C286)
reference='1331+30500002', # to the gain calibrator
transfer=['1445+09900002']); # 1445+09900002. Write the
# solutions to the table
# ngc5921.fluxcal located on disk.
calS.plotcal(tablename='ngc5921.fluxcal', # Inspect the solutions
plottype='AMP',
multiplot=F);
In both cases, the amplitude scale is set with 3C286 as the reference
flux density calibrator. The output calibration table contains the
scaled G calibration factors for all of the transfer sources, and
will be used in subsequent reduction steps. Proper scaling is
indicated in the calibrater.plotcal plots by smoothly varying (ideally
constant) amplitude gains for each antenna, despite source
changes. At high frequencies (
> 15 GHz), this scaling step may
be biased by elevation-dependent variation of the atmospheric
contribution to the system noise temperature. Methods for treating
this case properly will be available in the near future.
Before imaging, the data need to be corrected by applying the calibrations determined above. The calibrater.setdata function selects which data are to be corrected, and the calibrater.setapply function selects which solutions are to be applied. The calibrater.setapply function may be run several times (in any order) to specify simultaneous application of different calibration components. The components will be applied by the calibrater.correct function in the appropriate order according to the Measurement Equation. In AIPS++, calibration tables are always cumulative, and so are always applied to the observed data in the DATA column. The corrected data are written to the CORRECTED_DATA column in the MS, which will be used directly in imaging. Note: the observed DATA is NOT changed. If you want to change the solutions you have applied, simply create new calibration tables and correct the data again - the CORRECTED_DATA column will be over-written.
calC.setdata(msselect='FIELD_ID IN [9:11]'); # Select sources in MS fields
# 9, 10 & 11 to which calibration
# is to be applied
calC.reset(); # Reset setapply/setsolve
calC.setapply(type='P', # Arrange to apply parallactic angle
t=5.0); # correction on 5 sec intervals
calC.setapply(type='G', # Arrange to apply flux-scaled G
t=0.0, # solutions from the ap366.fluxcal
table='ap366.fluxcal'); # table.
calC.state(); # Review setapply settings
calC.correct(); # Apply solutions and write the
# CORRECTED_DATA column in the MS.
calS.setdata(msselect='FIELD_ID IN [2,3]'); # Select sources in MS fields
# 2, & 3 to which calibration
# is to be applied
calS.reset(); # Reset setapply/setsolve
calS.setapply(type='G', # Arrange to apply flux-scaled G
t=0.0, # solutions (from field 2) from
table='ngc5921.fluxcal', # the ngc5921.fluxcal table.
select='FIELD_ID==2');
calS.setapply(type='B', # Arrange to apply B solutions
t=0.0, # from the ngc5921.bcal table.
table='ngc5921.bcal',
select='');
calS.state(); # Review setapply settings
calS.correct(); # Apply solutions and write the
# CORRECTED_DATA column in the MS.
To calibrate field 1, as well, setdata(...) and setapply(type='G',...) should be executed again, selecting FIELD_ID==1 in both, followed by calibrater.correct.
At this point, the data for both continuum and spectral-line are sufficiently calibrated to attempt initial total intensity imaging.
For the case of continuum polarimetry, it is necessary to calibrate
the instrumental polarization (D) before high-quality polarization
images can be formed. Accurate D calibration depends on an
appropriate polarization model for the calibrator. If the
calibrator is unpolarized (Stokes Q = U 
0), and
point-like1.2, the simple total
intensity model (non-zero Stokes I only) used in the G calibration
is appropriate. In fact, the D calibration could have been obtained
at the same time as G by issuing an additional calibrater.setsolve execution before the solve was executed.
If the instrumental polarization calibrator is significantly polarized (as in the case of 3C286) a non-zero model for Stokes Q and U must be determined. This model can be obtained by imaging in polarization prior to D calibration, as described below. In the near future, a function for simply summing the polarization visibilities will be available to provide an initial polarization model estimate.
In this example, the polarization model of 3C286 is obtained by imaging the data after applying only the G (and P) calibration. Since 3C286 is virtually a point source at this frequency, the Stokes I, Q, and U values are obtained using the image.statistics function in the image tool. This operation is illustrated in the continuum polarimetry script.
The calibrater tool operations used in solving for D are similar to those used to solve for G. However, note that one additional parameter--preavg--is used explicitly in the calibrater.setsolve execution. Since only one D solution is desired for the entire observation, the solution interval is set very long, and the data for each baseline within the solution interval would nominally be averaged entirely before the solution is determined. However, the parallactic angle varies on timescales much shorter than the solution interval1.3. Thus, the preavg parameter is set to prevent averaging of the data beyond an acceptable timescale for the parallactic angle.
First make IQUV images of the polarization calibrator 3C286 to determine the polarization model (a more detailed description of imaging is given in the next section).
imgrC.setdata(mode='none', # Select continuum data for
fieldid=11); # for 3C286.
imgrC.setimage(nx=512, # Set up imaging parameters.
ny=512,
cellx='0.1arcsec',
celly='0.1arcsec',
stokes='IQUV',
fieldid=11);
imgrC.weight(type='uniform'); # Choose weighting
# e.g. uniform, natural.
imgrC.makeimage(type='corrected', # Make an image using the
image='3C286.cal1.im'); # CORRECTED_DATA column
# in the MS. Write the image
# 3C286.cal1.im to disk.
The resulting image, 3C286.cal1.im, written to disk, has 4 planes, with I, Q, U, and V images. Using the Viewer, obtain statistics on each plane of the IQUV image (see the Image Analysis section of this document for details about Viewer operation). Record the maximum OR minimum value, which ever has the largest absolute value. Use the viewer arrow buttons on the right to display Q and U images - record statistics for each image. Assume V = 0. Use the Stokes I value reported by the Imager.setjy function run earlier. For this example:
I = 7.462 Q = -0.621 U = -0.593 V = 0
If your data set has two spectral windows, create an image with spwid=2 and repeat this procedure to find I, Q, and U.
Now, solve for the D-term calibration:
stokes := [7.462, -0.621, -0.593, 0.0] # Define polarization model
# determined from imaging
imgrC.setjy(fieldid=11, # Set model for IQUV
fluxdensity=stokes);
calC.setdata(msselect='FIELD_ID==11'); # Select data for polarization
# calibrator, 3C286
calC.reset(); # Reset setapply/setsolve
calC.setapply(type='P', # Arrange to apply parallactic angle
t=5.0); # correction
calC.setapply(type='G', # Arrange to apply flux-scaled
t=0.0, # G solutions
table='ap366.fluxcal');
calC.setsolve(type='D', # Arrange to solve for D over a long
t=86400.0, # time scale, average data within
preavg=600.0, # the solution to no more than 600
table='ap366.dcal'); # sec per chunk.
# Write the solutions to the table
# ap366.dcal located on disk.
calC.state(); # Review setapply/setsolve settings
calC.solve(); # Solve
Examine the D-term or ``leakage'' solutions with the calibrater.plotcal function, with plottype='DRI' (D-term real versus imaginary components):
calC.plotcal(plottype="DRI" ,
tablename="ap366.dcal");
For VLA data like this example, see
http://www.aoc.nrao.edu/gtaylor/calman/polcal.html
for a description on how to plan for good polarization calibration and
what to expect when solving for D-terms.
Now, the data can be corrected for both G and D as follows:
calC.setdata(msselect='FIELD_ID IN [9:11]'); # Select fields 9, 10, & 11 to
# which calibration will be applied:
# 9 = gain calibrator 0917+642
# 10 = target source 0957+561
# 11 = polarization cal 3C286
calC.reset(); # Reset setapply/setsolve
calC.setapply(type='P', # Arrange to apply parallactic
t=5.0); # angle correction
calC.setapply(type='G', # Arrange to apply flux-scaled
t=0.0, # G solutions
table='ap366.fluxcal');
calC.setapply(type='D', # Arrange to apply D solutions
t=0.0,
table='ap366.dcal');
calC.state(); # review setapply settings
calC.correct() # Write the corrected the data
# to the CORRECTED_DATA column
# in the MS
The polarization calibration is almost complete - the final step, calibrating the electric vector position angle, will be done during the final imaging steps below.
Imaging is done using the imager tool, which supports a broad range of imaging modes and deconvolution algorithms, as described in the synthesis imaging chapter and in the User Reference Manual. This section describes single-field imaging/deconvolution for the continuum and spectral-line datasets using a CLEAN region which is defined interactively.
For the continuum dataset, make a single-field, full-polarization (I, Q, U, & V), continuum image of the target source, 0957+561. This image is made with the Clark CLEAN algorithm as follows:
First, use the imager.advise function to get an estimate of what the image properties should be. Then set the image parameters and weight, and CLEAN the image using an interactive cleaning algorithm:
imgrC.setdata(mode='none', # Select continuum data for the target
fieldid=10); # source in field 10 (0957+561)
imgrC.advise(takeadvice=F, # Determine image and cell size using
fieldofview='1arcmin'); # advise function. Do not take advice,
# note parameters in logger
# window and use as a basis for setimage.
# ADVISE FUNCTION RESULTS:
# Maximum uv distance = 585844 wavelengths
# Recommended cell size < 0.176041 arcsec
# Recommended number of pixels = 360
# Dispersion in uv, w distance = 293779, 94533.3 wavelengths
# Best fitting plane is w = 0.340419 * u + 0.340608 * v
# Dispersion in fitted w = 30797.4 wavelengths
# Wide field cleaning is not necessary
imgrC.setimage(nx=512, # Set image plane parameters
ny=512,
cellx='0.1arcsec',
celly='0.1arcsec',
stokes='IQUV', # (full polarization)
fieldid=10);
imgrC.weight(type='uniform'); # Set uniform weighting
At this point, you can examine the synthesized beam to determine the resolution resulting from the chosen weighting scheme and see what artifacts to expect from beam sidelobes during CLEANing, or you can proceed to CLEAN the image. To make an image of the synthesized beam (e.g. a PSF image):
imgrC.makeimage(type='psf', # Form the PSF image
image='0957+561.psf');
imgrC.fitpsf(psf='0957+561.psf'); # Measure the beam size
The beam size and position angle will be reported in the logger
window. To CLEAN the image:
imgrC.clean(algorithm='clark', # Image, and deconvolve using
niter=5000, # the Clark CLEAN
gain=0.1, # Write the cleaned image to the file
model='0957+561.mod', # 0957+561.im on disk.
image='0957+561.im',
residual='0957+561.resid',
mask='0957+561.mask', # Clean mask file name.
interactive=T, # Clean interactively, with the option
npercycle=500); # to choose a new clean region every
# 500 cleaning cycles.
During the CLEAN run, you will be asked to interactively define CLEAN regions (polygons or boxes) in a pop-up viewer. How to do this is described at the end of this section.
Note that the CLEAN component model is written as an image file. If necessary or desired, CLEANing may be restarted by specifying an existing (non-zero) model image, which will be subtracted before the deconvolution is resumed. This provides a simple means of monitoring progress of the deconvolution. Note that the imager.setdata and imager.setimage functions need not be run again when restarting a CLEAN with the previously setup imager tool.
When you are finished CLEANing, use the viewer to display the image
0957+561.im and obtain statistics.
The RMS should be
0.5 mJy beam-1.
The peak in the image is
26.2 mJy beam-1.
For the spectral-line dataset, total intensity images must be generated for NGC5921 for each spectral channel to form a spectral line cube. In this example, the CLEANing process is done on the line+continuum data and then the continuum is subtracted in the image plane.
Cleaning a spectral line cube with the continuum in each channel can be inefficient if most of the clean cycles are spent cleaning the same structure (e.g. continuum emission) in each plane. Thus, it is often better to subtract the continuum emission before the CLEAN process. A Glish script along with a description of how to do continuum subtraction in the uv plane, before imaging, will be available soon.
imgrS.setdata(mode='channel', # Select channel data for field 3
nchan=63,
start=1,
step=1,
fieldid=3);
imgrS.advise(takeadvice=F, # Determine image and cell size using
fieldofview='60arcmin'); # advise function. Do not take advice,
# note parameters in logger
# window and use for setimage.
# ADVISE FUNCTION RESULTS:
# Maximum uv distance = 4798.4 wavelengths
# Recommended cell size < 21.4931 arcsec
# Recommended number of pixels = 180
# Dispersion in uv, w distance = 1858.4, 759.892 wavelengths
# Best fitting plane is w = -0.253496 * u + -0.574818 * v
# Dispersion in fitted w = 172.198 wavelengths
# Wide field cleaning is not necessary
imgrS.setimage(nx=256, # Imaging parameters
ny=256,
cellx='10arcsec',
celly='10arcsec',
stokes='I',
mode='channel',
start=1,
step=1,
nchan=63,
fieldid=3);
imgrS.weight(type='uniform'); # Uniform weighting
or
imgrS.weight(type='briggs', # Robust weighting
rmode='norm',
robust=0.5);
At this point, you can examine the synthesized beam to see if you are happy with the resolution resulting from the chosen weighting scheme and see what artifacts to expect from beam sidelobes during CLEANing, or you can proceed to CLEAN the image.
To make an image of the synthesized beam (e.g. a PSF image):
imgrS.makeimage(type='psf', # Form the PSF image
image='ngc5921.psf');
imgrS.fitpsf(psf='ngc5921.psf'); # Measure the beam size
The beam size and position angle will be reported in the logger window.
To CLEAN the image:
imgrS.clean(algorithm='clark', # Image and deconvolve
niter=3000, # with Clark CLEAN
gain=0.1, # Write the cleaned image to the file
threshold='0Jy', # ngc5921.im on disk.
model='ngc5921.mod',
image='ngc5921.im',
residual='ngc5921.resid');
When you are finished CLEANing, use the Viewer to display the image
ngc5921.im and obtain statistics.
The RMS in each channel should be
1.7 mJy beam-1.
You should see 2 continuum source and the galaxy as you move through the cube. Note, in this example the entire inner quarter of the image is CLEANed. If desired, you can also use the interactive mask function as in the continuum polarimetry example.
Note: at this time, if you want to interactively define the CLEAN region or mask and then CLEAN down to a specified threshold level without continuing to set or change the mask, run CLEAN with niter set to a small number and interactive=T to define the mask. Then re-start CLEAN with niter set to a large number, threshold set to the level you want, mask set to your newly made mask, and interactive=F.
If you have sufficient signal-to-noise on your target source or any source in the field, then you may now use the calibrater tool to improve the dynamic range of your images. This improved calibration or "self-calibration" technique assumes that your images have been degraded by complex gain errors which vary too rapidly with time or direction to have been fully calibrated with the calibrator sources. The calibrater tool compares the observed uv DATA with a model of the data that you created during the initial CLEANing and determines amplitude and/or phase corrections which bring the CORRECTED_DATA into better agreement with the model.
Do not self-calibrate unless your target source has enough signal-to-noise to warrant improvement. Ask yourself whether your externally-calibrated CLEAN images contain artifacts well above the noise. If so, self-calibration may improve the image. If your images are limited by system noise, self-calibration may produce erroneous results, including the fabrication of weak sources!
Form the model using the imager tool and fill the MODEL_DATA column in the MS for target source:
imgrC.setdata(mode='none', # Select continuum data for the target
fieldid=10); # source in field 10 (0957+561)
imgrC.ft(model='0957+561.mod'); # Fill MODEL_DATA column in the MS
Now it is possible to determine new and improved calibration solutions. We want an incremental solution over the current G, so do an ``atmospheric phase'' T calibration (phase only, polarization-independent solutions):
calC.setdata(msselect='FIELD_ID==10'); # Set data for target source
calC.reset(); # Reset apply/solve state
calC.setapply(type='P', # Arrange to apply P corrections
t=5.0);
calC.setapply(type="G", # Arrange to apply flux-scaled
t=0, # G solutions
table="ap366.fluxcal");
calC.setapply(type="D", # Arrange to apply polarization
t=0, # D-term solutions
table="ap366.dcal");
calC.setsolve(type="T", # Arrange to solve for T to
t=10, # get an incremental solution to
preavg=0, # G with a phase-only correction.
phaseonly=T,
table="ap366.tcal");
calC.state(); # Review the setapply/setsolve settings
calC.solve(); # Solve for T
# Write the output to a table
# called ap366.tcal1 on disk
calC.plotcal(plottype="PHASE", # Examine solutions
tablename="ap366.tcal",
fields=10);
Now apply the P, G, D, and T solutions and write a new CORRECTED_DATA column for the target source in the MS:
calC.setapply(type="T", # Arrange to apply T solutions
t=0, # note: P, G, & D solutions are
table="ap366.tcal"); # already set to apply
calC.correct(); # Correct the data
CLEAN the self-calibrated image of 0957+561 to see how the self-calibration process improved the image:
imgrC.setdata(mode='none', # Select continuum data for the target
fieldid=10); # source in field 10 (0957+561)
imgrC.setimage(nx=512, # Set image plane parameters
ny=512,
cellx='0.1arcsec',
celly='0.1arcsec',
stokes='IQUV', # (full polarization)
fieldid=10);
imgrC.weight(type='uniform'); # Set uniform weighting
imgrC.clean(algorithm='clark', # Image, and deconvolve using
niter=5000, # the Clark CLEAN
gain=0.1, # Write the cleaned image to the file
model='0957+561.mod2', # 0957+561.im2 on disk.
image='0957+561.im2',
residual='0957+561.resid2',
mask='0957+561.mask2',
interactive=T, # Clean interactively, have the option
npercycle=500); # to choose a new clean region every
# 500 cleaning cycles.
Use the viewer to examine the final source image 0957+561.im2.
The RMS should be
0.24 mJy beam-1 (versus
0.5 mJy beam-1 before self-calibration). The peak in the image
is now
29.4 mJy beam-1 (versus 26.2 mJy beam-1 before
self-calibration). Self-calibration improved the dynamic range by a
factor of 2.3 in this example. Repeat the self-calibration as
necessary. Note: Self-calibration can be applied to any solvable
calibration component (G, and/or D in the present example).
In this example data set, there is an 80 mJy continuum source just south of the main line emission in NGC 5921. We can use this source to self-calibrate the line emission as shown below.
Create an image with line-free continuum channels only. First, create an image from line-free channels 5-8:
imgrS.setdata(mode='channel', # Select channel data for 4
nchan=4, # continuum-only channels in
start=5, # field 3 (target field)
step=1,
spwid=1,
fieldid=3);
imgrS.setimage(nx=256, # Imaging parameters
ny=256,
cellx='10arcsec',
celly='10arcsec',
stokes='I',
mode='channel', # Choose channel mode
start=5, # Grid selected channels into one.
step=4,
nchan=1,
spwid=1,
fieldid=3);
imgrS.weight(type='uniform'); # Uniform weighting
or
imgrS.weight(type='briggs', # Robust weighting
rmode='norm',
robust=0.5);
imgrS.clean(algorithm='clark', # Image and deconvolve
niter=1000, # with Clark CLEAN
gain=0.1, # Write the cleaned image,
threshold='0Jy', # ngc5921.c1.im and the model,
model='ngc5921.c1.mod', # image ngc5921.c1.mod to disk
image='ngc5921.c1.im',
residual='ngc5921.c1.resid');
Form the model using the imager tool and fill the MODEL_DATA column
in the MS for target source using only continuum channels that were
used to create the model:
imgrS.setdata(mode='channel', # Select channel data for 4
nchan=4, # continuum-only channels in
start=5, # field 3 (target field)
step=1,
spwid=1,
fieldid=3);
imgrS.ft(model='ngc5921.c1.mod'); # Fill MODEL_DATA column in the MS
We want an incremental solution over the current G, so do an ``atmospheric phase'' T calibration which will be derived from the continuum channels which were used to create the model (phase only, polarization-independent solutions): Note: the MODEL_DATA column is read automatically when solving for T. Set the time interval for the T solutions to be roughly the same as the solution intervals to get scan-based solution intervals.
calS.setdata(mode='channel', # Select channel data for 4
nchan=4, # continuum-only channels in
start=5, # field 3 (target field)
step=1,
msselect='FIELD_ID==3');
calS.reset(); # Reset apply/solve state
calS.setapply(type="G", # Arrange to apply flux-scaled
t=0, # G solutions
table="ngc5921.fluxcal");
calS.setapply(type="B", # Arrange to apply
t=0, # Bandpass solutions
table="ngc5921.bcal");
calS.setsolve(type="T", # Arrange to solve for T to
t=100, # get an incremental solution to
preavg=0, # G with a phase-only correction.
refant=15,
phaseonly=T, # Write the output to a table
table="ngc5921.tcal"); # called ngc5921.tcal on disk
calS.state(); # Review the setapply/setsolve settings
calS.solve(); # Solve for T
calS.plotcal(plottype="PHASE", # Examine solutions
tablename="ngc5921.tcal");
Now apply the G, B, and T solutions to all the data and write a new CORRECTED_DATA column for the target source in the MS:
calS.setdata(mode='channel', # Select channel data for 4
nchan=63, # continuum-only channels in
start=1, # field 3 (target field)
step=1,
msselect='FIELD_ID==3');
calS.reset(); # Reset apply/solve state
calS.setapply(type="G", # Arrange to apply flux-scaled
t=0, # G solutions
table="ngc5921.fluxcal");
calS.setapply(type="B", # Arrange to apply
t=0, # Bandpass solutions
table="ngc5921.bcal");
calS.setapply(type="T", # Arrange to apply T solutions
t=0,
table="ngc5921.tcal");
calS.correct(); # Correct the data
CLEAN the self-calibrated image of ngc5921 to see if the image is improved:
imgrS.setdata(mode='channel', # Select channel data for field 3
nchan=63,
start=1,
step=1,
fieldid=3)
imgrS.setimage(nx=256, # Select imaging parameters
ny=256,
cellx='10arcsec',
celly='10arcsec',
stokes='I',
mode='channel',
start=1,
step=1,
nchan=63,
fieldid=3);
imgrS.weight(type='uniform'); # Uniform weighting
or
imgrS.weight(type='briggs', # Robust weighting
rmode='norm',
robust=0.5);
imgrS.clean(algorithm='clark', # Image and deconvolve
niter=3000, # with Clark CLEAN
gain=0.1, # Write the cleaned image to the file
model='ngc5921.mod2', # ngc5921.im2 on disk.
image='ngc5921.im2',
residual='ngc5921.resid2'
Use the viewer to examine the final source image ngc5921.im2. The RMS
is
1.4 mJy beam-1 (versus 1.6 mJy beam-1 before
self-calibration). The peak of the continuum source is now
89.2 mJy beam-1 (versus 81.8 mJy beam-1 before
self-calibration). Thus, self-calibration provided a marginal
improvement to the image (the dynamic range improved by
20%).
If you have a data set in which there is a strong continuum source or strong line emission (e.g. a maser feature), and self-calibration improved the image significantly, then you can repeat the self-calibration as necessary. Note: Self-calibration can be applied to any solvable calibration component (G, T, and/or B in the present example).
Extensive display and image analysis tools are available in AIPS++. See the Display and Image analysis chapters of Getting Results for a detailed discussion on the options available. A brief orientation on the use of the Viewer is given below.
The Viewer
Start the viewer by typing at the Glish command prompt:
include 'viewer.g' dv.gui();
The viewer Data Manager and Display Panel GUIs will appear. Using the Data Manager, click on an image you would like to see in the Display Panel and choose the display type (e.g. Raster Image, Contour Map). The image will be loaded into the Display Panel. You can load as many images and display types as you want.
If you are using the GUI interface, you can also click on the ``Wrench'' icon from an image entry line in a tool window and select view to view a single image. The viewer is described in detail in the chapter on Display of Data while the 'Adjust' options are described at Adjust
To zoom in on a region, click on the 'zoom' button in the upper left of the Viewer display, use the left mouse button to make a region, double-click in the region to zoom. To un-zoom, hit the 'Unzoom' button at the bottom of the Display.
How the image, axes, and labels are displayed is controlled via the 'Adjustment' panel. Click on the 'Adjust' button to bring up this panel. There are a wide range of options to choose from: e.g. plot the beam, change the color map or stretch of an image, change contour lines, change the line width or color, add or delete labels. Once you have the image the way you like it, you can save the state of the image by clicking on the 'Save' button in the 'Adjustment' panel. The displaydata state can then be restored later by clicking on the 'Restore' button.
To obtain statistics on all or part of an image, click on the Tools: ImageAnalysis button at the top of the Viewer Display. An Image Analysis GUI will be created. Click on 'Statistics' to show the statistics panel. The 'Full' button will produce statistics on the full image (all planes). The 'Plane' button will produce statistics on only the region being displayed on the Viewer panel. Thus, to estimate the RMS in an image, zoom in on a region that has no emission and click on the Statistics panel 'Plane' button.
Use the 'DisplayData: Register' Panel to choose which images you want to register and display together. Use the 'DisplayData: Remove' Panel to delete images from the stack.
To print the image click on the 'Print' button at the bottom of the Viewer Panel. You will get a 'Canvas Print Manager' GUI to specify the output postscript file name or send the image to a local printer. Postscript files will be written to the directory you started AIPS++ in.
Below are straight-forward examples of a few image analysis tools that are useful for analyzing the example data sets:
Form a linear polarization intensity image, e.g.
P = 
and a vector image of the electric vectors of the polarization,
e.g. (Q + iU) as described in the Image
analysis chapters of Getting Results
impolC:=imagepol(infile="0957+561.im2"); # Start the image polarization tool
# for the image 0957+561.im2
linpolintC:=impolC.linpolint(); # Form linear polarization intensity
# image tool, linpolint
linpolintC.subim(outfile='0957+561.pint'); # Form the subim tool and write
# the image 0957+561.pint
# to a file on disk
subim.done(); # Close the tool (no longer needed)
linpolintC.done(); # Close the tool (no longer needed)
impol.complexlinpol(outfile="0957+561.cmplx");
# Create a vector image of the
# electric vectors of the polarization
impol.done(); # Close the tool (no longer needed)
Load the relevant images into the viewer tool using the Tool Manager window (that you created early in the session):
Bring up the 'Image Analysis' tool and determine the RMS of the
polarization intensity image using the 'Statistics' panel (for the
0957+561.im2 image, the RMS
1.5 x 10-4).
value yet. You will use this to set a mask expression in the
0957+561.cmplx vector image to get rid of polarization vectors that
are noise.
Click on the 'Adjust' button to bring up 3 Adjustment panels, one for each image. Then:
in the polarization intensity
image). Note, the name 0957+561.pint must be in quotes because it
contains a + sign which will be interpreted as an expression.
Now, calibrate the electric-vector positions angles, EVPA
= 0.5tan-1(U/Q) = 0.5*(R-L phase difference). First, it is
necessary to specify the true ratio U/Q found for the polarization
calibrator, 3C286. During the polarization calibration, we found for
3C286 (
I = 7.462 Q = - 0.621 U = - 0.593 V = 0), thus, the measured
R-L phase difference is:
tan-1(- 0.593/ - 0.621) = 0.762338001 radians
or
tan-1(- 0.593/ - 0.621)*180/
= 43.67875o. Since U and Q are
both negative, this is in the 3rd quadrant. Thus, the angle is
really
(- 180 + 43.68) = - 136.32o.
From the VLA calibration web page
(http://www.aoc.nrao.edu/
taylor/calman/polcal.html) we find the true
R-L phase difference for 3c286 is
66o. Thus, our phases
should be rotated by
66 - 136.32 = 70.32o or
EVPA = 0.5*70.32o. In the 'Adjust' panel for the 0957+561.cmplx
image, enter Extra rotation = 70.32/2. To plot the Magnetic field
vectors, enter Extra rotation =
70.32/2 + 90.
Create postscript files of the resulting images:
Now, use the image tool to subtract the continuum emission in the image plane using the line-free channels (5-8) and (55-58).
First, the image coordinate system is stored so that regions can be made in world coordinates. Then make two regions with the line-free emission and union them together. Note, a union of regions is a compound region that has to be made from two *world* regions, not pixel regions, so it must be constructed from regions made with the wrange function from the default regionmanager (drm). Once the line-free channels are unioned together, an integrated continuum image is made and subtracted from the line-cube.
imS:=image('ngc5921.im2'); # Start Image tool
cs:=imS.coordsys(); # Store image coordinate system
# in the variable 'cs'
range1:=dq.quantity([5,8],'pix');
# Create variable 'range1'
cont1:=drm.wrange(pixelaxis=4, # Make first region for lower
range=range1, # continuum channels,
csys=cs); # Pixelaxis 4 = frequency axis
range2:=dq.quantity([55,58],'pix');
# Create variable 'range2'
cont2:=drm.wrange(pixelaxis=4, # Make second region for upper
range=range2, # continuum channels,
csys=cs);
cont3:=drm.union(cont1,cont2); # Union the two chunks of data together
imS.moments(outfile='ngc5921.cont',
moments=-1, # Create an integrated
axis=4, # continuum image, ngc5921.cont,
region=cont3); # and write the file to disk.
nocont:=imagecalc(outfile='ngc5921.nocont',
pixels='ngc5921.im2 - ngc5921.cont');
# Subtract the continuum from the
# line cube and write the line-only
# cube, ngc5921.nocont, to disk.
imS.done(); # close the tool, no longer needed
cs.done(); # close the tool, no longer needed
nocont.done(); # close the tool, no longer needed
View the final image in the Viewer. The continuum sources should now be gone and you can see the rotation curve of the HI in the galaxy as you move through the line cube.
Now, take a spectrum through the cube. There are two ways to pick positions for taking spectra: 1) view the continuum image and take spectra at the locations of the continuum sources to make sure that continuum subtraction has gone OK; 2) view the 0th moment image (generated by the imageprofilefitter tool automatically) and use this to select spectra in regions with line emission. The latter is the default behavior. However spectral line cubes can have noisy beginning and end channels, so it is often better to view your own 0th moment image when selecting positions for spectra. Both of these ways are shown below:
Use the continuum image to check that the continuum subtraction has gone well.
include 'imageprofilefitter.g'; # Create image profile fitter tool
pf:=imageprofilefitter(infile='ngc5921.nocont',
infile2='ngc5921.cont');
# Get a spectrum from ngc5921.nocont
# But use the image of ngc5921.cont
# To see where to place the cursor
You will get a Viewer window labeled 'Image Profile Fitter' which shows the line+continuum image. To get a spectrum:
The spectrum below, taken at the position of the brightest continuum source, shows that the continuum subtraction appears to have done a good job - the spectrum is flat and amplitude is zero.
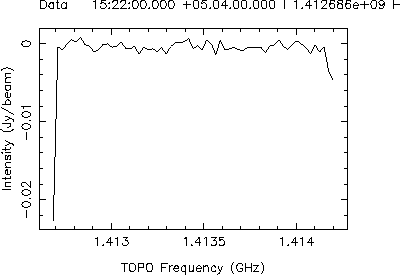
Create a line-only 0th moment image and use this to select regions of line emission to take spectra: Moment analysis for line-emission cubes. Viewing the image we find that there is line emission in channels 7-49.
imS:=image('ngc5921.nocont'); # Start Image tool
cs:=imS.coordsys(); # Store image coordinate system
line_range:=dq.quantity([7,49],'pix'); # There is line emission in
# channels 7-49
line_region:=drm.wrange(pixelaxis=4, # Define the line region in
range=line_range, # world coordinates
csys=cs);
imS.moments(moments=[0, 1, 2] ,
smoothaxes=[1,2,4] , # Pixels to be included in
# moment analysis will be
# decided by examing the
# flux in a smoothed version
# of the data.
# We will smooth in ra, dec
# and velocity (axis=1,2,4)
region = line_region, # Only use channels with
# line emission
mask='$imS>0', # Only include pixels with
# positive flux in original map
excludepix=[0.003], # Only sum flux from pixels
# in smoothed map with flux
# greater than abs(0.003 Jy)
smoothtypes="gauss gauss hann" ,# Gaussian smoothing in ra
# and dec; Hanning smoothing
smoothwidths=[5,5,3] , # Width of smoothing kernals
doppler="OPTICAL" , # optical velocity definition
outfile='ngc5921.nocont2');
The moments command will create 3 images:
ngc5921.nocont2.integrated # Moment 0 image
ngc5921.nocont2.weighted_coord # Moment 1 image
ngc5921.nocont2.weighted_dispersion_coord # Moment 2 image
Now take a spectra using the clipped, integrated image to isolate
the area of line-emission:
include 'imageprofilefitter.g';
pf2:=imageprofilefitter(infile='ngc5921.nocont',
infile2='ngc5921.nocont2.integrated');
The spectrum below, illustrating a classic double-peaked line profile
showing the galactic rotation, a was made with the 'Polygon-Region'
option in the Viewer window to circle the emission in NGC 5921, then
double clicking on the region to create the spectrum.
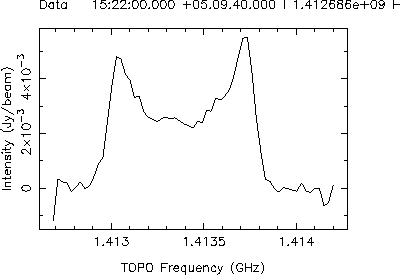
After completing work with AIPS++ tools, it is desirable to close them out by issuing the done function for each, as follows:
calC.done(); # Finish imager tool imgrC.done(); # Finish calibrater tool imC.done(); # Finish image tool
calS.done(); # Finish imager tool imgrS.done(); # Finish calibrater tool imS.done(); # Finish image tool
Hamaker, J.P., Bregman, J.D., and Sault, R.J., 1996a, A&AS, 117, 137.
Sault, R.J., Hamaker, J.P., and Bregman, J.D., 1996b, A&AS, 117, 149.
# # Work in the current directory: # user.aipsdir: . # # Put scratch files here: can be a list of directories # user.directories.work: /export/home/your_computer/aips++/scratch # # Put the aips++ cache files in one place: it shouldn't be # over an NFS mount or it will slow aips++ down to a crawl! # user.cache: /export/home/your_computer/aips++/cache # # Set these so that bug(), ask(), etc. know who you are # userinfo.name: Your_name userinfo.email: Your_email@institution.edu userinfo.org: Your Organization # # Switch on the display of memory used by each server # user.display.memory: True # # Uncomment this to send log messages to the deep blue yonder # #logger.file: none # # plot axis labels as the default in the viewer # and set initial character size (normal default size = 1.2): # display.axislabels: on display.axislabels.charsize: 1.2 # # system.aipscenter: NorthAmerica logger.file: aips++.log logger.height: 15 catalog.gui.auto: T catalog.confirm: T catalog.view.PostScript: ghostview toolmanager.gui.auto: T toolmanager.refresh: 10s
Detailed summary of the continuum polarimetry dataset (created with the command msetC.summary(verbose=T)):
MeasurementSet Name: ap366.ms MS Version 2
Observer: AP366 Project:
Observation: VLA
Data records: 93239 Total integration time = 21935 seconds
Observed from 22-May-1998/22:40:05 to 23-May-1998/04:45:40
ObservationID = 1 ArrayID = 1
Date Timerange Field DataDescIds
22-May-1998/22:40:05.0 - 22:41:10.0 0917+624 [1]
23:05:30.0 - 23:14:00.0 0957+561 [1]
23:26:55.0 - 23:47:30.0 0917+624 [1]
23-May-1998/00:10:50.0 - 00:18:20.0 0957+561 [1]
00:30:15.0 - 00:31:20.0 0917+624 [1]
00:53:15.0 - 04:45:40.0 1328+307 [1]
Fields: 3
ID Name Right Ascension Declination Epoch
9 0917+624 09:21:36.23 +62.15.52.18 J2000
10 0957+561 10:01:20.70 +55.53.52.65 J2000
11 1328+307 13:31:08.28 +30.30.32.94 J2000
Data descriptions: 1 (1 spectral windows and 1 polarization setups)
ID Ref.Freq #Chans Resolution TotalBW Correlations
1 4885.1 MHz 1 50000 kHz 50000 kHz RR RL LR LL
Feeds: 28: printing first row only
Antenna Spectral Window # Receptors Polarizations
1 -1 2 [ R, L]
Antennas: 27:
ID Name Station Diam. Long. Lat.
1 1 VLA:W16 25.0 m -107.37.57.4 +33.53.33.0
2 2 VLA:N16 25.0 m -107.37.10.9 +33.54.48.0
3 3 VLA:N48 25.0 m -107.37.38.1 +33.59.06.2
4 4 VLA:W8 25.0 m -107.37.21.6 +33.53.53.0
5 5 VLA:N56 25.0 m -107.37.47.9 +34.00.38.4
6 6 VLA:E16 25.0 m -107.36.09.8 +33.53.40.0
7 7 VLA:E24 25.0 m -107.35.13.4 +33.53.18.1
8 8 VLA:N8 25.0 m -107.37.07.5 +33.54.15.8
9 9 VLA:E8 25.0 m -107.36.48.9 +33.53.55.1
10 10 VLA:W40 25.0 m -107.41.13.5 +33.51.43.1
11 11 VLA:N24 25.0 m -107.37.16.1 +33.55.37.7
13 13 VLA:W56 25.0 m -107.44.26.7 +33.49.54.6
14 14 VLA:E64 25.0 m -107.27.00.1 +33.50.06.7
15 15 VLA:N64 25.0 m -107.37.58.7 +34.02.20.5
16 16 VLA:W32 25.0 m -107.39.54.8 +33.52.27.2
17 17 VLA:W64 25.0 m -107.46.20.1 +33.48.50.9
18 18 VLA:E48 25.0 m -107.30.56.1 +33.51.38.4
19 19 VLA:N40 25.0 m -107.37.29.5 +33.57.44.4
20 20 VLA:E40 25.0 m -107.32.35.4 +33.52.16.9
21 21 VLA:E56 25.0 m -107.29.04.1 +33.50.54.9
22 22 VLA:E72 25.0 m -107.24.42.3 +33.49.18.0
23 23 VLA:W24 25.0 m -107.38.49.0 +33.53.04.0
24 24 VLA:N32 25.0 m -107.37.22.0 +33.56.33.6
25 25 VLA:W72 25.0 m -107.48.24.0 +33.47.41.2
26 26 VLA:W48 25.0 m -107.42.44.3 +33.50.52.1
27 27 VLA:N72 25.0 m -107.38.10.5 +34.04.12.2
28 28 VLA:E32 25.0 m -107.34.01.5 +33.52.50.3
Tables:
MAIN 93239 rows
ANTENNA 28 rows
DATA_DESCRIPTION 1 row
DOPPLER <absent>
FEED 28 rows
FIELD 11 rows
FLAG_CMD <empty>
FREQ_OFFSET <absent>
HISTORY 108 rows
OBSERVATION 1 row
POINTING 168 rows
POLARIZATION 1 row
PROCESSOR <empty>
SOURCE <absent> (see FIELD)
SPECTRAL_WINDOW 1 row
STATE <empty>
SYSCAL <absent>
WEATHER <absent>
Detailed summary of the spectral line dataset (created with the command msetS.summary(verbose=T)):
MeasurementSet Name: ngc5921.ms MS Version 2
Observer: TEST Project:
Observation: VLA
Data records: 22653 Total integration time = 5280 seconds
Observed from 13-Apr-1995/09:19:00 to 13-Apr-1995/10:47:00
ObservationID = 1 ArrayID = 1
Date Timerange Field DataDescIds
13-Apr-1995/09:19:00.0 - 09:24:30.0 1331+30500002 [1]
09:27:30.0 - 09:29:30.0 1445+09900002 [1]
09:33:00.0 - 09:48:00.0 N5921 [1]
09:50:30.0 - 10:23:00.0 1445+09900002 [1]
10:26:00.0 - 10:43:00.0 N5921 [1]
10:45:30.0 - 10:47:00.0 1445+09900002 [1]
Fields: 3
ID Name Right Ascension Declination Epoch
1 1331+3050000213:31:08.29 +30.30.32.96 J2000
2 1445+0990000214:45:16.47 +09.58.36.07 J2000
3 N5921 15:22:00.00 +05.04.00.00 J2000
Data descriptions: 1 (1 spectral windows and 1 polarization setups)
ID Ref.Freq #Chans Resolution TotalBW Correlations
1 1413.45MHz 63 24.4141kHz 1550.2 kHz RR LL
Feeds: 28: printing first row only
Antenna Spectral Window # Receptors Polarizations
1 -1 2 [ R, L]
Antennas: 27:
ID Name Station Diam. Long. Lat.
1 1 VLA:N7 25.0 m -107.37.07.2 +33.54.12.9
2 2 VLA:W1 25.0 m -107.37.05.9 +33.54.00.5
3 3 VLA:W2 25.0 m -107.37.07.4 +33.54.00.9
4 4 VLA:E1 25.0 m -107.37.05.7 +33.53.59.2
5 5 VLA:E3 25.0 m -107.37.02.8 +33.54.00.5
6 6 VLA:E9 25.0 m -107.36.45.1 +33.53.53.6
7 7 VLA:E6 25.0 m -107.36.55.6 +33.53.57.7
8 8 VLA:W8 25.0 m -107.37.21.6 +33.53.53.0
9 9 VLA:N5 25.0 m -107.37.06.7 +33.54.08.0
10 10 VLA:W3 25.0 m -107.37.08.9 +33.54.00.1
11 11 VLA:N4 25.0 m -107.37.06.5 +33.54.06.1
12 12 VLA:W5 25.0 m -107.37.13.0 +33.53.57.8
13 13 VLA:N3 25.0 m -107.37.06.3 +33.54.04.8
14 14 VLA:N1 25.0 m -107.37.06.0 +33.54.01.8
15 15 VLA:N2 25.0 m -107.37.06.2 +33.54.03.5
16 16 VLA:E7 25.0 m -107.36.52.4 +33.53.56.5
17 17 VLA:E8 25.0 m -107.36.48.9 +33.53.55.1
18 18 VLA:W4 25.0 m -107.37.10.8 +33.53.59.1
19 19 VLA:E5 25.0 m -107.36.58.4 +33.53.58.8
20 20 VLA:W9 25.0 m -107.37.25.1 +33.53.51.0
21 21 VLA:W6 25.0 m -107.37.15.6 +33.53.56.4
22 22 VLA:E4 25.0 m -107.37.00.8 +33.53.59.7
24 24 VLA:E2 25.0 m -107.37.04.4 +33.54.01.1
25 25 VLA:N6 25.0 m -107.37.06.9 +33.54.10.3
26 26 VLA:N9 25.0 m -107.37.07.8 +33.54.19.0
27 27 VLA:N8 25.0 m -107.37.07.5 +33.54.15.8
28 28 VLA:W7 25.0 m -107.37.18.4 +33.53.54.8
Tables:
MAIN 22653 rows
ANTENNA 28 rows
DATA_DESCRIPTION 1 row
DOPPLER <absent>
FEED 28 rows
FIELD 3 rows
FLAG_CMD <empty>
FREQ_OFFSET <absent>
HISTORY 270 rows
OBSERVATION 1 row
POINTING 168 rows
POLARIZATION 1 row
PROCESSOR <empty>
SOURCE <absent> (see FIELD)
SPECTRAL_WINDOW 1 row
STATE <empty>
SYSCAL <absent>
WEATHER <absent>